17. 力 センサ
力 センサは、物体に加わる力やトルクを電気信号に変換するセンサで、ロボットや工作機械、自動車、医療機器など、さまざまな分野で広く使用されている。力 センサには、以下のような種類がある。
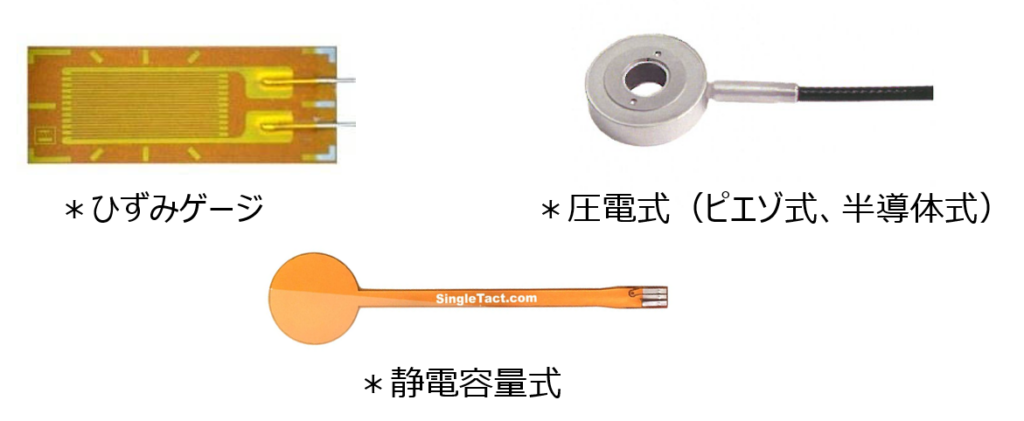
・ひずみゲージ式:金属箔、金属線などで構成されたひずみゲージに力が加わると、抵抗値が変化する性質を利用したセンサで、高精度で小型だが、温度変化の影響を受けやすい。
・圧電式(ピエゾ式、半導体式):機械的応力を受けると電荷を生成する物 質(圧電材料)を利用したセンサ、応答速度が速く、高温・高圧環境にも使用できるが、測定精度がひずみゲージ式に比べて低い。
・静電容量式: 2枚の電極の間に力が加わると静電容量が変化する性質を利用したセンサで、非接触で測定できるため、摩擦や摩耗がないという利点があるが、測定精度はひずみゲージ式や圧電式に比べて低い。
力 センサの例
図1に力 センサの外観例を示す。測定対象や測定環境に応じて様々な形状があり、求められる測定精度などに対して適切なセンサを選択することが重要である。
ひずみゲージの原理
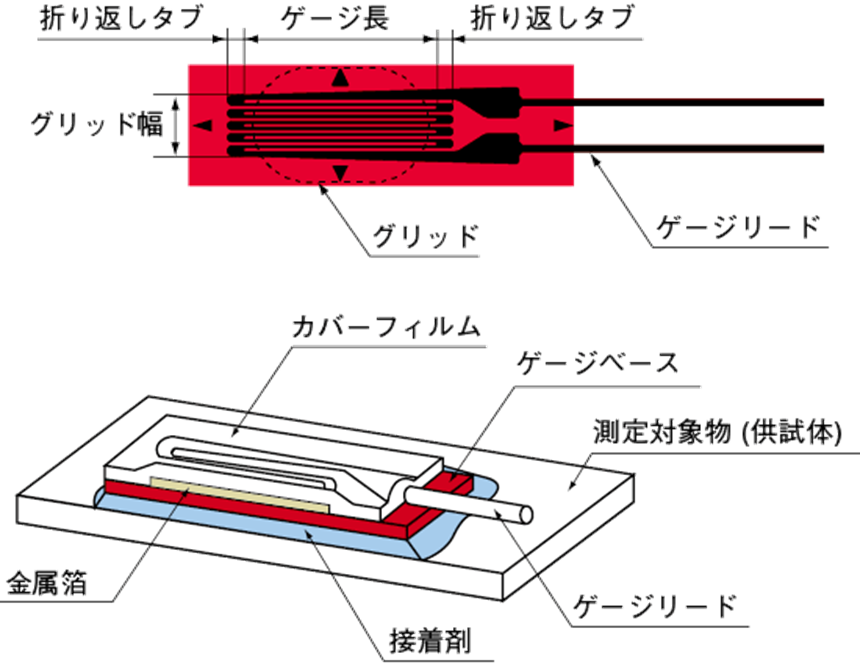
ひずみ(歪)とは、材料に加わる外力に比例して材料が伸びたり縮んだりする変形の量のことをいう。ひずみゲージは、図2(上)のようにフィルム状の薄い電気絶縁物の上に、格子上の抵抗線やフォトエッチング加工した抵抗箔を形成し、引出し線を付けた構造になっている。これを、図2(下)のように測定対象物(供試体)の表面に専用接着剤などで貼り付ける。これにより、測定対象物が外力でひずむと、ひずみゲージもひずむので、このひずみを測定すれば、測定対象物に掛かった外力が計測できる。
ひずみによる抵抗値の変化
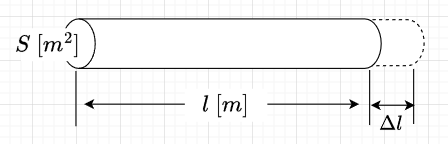
図1のような、長さ\(l\;[m]\) 、断面積\(S\;[m^2]\)、 抵抗率\(\rho\ [\Omega \cdot m]\)の金属線の抵抗値\(R\)は、$$R = \rho \frac{l}{s} \;[\Omega] \;\cdots (1)$$となる。
※抵抗率:材料の電気伝導のし難さを表す物性値。 電気伝導率(導電率:工学用語)\(\sigma\;[S/m]\)の逆数である。
金属の線(図1)で考えると、長さ \(l\) が \(\Delta l\) ほど長くなると、断面積\(S\) は\(\Delta S\)減ることになり、式(1)より、\(R\)は\(\Delta R\)増加する。従って、$$\frac{\Delta R}{R} \approx F \frac{\Delta l}{l}$$となる。ここで、\(F\)は比例係数でゲージ率(各ゲージ固有の係数)という。
※ゲージ率は、ひずみゲージの感度を表す係数。 一般のひずみゲージで使っている銅・ニッケル系やニッケル・クロム系合金のゲージ率は、約2である。
https://tml.jp/knowledge/strain_gauge/about.html
ひずみ
材料に引張力(または圧縮力)\(P\)が加わると、これに対する応力\(\sigma\)が材料内部に発生する。
この応力に比例して引張ひずみ(または圧縮ひずみ)が発生し、長さ\(L\)の材料は、\(L + \Delta L\)(または\(L -\Delta L\) )に変形する。このときの\(L\)と\(\Delta L\)の割合をひずみと言う。
*応力:物体に外力が加わった場合、それに応じて物体の内部に生じる力の大きさや作用方向を表現するために用いられる物理量のこと。物体内に発生している単位面積あたりの力で表す。応力が大きいと物体は変形、破壊に至る。
応力:\(\sigma\) 、引っ張る力:\(P\)、断面積:\(A\)とすると、$$ \sigma = \frac{P}{A}$$である。
抵抗値の変化測定
ブリッジ回路の使用が、ひずみゲージの抵抗値変化を測定する基本的な方式である。図4のブリッジ回路より、$$V_a = \frac{R_2}{R_1 + R_2}E \\ V_b = \frac{R_3}{R_4 + R_3}E \\ e = V_a - V_b$$である。初期状態として、\(R=R_1 = R_2 = R_3 = R_4\)とする。(ひずみゲージの抵抗値\(R_1\)に他の抵抗値を調整して合わせておく)このとき、\(V_a = V_b\)なので、\(e=0\)となる。
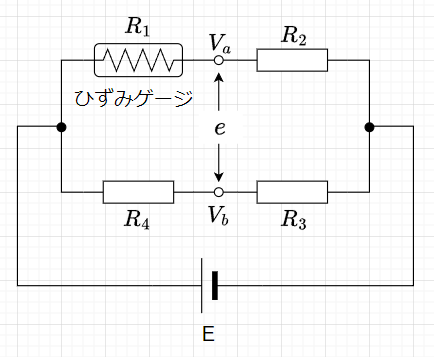
ひずみゲージの抵抗値が\(R_1 + \Delta R\)に変化すると、$$V_a = \frac{R_2}{R_1 + \Delta R +R_2}E=\frac{R}{2R + \Delta R}E ,\;\;\;\;V_b = \frac{R}{2R}E=\frac{1}{2}E \\e = V_b - V_a = \frac{1}{2}E- \frac{R}{2R + \Delta R}E = \frac{\Delta R}{4R + 2\Delta R}E \approx \frac{\Delta R}{4R}E ,\;\;\;\;\;(2\Delta R \ll 4R)$$となる。また、\(\frac{\Delta R}{R} = F \cdot \epsilon\) ,(\(\epsilon\):ひずみ、\(F\):ゲージ率) なので、出力電圧は、$$e = \frac{1}{4}F \cdot \epsilon \cdot E \;[V]$$である。従って、この出力電圧\(e\)から換算することで「力」を求めることができる。
圧電式 力 センサの原理
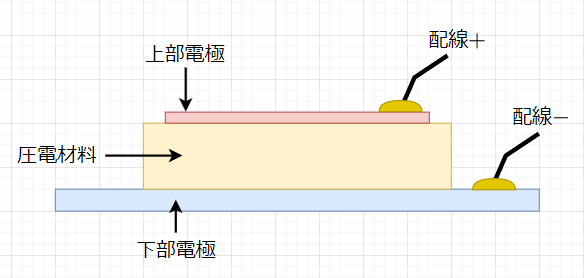
図5に圧電式 力 センサの構造を示す。電極間に圧電材料を挟み込んだ構造となっている。圧力(力)を加わると、圧力に比例した分極(表面電荷)が現れる現象(圧電効果)で得られた電荷をチャージアンプを用いて電圧信号に変換し、この電圧を力に換算して計測する。
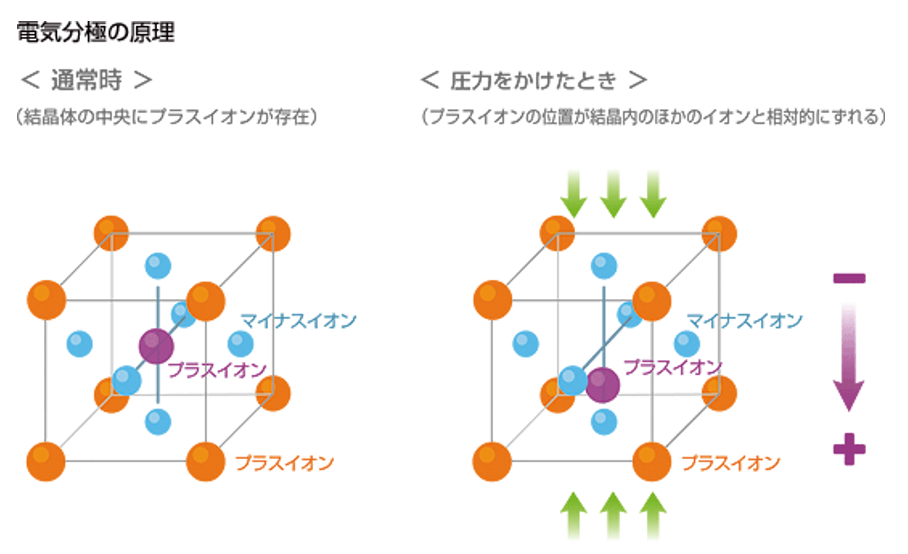
図6に電気分極の原理を示す。格子状の結晶の中に配置されたイオンの位置のずれが、圧力を加えることによって大きくなり、結晶の一方の端がプラスの電気を帯び、もう一方の端がマイナスの電気を帯びる「電気分極」という現象が起こり、電圧が発生する。
圧電効果・逆圧電効果
圧電効果( piezoelectric effect):物質(特に水晶や特定のセラミックス)に圧力(力)を加えると、圧力に比例した分極(表面電荷)が現れる現象。
逆圧電効果:電界を印加すると物質が変形する現象。
https://www.jp.tdk.com/tech-mag/knowledge/089
静電容量式 力 センサの原理
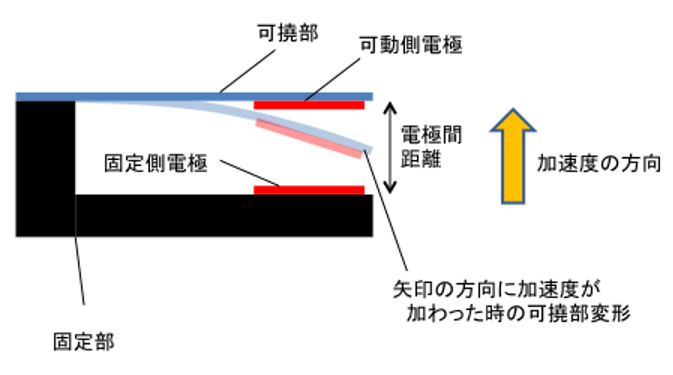
図7に静電容量型加速度センサの概念図を示す。静電容量型は、可撓部とある一定の間隔で、加速度によって変形しない固定部を設け、可撓部と固定部にそれぞれ電極を設ける構造となっている。変形(ひずみ)が発生すると2つの電極間距離が変化し、それによって電極間の「静電容量」が変化するので、この容量変化を検出することで、加速度が計測できる。なお、静電容量は式(1)で表せる。
$$C=\epsilon_0 \epsilon_r \frac{A}{d} \; \cdots \cdots (1)$$ \(C\;[F]\):静電容量、\(\epsilon_0\):真空の誘電率(定数)、\(\epsilon_r\):電極間の物資の比誘電率(通常は空気の誘電率)、\(A\):電極の面積、\(d\):電極間の距離
ひずみゲージ使用の実践
ひずみゲージ使用の実践に関しては、https://www.kyowa-ei.com/jpn/technical/strainbasic_course/index.html を参考にして下さい。以下に一部を引用する。
力 センサが測る量の範囲
力 センサが測る量の範囲は、0.1N~100N 程度のものが多い。例を表1に示す。
| 測定レンジ | 分解能(感度) |
| \(0.1\;N\) (\(100\; mN \approx 10\; gf\)) | \(20 \;\mu N\) (\(\approx 0.002gf\)) |
| \(1 \;N\) (\(\approx 100 \; gf\)) | \(0.1 \; mN\) (\(\approx 0.01gf\)) |
| \(5\; N\) (\(\approx 0.5 \;kgf\)) | \(0.5 \; mN\) (\(\approx 0.05gf\)) |
THKプレシジョン㈱ 型番FS1M-*** の場合
※\(kgf\)(キログラム重):重量キログラムとは質量が標準重力加速度のもとで受ける重力の大きさのこと。
\(1\;N = 1\; kg\cdot m/s^2\) \(1\;kgf = 9.80665\;N\)
つまり、体重計で量った\(1 \;kg\)の物(質量\(1 \; kg\))を持った時に感じる重さが \(1\;kgf \approx 9.8 \;N\)である。


“17. 力 センサ” に対して1件のコメントがあります。
コメントは受け付けていません。