19. 抵抗・インピーダンスの測定(1)
インピーダンスは、抵抗、キャパシタ(コンデンサ)、インダクタ(コイル)などの電気的性質を複素数で表したものである。インピーダンスの測定には、以下の2つの方法がある。
1.直流法:オームの法則に基づいてインピーダンスを測定する方法で、抵抗器両端の電圧と、回路に流れる電流を測定し、電圧を電流で割ることでインピーダンスを求める。直流法は、比較的簡単な方法であるが、測定対象が直流動作なので、測定対象のインピーダンスが抵抗のみの場合に使用できる。
2.交流法:交流法は、交流信号を用いてインピーダンスを測定する方法で、インピーダンス測定器で、インピーダンスの大きさと位相を測定する。交流法は、抵抗だけでなく、キャパシタやインダクタのインピーダンスも測定できる。また、直流法よりも、高い精度で測定できる。
インピーダンス測定器には、以下の種類がある。
・LCRメータ:抵抗、コンデンサ、インダクタのインピーダンスを測定できる。
・インピーダンスアナライザ:LCRメータの機能に加え、周波数特性やインピーダンスの複素平面表示など、より詳細な分析ができる。
抵抗値のおおよそを測定したい場合は、テスター(マルチメータ)が簡便である。テスターの内部構造や使用法に関しては、以下を参照願います。
・https://www.hioki.co.jp/jp/products/listUse/?category=42
・https://www.marutsu.co.jp/pc/static/large_order/mame/189
抵抗の測定
近年では、図1に示すような、高精度のディジタル抵抗計(高確度:0.1 mΩを0.16 %、分解能:0.01 μΩ)がある。従って、実際の抵抗測定では、簡易的にはテスター(ディジタルマルチメータ)、高精度が必要な場合にはディジタル抵抗計を使用するのが妥当である。しかし、測定の原理を知っておくことは重要なので、以下にまとめる。

https://www.hioki.co.jp/jp/products/detail/?product_key=467
中位抵抗の測定
電圧降下法
この方法は、測定対象の抵抗における電圧(電圧降下)\(V\)と電流\(I\)を測定し、オームの法則から抵抗\(R\)を間接計測する方法で、電圧降下法という。
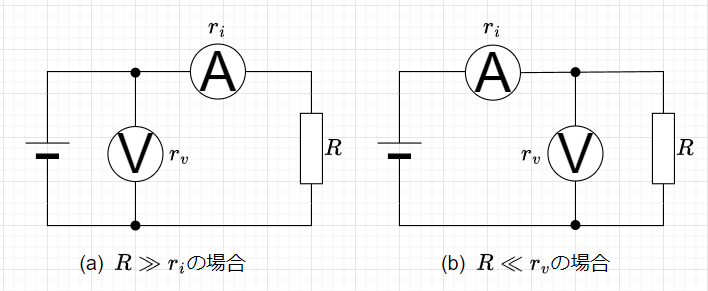
$$R = \frac{V}{I}$$で抵抗値を求める。この方法では、電圧計、電圧計の内部抵抗の影響を受けるため、測定対象の抵抗値の大きさによって、図2のように計器の接続法を変更する必要がある。図2(a)の測定対象の\(R\)の抵抗値が電流計の内部抵抗\(r_i\)より十分に大きい場合\(R \gg r_i\)、電流計を抵抗\(R\)側に接続する。このとき、電流計内部の電圧降下があるので、抵抗に流れる電流、つまり電流計の指示を\(I\)、電圧計の指示を\(V\)として、抵抗\(R\)の電圧降下\(V_R\)は、$$V_R = V - I r_i$$となる。従って、抵抗\(R\)は、$$R = \frac{V_R}{I} = \frac{V - I r_i}{I} \; \cdots (1)$$となる。図2(b)の測定対象の\(R\)の抵抗値が電圧計の内部抵抗\(r_v\)より十分に小さい場合\(R \ll r_v\)、電圧計を抵抗\(R\)側に接続する。このとき、抵抗\(R\)の電圧降下は電圧計の指示値\(V\)となるが、抵抗\(R\)に流れる電流\(I_R\)は、電流計の指示値\(I\)から電圧計の内部抵抗\(r_v\)に流れる電流を減じることになる。つまり、$$I_R = I - \frac{V}{r_v}$$となる。従って、抵抗\(R\)は、$$R = \frac{V}{I_R} = \frac{V}{I - \frac{V}{r_v}}\;\cdots (2)$$となる。式(1)を変形すると、$$\frac{V}{I} = R \left(1 + \frac{r_i}{R}\right)$$となる。この式から、\(R \gg r_i\)であれば、図2(a)の接続法で電圧計の指示値\(V\)と電流計の指示値\(I\)から算出する抵抗値\(R\)におよぼす影響は小さくなることがわかる。同様に、式(2)を変形すると、$$\frac{V}{I} = \frac{R}{1 + \frac{R}{r_v}}$$となる。この式から、\(R \ll r_v\)であれば、図1(b)の接続法で電圧計の指示値(V)と電流計の指示値(I)から算出する抵抗値(R)におよぼす影響は小さくなることがわかる。
ホイートストンブリッジ法
ホイートストンブリッジ法は、零位法の典型的な測定法である。図3のホイートストンブリッジにおいて、\(R_p,\;R_q,\;R_r\)を既知の抵抗器とする。また、\(R_x\)を測定対象の抵抗とする。検流器\(G\)に電流が流れないように、つまり平衡点となるように、\(R_p,\;R_q,\;R_r\)の抵抗器を調整する。平衡点では、$$R_p I_1 = R_q I_2 ,\;\;\;\;\;R_r I_1 = R_x I_2$$となるので、$$R_x = \frac{R_q}{R_p} R_r$$が求まる。
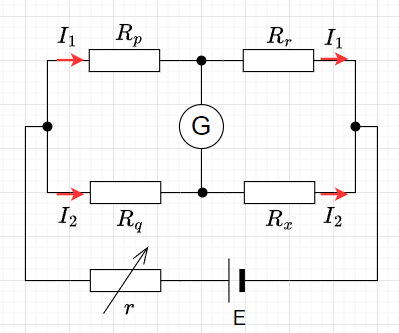
この式には、電源電圧\(E\)、可変抵抗\(r\)が入っていないことから、測定結果は電源電圧\(E\)の変動に影響されない。また、一般的には\(R_q,\;R_p\)には標準抵抗を使用して倍率を決め、\(R_r\)を調整して平衡点を見つけ、\(R_x\)を決定する。なお、可変抵抗器\(r\)は、ブリッジ回路に流れる全電流の調整に使われる。
低抵抗の測定
数\(m\Omega\)~数\(\Omega\)程度の低抵抗を測定する場合は、導線抵抗、接触抵抗、熱起電力、抵抗の温度特性などを考慮する必要がある。
電圧降下法
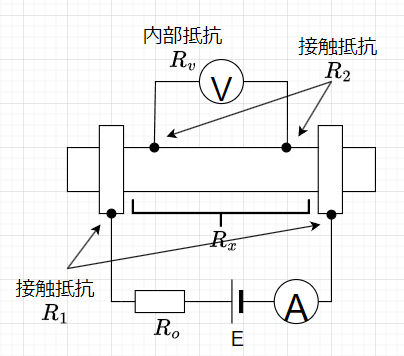
測定対象の低抵抗\(R_x\)を電圧降下法で計測する場合、電圧計、電流計との接触抵抗が問題となる。この場合、図4に示すように、電圧計用端子と電流計用端子を分離する。端子を分離することで、接触抵抗を\(R_1,\;R_2\)と見なせる。電圧計の内部抵抗\(R_v\)は\(R_2\)よりも十分に大きいので、\(R_2\)による電圧降下は無視できる。なお、\(R_x,\;R_o,\; R_1\)及び、電流計は直列に接続されているので、\(R_x\)に流れる電流値は、電流計の指示値である。また、測定対象\(R_x\)の抵抗値は小さいので、\(R_o\)により、電流を制限する。
ケルビンダブルブリッジ法
例えば、送電線の電線は良導体であるが、電気抵抗を測ってみるとわずかではあるが抵抗値を持つ。導体のような\(m \Omega\)単位の低抵抗を測定する場合、リード線の抵抗や接触抵抗の影響を受けない低抵抗測定器(ケルビンダブルブリッジ)を用いる。図5にケルビンダブルブリッジ回路を用いる。図5で\(R_x\)部分が測定対象の低抵抗体である。
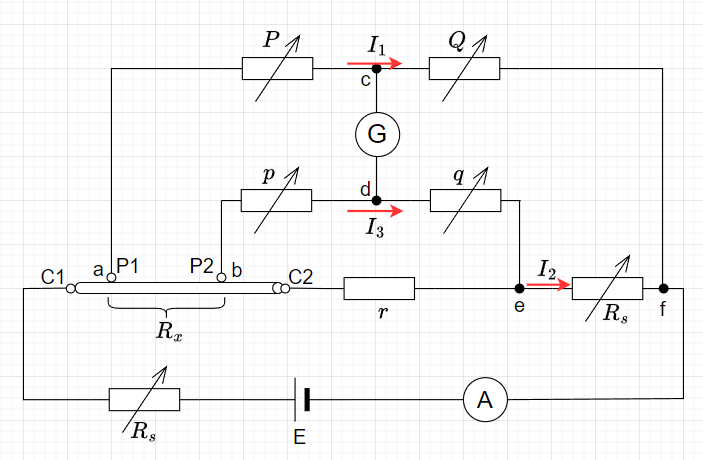
検流計\(G\)の振れがゼロになるように各可変抵抗\(P,\;Q,\;p,\;q\)を調整する。このとき、c-d間の電位差はゼロなので、c, dは同電位である。従って、a-c間の電圧降下とa-b-d間の電圧降下は等しいので、$$P I_1 = Rx I_2 + p I_3\; \cdots(1)$$である。また、c-f間の電圧降下とd-e-f間の電圧降下は等しいので、$$Q I_1 = q I_3 + R_s I_2\; \cdots(2)$$である。電流\(I_3\)は分流則により、$$I_3 = \frac{r}{p + q+ r} I_2 \; \cdots(3)$$となる。式(3)を式(1)、式(2)に代入して、整理すると$$P I_1 = I_2 \left(R_x + \frac{p r}{p + q + r} \right) \; \cdots(4) \\ Q I_1 = I_2 \left( R_s + \frac{q r}{p + q + r}\right) \; \cdots(5)$$となる。式(4)、式(5)の比をとると、$$\frac{P}{Q} = \frac{R_x + \frac{p r}{p + q + r}}{R_s + \frac{q r}{p + q + r}} \\R_x + \frac{p r}{p + q + r} = \frac{P}{Q}\left(R_s + \frac{q r}{p + q + r}\right) $$よって、$$R_x = \frac{P}{Q} \left(R_s + \frac{q r}{p + q + r}\right) - \frac{p r}{p + q + r} = \frac{P}{Q} R_s + \frac{q r}{p + q + r}\left(\frac{P}{Q} - \frac{p}{q}\right)$$である。ここで、\(\frac{P}{Q} = \frac{p}{q}\)のように\(P,\;Q,\;p,\;q\)は連動して変化する構造なので、\(\frac{P}{Q} - \frac{p}{q} = 0\)となり、測定対象の\(R_x\)は、$$R_x =\frac{P}{Q} R_s \; \cdots(6)$$と求まる。
測定する未知抵抗の値が数\(\Omega\)以下の抵抗測定の場合、普通は無視できる接続端子の接触抵抗やリード線の抵抗が未知抵抗に対して大きな割合を占めることになり、これが誤差となって正確な測定ができない。ダブルブリッジでは図5のように、測定対象\(R_x\)の接続は四端子構造にしてある。図5の回路において、P1 点、P2点のリード線抵抗と端子での接触抵抗 は、それぞれ抵抗\(P,\;p\) に含まれる。ダブルブリッジは抵抗の比、 \(\frac{P}{Q}\) や\(\frac{p}{q}\) が測定に関係するのであって、\(P,\;Q,\;p,\;q\) の各抵抗値はある程度自由 に選択できる。従って、\(P,\;p\)を比較的大きな抵抗値にしておけば、この中に含まれるリー ド線の抵抗や、端子の接触抵抗はほとんど無視できる。また、b-C2間のリード線抵抗は図に示す\(r\) の部分に含まれることになるが、ダブ ルブリッジでは、比例辺が\(\frac{P}{Q},\;\frac{p}{q}\) の二つあり、常に\(\frac{P}{Q} = \frac{p}{q}\) になる構造にしてある。したがって、\(R_x\)を求める式(6)からわかるように\(r\)は計算上消去されて、測定値には関係しないので、\(r\) にリード線抵抗が入っても問題ない。なお、C1-a 間のリード線抵抗は電源回路に入ってしまうので、誤差に関係しない。
電位差計法
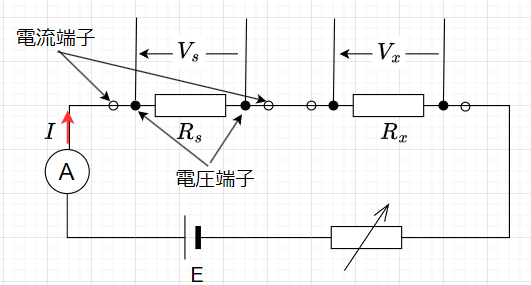
電位差計法では、図6のように標準抵抗\(R_s\)と測定対象の抵抗\(R_x\)を直列に接続し、電流\(I\)を流す。電位差計で、\(R_s\)、\(R_x\)の電圧降下\(V_s\)、\(V_x\)を測定する。\(V_s = I R_s\)、\(V_x = I R_x\)より、$$R_x = \frac{V_x}{V_s} R_s$$となるので、\(R_x\)の抵抗値が求まる。
四端子法による半導体の抵抗測定
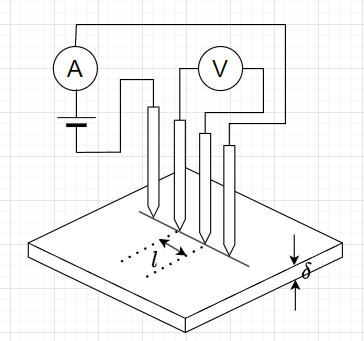
半導体の薄膜の抵抗率の測定には、4本の針を探針とした4端子測定を使う。図7にその概略を示す。4本の針を距離 \(l\) で等間隔に並べる。内側の2端子が電圧計測、外側が電流を流す端子である。これにより、接触抵抗の影響を小さくして、電圧\(V\)を測定できる。薄膜の厚さ\(\delta\)が\(l\)に対して十分小さい場合(\(\delta \ll l\))、導電率\(\sigma\)(抵抗率の逆数)は、$$\sigma =\frac{I \ln 2}{V \pi \delta} $$である。
また、薄膜の厚さ\(\delta\)が\(l\)に対して十分大きい場合(\(\delta \gg l\))、導電率\(\sigma\)は 、$$\sigma = \frac{I}{2 \pi l V}$$と近似できる。なお、四端子測定は電極の接触抵抗の影響は受け難いが、良好な計測を得るには、金属探針と半導体との接触抵抗を十分減らす工夫は必要である。
高抵抗の測定
数百\(k\Omega\)~数百\(M\Omega\)程度の高抵抗を測定する場合、十分な感度を得るために高電圧をかけて電流を流すことになる。従って、電源電圧の高電圧の取り扱いに注意する必要がある。また、測定対象以外に流れる漏洩電流(リーク電流)にも対策が必要である。
体積絶縁抵抗の測定
絶縁材料内部を流れる電流に注目し、その流れにくさを表す係数を体積抵抗と呼びます。前節のガードの説明では、測定回路内にガード用の端子・電気的接点を設けていました。体積抵抗の測定では、電極側にガードの為の電気的接点を設けることで、絶縁材料表面を流れる電流を妨げます。
体積抵抗測定の原理的な構成を図8に示す。計測したい電流が流れ出る側を主電極、その反対側を対電極とする。測定対象の内部を通る電流\(I_v\)が電流計に入力され、表面を通る電流(図の青矢印)はガード電極によって遮られる。電圧 \(V\)を印加したときに測定対象の内部を通る電流\(I_v\) は、\(R_v = \frac{V}{I_v}\)の関係で表される。この時の\(R_v\) を体積抵抗と呼ぶ。ただし、体積抵抗は電極の形状・寸法・電極の間隔に影響される。
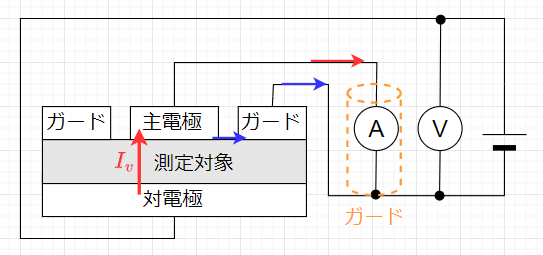
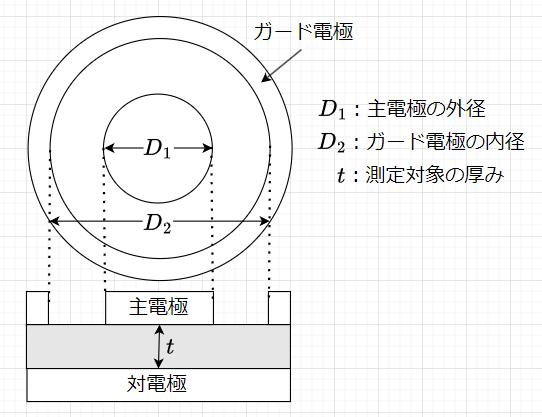
主電極の外径を\(D_1\) 、ガード電極の内径を\(D_2\)とすれば、この2つの電極間の隙間が主電極の半径より十分狭い場合、体積抵抗率は、$$\rho_v = R_v \frac{ \pi D_1^2}{4 t}$$となる。ここで、 \(\left(\frac {D_2 - D_1}{2} \ll \frac{D_1}{2}\right)\)のとき、電流密度が一様な主電極の面積は\(S = \pi \left(\frac{D_1}{2}\right)^2\)とする。
しかし、実際に使用する場合は、「主電極とガード電極間の距離」と「主電極の半径」が理想的な設定にはならないので、補正が必要である。
※詳細は、「絶縁抵抗測定の手引き(日置電機㈱)」を参照願います。
絶縁抵抗の測定
絶縁抵抗の値を計測するものが絶縁抵抗計で、「メガー(メガテスター)」と呼ばれる事も多い。測定原理としては、測定物へ抵抗計内部の電源で直流高電圧を発生させ、測定対象にその電圧を印加し、絶縁抵抗に流れる微小な電流を測定して抵抗値を導きだす。
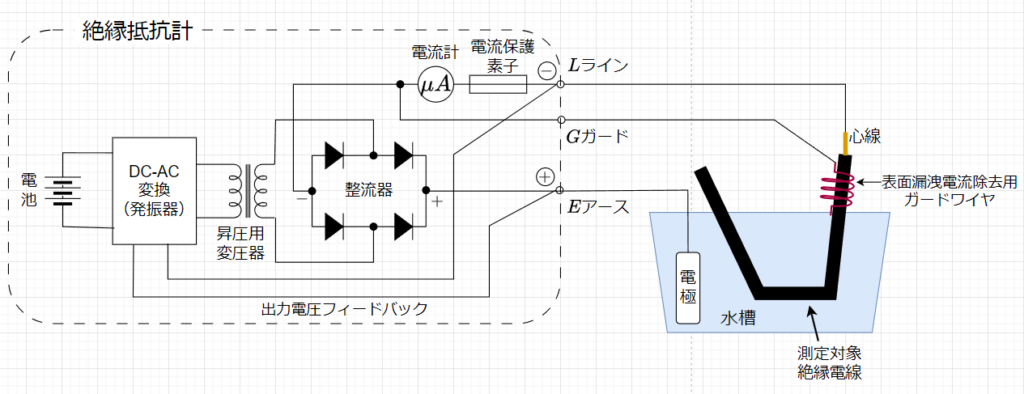
図10に電池式絶縁抵抗計を示す。絶縁抵抗計の基本構造は、直流電流源と電流計、電流保護素子から成る。LINE端子(L端子)とEARTH端子(E端子)との間に測定対象を接続する。E端子は、直流電源の+(正極)に、L端子はー(負極)に接続するため、測定電流はE端子から測定対象を通り、L端子へ流れる。測定の際には、アース測定コードを接地端子(大地)側に接続する。これは、大地に対する絶縁測定や測定対象の一端が接地されているときには、大地側に+極を接続する方が抵抗値が小さく出る(すなわち、絶縁測定としては厳しい方向の試験となる)のが普通であり、絶縁不良の検知には最適であるとされている。
※メガテスターの実践的な使い方は、「メガテスターの使い方とモーターの絶縁測定」「絶縁抵抗の測定方法」を参照願います。
接地抵抗の測定
接地抵抗とは、土壌に接した電極から大地に流れる電流に対する抵抗である。この土壌の抵抗率は金属に比べると非常に大きいため、金属の接触抵抗とは性質が大きく異なる。金属の接触抵抗の影響範囲は、電極との接触面のみを考えて実用上問題ないが、接地抵抗の場合は影響範囲が接地電極と土壌との接触抵抗のほかに、土壌の大きな抵抗率により、接地電極から離れた箇所まで及ぶ。 従って、接地抵抗は、 「接地電極から大地へ接地電流 \(i \; [A]\)が流れると、接地電極の電位が周辺の大地より\(v\;[V]\)高くなる。この電位上昇と接地電流の比\(v/i\; [\Omega]\)をその接地電極の接地抵抗とする」と定義される。この場合の電位上昇の測定は、接地電極から十分離れた場所との間で測定しなければならない。電極間は10~20 m 程度離すと、電極の影響を受けずに接地抵抗を測定できる。図11に接地電極間の電位の概念図を示す。
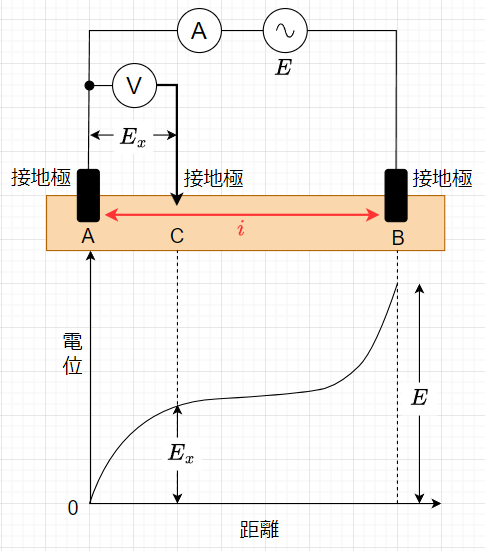
また、電源には交流を使用する。これは、接地電極を埋設する表層付近の土壌は腐食有機物の混入などのため、電解質的な特性を持ち、直流電流を流すと分極作用のため、時間とともに電流が流れ難くなり大きな誤差を生じるためである。なお、使用する交流電源の周波数は電源からの誘導の影響を分離するため、商用周波数以外のものを使用する。但し、高い周波数だとリード線のインダクタンスや静電容量の影響を受けるため、一般的には、\(1\;kHz\)以下が採用される。
接地極A地点の接地抵抗\(R_x\)は、A-B間の抵抗を\(r_a\)、B-C間の抵抗を\(r_b\)、C-A間の抵抗を\(r_c\)、接地極Bの地点の接地抵抗を\(R_B\)、接地極Cの地点の接地抵抗を\(R_C\)とすると、$$r_a = R_x + R_B ,\;\;\;\; r_b = R_B + R_C ,\;\;\;\; r_c = R_C + R_x$$ なので、これらの式から\(R_x\)を求めると、$$R_x = \frac{r_a - r_b + r_c}{2}$$となる。
※接地抵抗測定の詳細に関しては、「接地抵抗測定ガイド(共立電気計測㈱)」を参照願います。