20. 抵抗・インピーダンスの測定(2)
インピーダンスを精度よく測定するために重要な要素は、測定条件の最適化である。インピーダンス測定器(LCRメータやインピーダンスアナライザなど)を使用する際に必要となる基本的な設定条件をまとめる。
(1) 周波数:最も基本的な条件が周波数である。全ての電子部品には周波数特性が有り、周波数によってインピーダンス値は変化する。インピーダンス測定器の測定精度は、周波数やインピーダンス値に応じて変化する。
(2) 信号レベル:測定端子から出力される交流信号を測定対象に印加するが、その信号レベルは、測定対象に応じて適切に設定する。一般的に信号レベルを大きくしたほうが測定値のばらつきは小さくなるが、測定対象に電気的破壊が生じないかを把握しておく必要がある。
(3) 測定スピード:測定値のばらつきと測定時間はトレードオフの関係にある。 測定スピードを遅くすることで測定値のばらつきは小さくなる。適切な測定スピードを精度と測定時間を考慮して決定する。
(4) 測定レンジ :測定レンジは測定器において測定値のばらつきを左右する重要な要素で、測定レンジを測定対象のインピーダンス値に応じて選択する。
(5) DCバイアス:測定対象に印加されるDCバイアスの影響によって、測定値に変化が生じることがある。レベル依存性のあるコンデンサであればDCバイアス電圧によって静電容量値の変化が生じ、インダクタであれば DC バイアス電流によってインダクタンス値の変化が生じるので、適切なバイアスを調整する必要がある。
インピーダンスの測定には、ディジタルLCRメータやインピーダンスアナライザを使用するのが実務的であるが、その基本測定原理を知っておくことは、測定器の正しい使用法を修得するうえで重要である。
※ディジタルLCRメータについては、https://www.texio.co.jp/product/lists/8/31 等を参照願います。
※インピーダンスアナライザについては、https://www.keysight.com/jp/ja/products/lcr-meters-impedance-measurement-products/impedance-analyzers.html 等を参照願います。
交流ブリッジ
交流ブリッジは、直流ブリッジと同様に、零位法でインピーダンスを測定する際に使われる。図1において、平衡状態の場合(検流計\(D\)に電流が流れない。B-D間の電位が等しい。)、平衡条件が成立し、$$\dot{Z}_1 \dot{Z}_x = \dot{Z}_2 \dot{Z}_3$$となる。
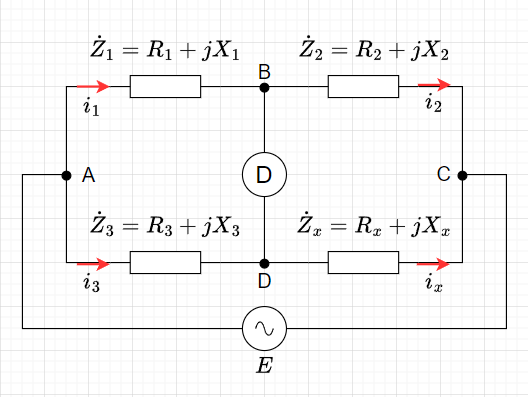
従って、$$(R_1 + j X_1)(R_x + j X_x) = (R_2 + j X_2)(R_3 + j X_3)$$なので、実部と虚部に分けて整理すると、$$(R_1 R_x - X_1 X_x)+ j(R_1 X_x + R_x X_1) = (R_2 R_3 - X_2 X_3) + j(R_2 X_3 + R_3 X_2)$$なので、この等式が成立するのは、$$R_1 R_x - X_1 X_x = R_2 R_3 - X_2 X_3 ,\;\;\;\; R_1 X_x + R_x X_1 = R_2 X_3 + R_3 X_2$$のときなので、この2式を解いて\(R_x,\;X_x\)を求める。$$R_x = \frac{R_1 R_2 R_3 - R_1 X_1 X_3 + R_2 X_1 X_3 + R_3 X_1 X_2}{R_1^2 + X_1^2} \\ X_x = \frac{R_1 R_2 X_3 + R_1 R_3 X_2 - R_2 R_3 X_1 + X_1 X_2 X_3}{R_1^2 + X_1^2}$$以上の式から、測定対象のインダクタンス\(\dot{Z}_x\)を求めるには、\(\dot{Z}_1,\;\dot{Z}_2,\; \dot{Z}_3\)の各抵抗\(R\)と各リアクタンス\(X\)を調整して、平衡状態とする必要がある。これは非常に煩雑になるので、測定対象や用途に応じて、抵抗成分かリアクタンス成分のどちらかを削減するなど、簡略化したブリッジを使用する。
交流ブリッジの標準素子
交流ブリッジは、未知インピーダンスの測定に用いられる回路で、ブリッジの平衡条件を利用して、未知インピーダンスを既知の標準素子の値と比較し測定する。交流ブリッジで使用する標準素子は、以下の基本条件が必要である。
精度が高い、安定性が高い、温度変化の影響を受け難い、周波数変化の影響を受け難い。
標準抵抗器
標準抵抗器に求められる条件として、抵抗率が大きい、抵抗温度係数が小さい、抵抗値が安定している、周波数の影響を受け難い、が重要である。インダクタンス成分やキャパシタンス成分を小さくする工夫をしている。図2に標準抵抗器の外観例を示す。マンガニン線 (銅 84%,ニッケル4%,マンガン 12%の合金) を巻いたもの、または、金属箔抵抗を二重の円筒容器に密封している。 100Ω以下のものでは電流端子と電圧端子とが分れており、電圧端子間が標準抵抗値となっている。
標準インダクタ
標準インダクタは、インピーダンス測定や校正に使用される、高精度で安定したインダクタで、LCRメータなどのインピーダンス測定器の校正、電気回路の設計・デバッグ、
材料の特性評価などに使用される。標準インダクタに求められる条件としては、抵抗がなるべく小さいこと、自己インダクタンスが周波数や電流により変化しないことが求められる。コイルには銅線を使用し、巻枠は経年変化を生じないよう大理石やプラスチックなどを用いる。鉄心は使用しない。

https://www.jemic.go.jp/kousei/capacitor-inductor.html
標準コンデンサ
標準コンデンサとは、静電容量の値を精密に定めたコンデンサで、LCRメータなどのインピーダンス測定器の校正
電気回路の設計・デバッグ、材料の特性評価などに使用される。標準コンデンサに求められる条件は、静電容量が安定で周波数依存性が無いこと、誘電損失が少ないこと、絶縁が良く耐電圧が高いことなどで、無損失空気コンデンサ、可変空気コンデンサが使われる。

TYPE 6250Bシリーズ
https://www.sunjem.co.jp/archives/1625/
インダクタンス\(L\)の測定
インダクタンス\(L\)を測定することができる交流ブリッジを示す。
直列インダクタンスブリッジ
図5に直列インダクタンスブリッジを示す。測定対象は、\(R_x + j \omega L_x\)とする。平衡条件から、$$(R_x + j \omega L_x)R_2 =(R_1 + j \omega L_1)R_3 \\(R_x R_2 - R_1 R_3 ) + j \omega (L_x R_2 - L_1 R_3) = 0$$
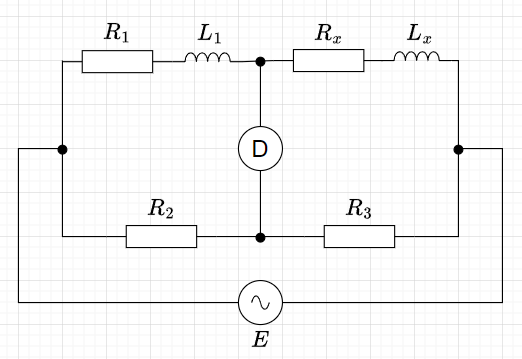
よって、実部=0、虚部=0、つまり、$$R_x R_2 = R_1 R_3 , \;\;\;\;\;\;\;\; L_x R_2 = L_1 R_3$$が成立することが必要である。以上より、$$R_x = \frac{R_3}{R_2} R_1 , \;\;\;\;\;\;\;\; L_x = \frac{R_3}{R_2} L_1$$となり、測定対象の自己インダクタンス\(L_x\)が計測できる。
マクスウェルブリッジ
図6にマクスウェルブリッジを示す。測定対象は、\(R_x + j \omega L_x\)とする。平衡条件から、$$(R_x + j \omega L_x)\left(\frac{R_2 \frac{1}{j \omega C}}{R_2 + \frac{1}{j \omega C}} \right) = R_1 R_3 \\ (R_x + j \omega L_x)R_2 = (1 + j \omega C R_2) R_1 R_3 \\ (R_x R_2 - R_1 R_3) + j \omega (L_x R_2 - C R_1 R_2 R_3) = 0$$
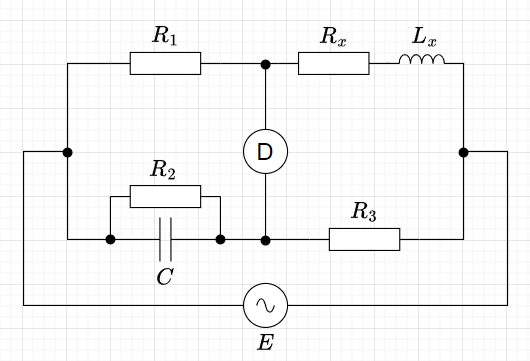
よって、$$R_x R_2 = R_1 R_3 , \;\;\;\;\;\; L_x R_2 = C R_1 R_2 R_3$$が成立することが必要である。以上より、$$R_x = \frac{R_1}{R_2} R_3 , \;\;\;\;\;\;\; L_x = C R_1 R_3$$となり、測定対象の自己インダクタンス\(L_x\)が計測できる。
ヘイブリッジ
図7にヘイブリッジを示す。測定対象は、\(R_x + j \omega L_x\)とする。平衡条件から、$$(R_x + j \omega L_x)\left(R_2 + \frac{1}{j \omega C} \right) = R_1 R_3 $$
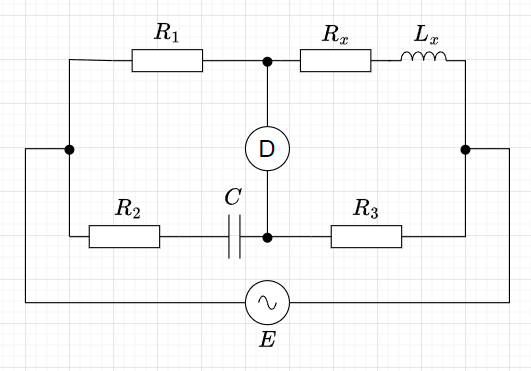
$$\left(R_x R_2 + \frac{L_x}{C} - R_1 R_3 \right) + j \omega \left( L_x R_2 - \frac{R_x}{\omega^2 C}\right) = 0$$よって、$$R_x R_2 C + L_x - R_1 R_3 C = 0 \\ \omega^2 C L_x R_2 - R_x = 0$$この2式より、$$R_x = \frac{\omega^2 C^2 R_1 R_2 R_3}{1 + \omega^2 C^2 R_2^2} , \;\;\;\;\;\;\;\; L_x = \frac{C R_1 R_3}{1 + \omega^2 C^2 R_2^2}$$ となり、測定対象の自己インダクタンス\(L_x\)が計測できる。
ヘビサイドブリッジ(相互インダクタンスの測定)
図8にヘビサイドブリッジを示す。測定対象は、\(R_x + j \omega M_x\)(相互インダクタンス\(M\))とする。また、\(L , \; L_3\)は既知とし、検流計\(D\)に電流が流れないように\(R_1,\;R_2,\;R_3\)を調整して平衡状態にする。図8において、$$I = \dot{I}_1 + \dot{I}_2$$ で、検流計に電流が流れないように調整するので、$$R_1 \dot{I}_1 = R_2 \dot{I}_2 \\ \dot{I_2} = \frac{R_1}{R_2} \dot{I}_1$$となる。
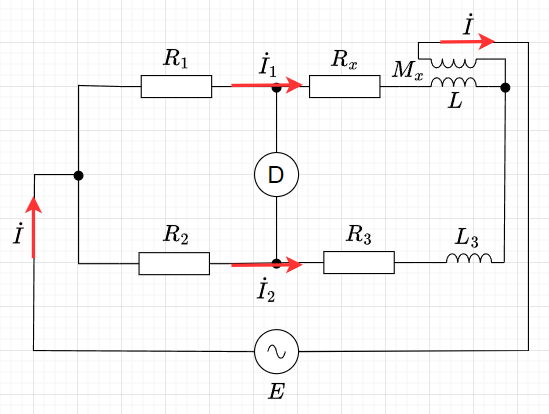
また、\(R_1 \rightarrow R_x \rightarrow L\)の電圧降下と\(R_2 \rightarrow R_3 \rightarrow L_3\)の電圧降下は等しいので、$$(R_1 + R_x + j \omega L) \dot{I}_1 + j \omega M_x \dot{I} = (R_2 + R_3 + j \omega L_3) \dot{I}_2 \\ \left\{R_1 + R_x +j \omega (L + M_x) \right\} \dot{I}_1 = \left\{R_2 + R_3 + j \omega (L_3 - M_x) \right\} \dot{I}_2 \\ \left\{ R_x +j \omega (L + M_x) \right\} \dot{I}_1 = \left\{R_3 + j \omega (L_3 - M_x) \right\} \dot{I}_2 \\ \left\{ R_x +j \omega (L + M_x) \right\} \dot{I}_1 = \left\{R_3 + j \omega (L_3 - M_x) \right\} \frac{R_1}{R_2} \dot{I}_1 $$となる。この式を整理すると、$$(R_x R_2 - R_3 R_1) + j \omega \left\{R_2(L + M_x) - R_1(L_3 -M_x)\right\} = 0$$なので、実部=0、虚部=0、より、$$R_x R_2 - R_3 R_1 = 0 ,\;\;\;\;\;\; R_2 L + R_2 M_x - R_1 L_3 + R_1 M_x = 0$$よって、$$R_x = \frac{R_3 R_1}{R_2} ,\;\;\;\;\;\; M_x = \frac{R_1 L_3 - R_2 L}{R_1 + R_2}$$ さらに、\(R_1 = R_2\) となるように調整すると、$$R_x = R_3 , \;\;\;\;\;\;\; M_x = \frac{L_3 - L}{2}$$となる。
キャパシタンス\(C\)の測定
キャパシタンス\(C\)を交流ブリッジで測定する方法を示す。
並列容量ブリッジ
図9に並列容量ブリッジを示す。測定対象は、\(R_x\)と \( C_x\)とする。平衡条件から、$$R_2\left(\frac{R_x \frac{1}{j \omega C_x}}{R_x + \frac{1}{j \omega C_x}}\right) = R_3 \left(\frac{R_1 \frac{1}{j \omega C_1}}{R_1 + \frac{1}{j \omega C_1}}\right) \\ R_2 \left(\frac{R_x}{1 + j \omega C_x R_x} \right) = R_3 \left( \frac{R_1}{ 1 + j \omega C_1 R_1}\right)$$
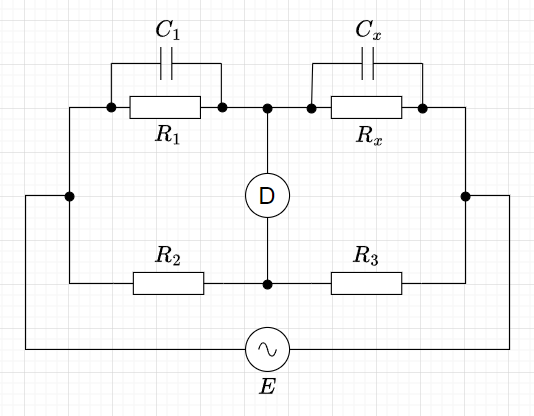
$$R_x R_2 ( 1 + j \omega C_1 R_1) = R_1 R_3 ( 1 + j \omega C_x R_x) \\ (R_x R_2 - R_1 R_3) + j \omega ( R_x R_2 C_1 R_1 - R_1 R_3 C_x R_x) = 0$$ 従って、実部=0、虚部=0、より、$$R_x R_2 - R_1 R_3 = 0,\;\;\;\;\;\; R_x R_2 C_1 R_1 - R_1 R_3 C_x R_x = 0$$ よって、$$R_x = \frac{R_3}{R_2}R_1 , \;\;\;\;\;\;\; C_x = \frac{R_2}{R_3} C_1$$となり、測定対象の抵抗\(R_x\)、キャパシタンス\(C_x\)が計測できる。
シェーリングブリッジ
図10にシェーリングブリッジを示す。測定対象は、\(R_x\)と \( C_x\)とする。平衡条件から、$$R_1 \frac{1}{j \omega C_3} = \left(R_x + \frac{1}{j \omega C_x}\right)\left( \frac{R_2 \frac{1}{j \omega C_2}}{ R_2 + \frac{1}{ j \omega C_2}}\right) $$
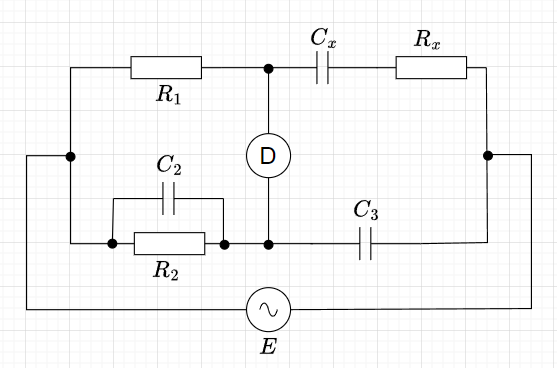
$$ j \omega C_x R_1 (1 + j \omega C_2 R_2) = j \omega C_3 R_2 (1 + j \omega C_x R_x) \\ \omega^2 ( C_x R_x C_3 R_2- C_x R_1 C_2 R_2) + j \omega (C_x R_1 - C_3 R_2) = 0$$従って、実部=0、虚部=0、より、$$C_x R_x C_3 R_2= C_x R_1 C_2 R_2 , \;\;\;\;\;\;\;\; C_x R_1 = C_3 R_2$$ よって、$$R_x = \frac{C_2}{C_3} R_1 ,\;\;\;\;\;\;\; C_x = \frac{R_2}{R_1} C_3$$となり、測定対象の抵抗\(R_x\)、キャパシタンス\(C_x\)が計測できる。
ウィーンブリッジ
図11にウィーンブリッジを示す。測定対象は、\(R_x\)と \( C_x\)とする。平衡条件から、$$\left(R_1 + \frac{1}{j \omega C_1}\right) R_3 = \left(\frac{R_x \frac{1}{ j \omega C_x}}{R_x + \frac{1}{j \omega C_x}}\right) R_2 \\ R_3 ( 1 + j \omega C_1 R_1)( 1 + j \omega C_x R_x) = R_x R_2 j \omega C_1$$
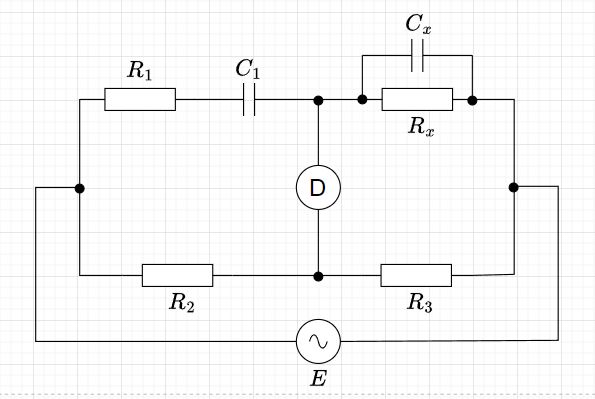
$$R_3 (1 - \omega^2 C_1 R_1 C_x R_x ) + j \omega( C_1 R_1 R_3 + C_x R_x R_3 - R_x R_2 C_1 ) = 0$$従って、実部=0、虚部=0、より、$$ \omega^2 = \frac{1}{C_1 R_1 C_x R_x} , \;\;\;\;\;\;\; \frac{R_1}{R_x} + \frac{C_x}{C_1} = \frac{R_2}{R_3}$$となる。平衡条件に\(\omega\)が含まれていることから、特定の周波数での特性を測定する際に使われる。
\(Q\)メータ
\(Q\)メータは、コイルの\(Q\)値を測定するための測定器である。\(Q\)値はコイルの品質を表す指標で、コイルの損失の小ささを表す。\(Q\)値が高いほど、コイルの損失が少なく、効率的に電磁エネルギーを蓄積・放出することができる。
\(Q\)値
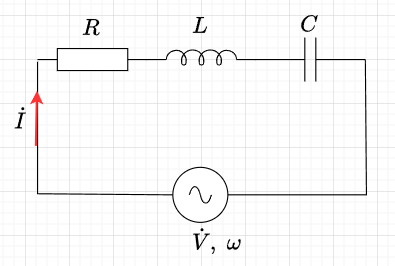
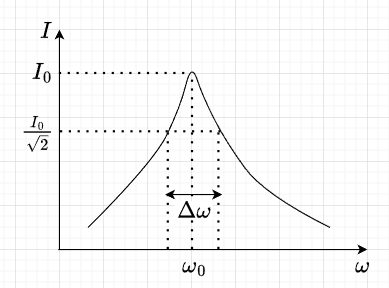
\(Q\)値は共振の鋭さを表す指標である。図12にRLC直列共振回路を示す。図13に示すように、角周波数\(\omega_0 = \frac{1}{\sqrt{LC}}\)のとき電流が最大値\(I_0 \)となる。この状態を共振という。\(\omega_0\)を共振角周波数という。( \(f_0 = \frac{1}{2 \pi \sqrt{LC}}\):共振周波数)
共振角周波数\(\omega_0\)のときの最大電流\(I_0\)の\(\frac{1}{\sqrt{2}}\)となる角周波数の幅を\(\Delta \omega\)とすると、\(Q\)値は、$$Q = \frac{\omega_0}{\Delta \omega} = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 CR}$$と表す。
※RLC直列回路についての詳細は、26. RLC直列回路、30. 直列共振と並列共振を参照願います。
\(Q\)値の測定
\(Q\)メータは、コイルの特性評価、共振回路の調整、フィルタ設計、インピーダンスマッチングなど、無線機器や電子回路の設計・開発に広く用いられる。図14に\(Q\)メータの基本構造を示す。測定対象を\(\dot{Z} = R_x + j \omega L_x\)として、同調コンデンサを調整して電圧計Vの読みが最大になるように共振点を探す。
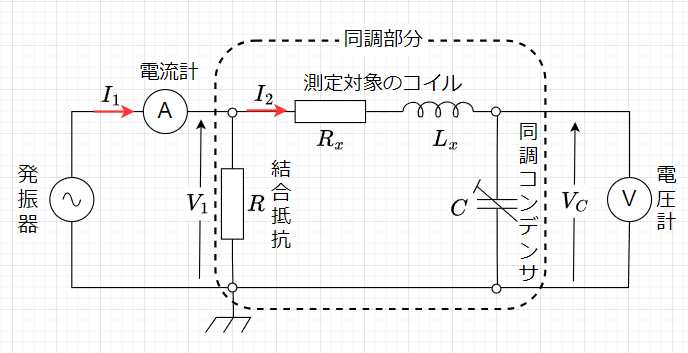
共振状態では、電流計Aの指示値\(I_1\)は、\(R \ll R_x\)であれば、\(I_1\)はほとんど\(R\)に流れるので、\(V_1 \approx I_1 R\)となり、\(I_2 \approx \frac{V_1}{R_x}\)となる。従って、共振状態における電圧計Vの読みを\(V_C\)とすると、$$V_C = \frac{I_2}{\omega C} = \frac{V_1}{R_x} \cdot \frac{1}{\omega C}$$であり、$$Q = \frac{1}{\omega C R_x} = \frac{V_C}{V_1}$$となる。よって、\(V_1\)を一定値にすることで、\(V_C\)から\(Q\)値が直読できる。
また、共振状態のとき、\(\omega_0^2 C L_x = 1\)なので、$$L_x = \frac{1}{\omega_0^2} , \;\;\;\;\;\;\;\;\; \omega_0 = 2 \pi f_0$$となる。従って、共振状態での\(Q\)メータの発振周波数\(f_0\)と同調コンデンサ\(C\)の値から\(L_x\)が算出できる。


