2. 電界と電界の強さ
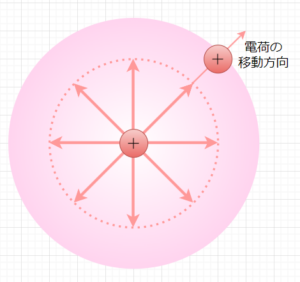
電界(電場)とは、電荷に力を及ぼす空間の性質の一つである。電荷の周りには電界が存在し、電荷に力を与える。電界は、ベクトル量であり、大きさと方向を持つ。電界の大きさは、その点における単位電荷が受ける力と、その電荷の電気量の比で表す。電界の方向は、電荷に働く力の向きと同じである。電界の単位は、国際単位系(SI)では\([N/C]\)で、\(1\;C\)の電荷が\(1 \;N\)の力を受けるのが電界の強さである。電界は目に見ることはできないが、電荷の動きによってその存在を知ることができる。例えば、帯電した棒を静電気放電検知器に近づけると静電気放電検知器の針が動くのは、電界によって静電気放電検知器に力が働いているからである。
電界の強さ
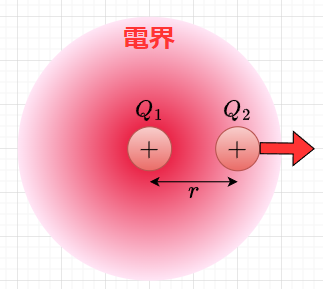
電荷の周囲には静電力の働く場(電界、電場)が存在する。図1のように、空間の一点に電荷\(Q_1\)があり、これより\(r\;[m]\)離れたところに電荷\(Q_2\)があるとすると、\(Q_1,\;Q_2\)の間にはクーロン力が働く。この場合、電荷\(Q_1\)により静電力の及ぶ場(電界)が形成されており、その場に電荷\(Q_2\)が置かれることでクーロン力が働くと考えることができる。この電荷\(Q_2\)の場所(電荷\(Q_1\)から\(r\;[m]\)離れた場所)における電界\(E\)は、クーロンの法則を使って、真空中では、$$F =\frac{Q_1 Q_2}{4 \pi \epsilon_0 r^2} \;[N]\;\;\;\;E=\frac{F}{Q_2} \;[N/C]\;\; \cdots \cdots(1) \\ F=Q_2 E \;[N]$$と表すことができる。電界は、真空中、空気中、各種媒体内に存在する3次元の場(ベクトル場)として扱う。電荷の周りに生じる電界の強さは、その電荷の大きさ、電荷からの距離、電界の存在する場の物質の種類によって異なる。電界の大きさとその方向を定量的に表すときに電界の強さを用いる。式(1)より、電界の強さは、「単位正電荷(\(+1 \;C\))当たりの静電力」といえる。また、電界の方向は、「正電荷を置いたときに働く静電力の方向」で表される。
電界の強さの単位
電界の強さの単位は、$$E = \frac{F}{Q} $$より、\([N/C]\)である。
ここで、\([N]=[J/m]\)であり、\([J] =[W \cdot s] = [A \cdot V \cdot s]\)、また、\([C] = [A \cdot s]\)なので、$$\left[ \frac{N}{C}\right] = \left[ \frac{A \cdot V \cdot s }{m \cdot A \cdot s}\right] = \left[ \frac{V}{m}\right]$$となる。 電気工学系では、電界の強さの単位として、\([V/m]\)を用いることが多い。
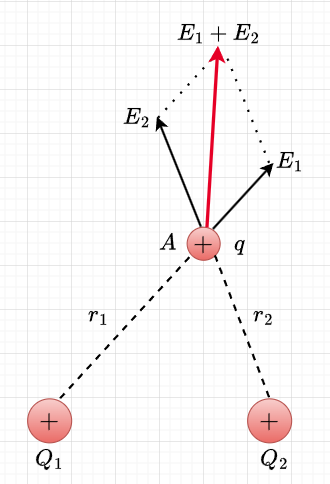
2つの点電荷\(Q_1,\;Q_2\)から\(r_1,\;r_2\)離れた点Aにおける電界の強さ
図2に示すように、\(A\)点に\(q \;[C]\)の点電荷を置いたとき、点電荷\(q\)には、\(Q_1\)によるクーロン力と\(Q_2\)によるクーロン力が働くので、この2つの力のベクトルの和の方向に力が作用することになる。$$F_1 = \frac{Q_1 q}{4 \pi \epsilon_0 r_1^2} ,\;\;F_2 = \frac{Q_2 q}{4 \pi \epsilon_0 r_2^2}$$従って、\(Q_1\)による電界の強さ\(E_1\)、\(Q_2\)による電界の強さ\(E_2\)は、$$E_1 = \frac{F_1}{q} = \frac{Q_1}{4 \pi \epsilon_0 r_1^2} \; [V/m]\\ E_2 = \frac{F_2}{q} = \frac{Q_2 }{4 \pi \epsilon_0 r_2^2}\; [V/m]$$となる。\(Q_1,\;Q_2\)の2つの電荷がつくる\(A\)点の電界の強さ\(\boldsymbol{E}\)は、それぞれがつくる電界のベクトル和となる。$$\boldsymbol{E} =\boldsymbol{E}_1 + \boldsymbol{E}_2$$このように、複数の点電荷によるある一点の電界の強さは、それぞれの点電荷による電界の強さのベクトル和となる。