5. 電流、導体、誘電体
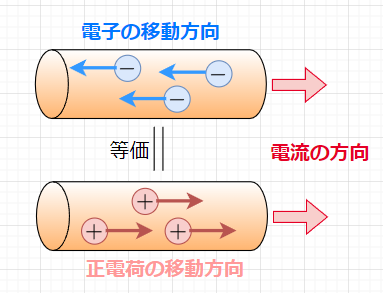
電流とは、電気が導体などの経路を通って流れる様子を指す。具体的には、電荷を帯びた粒子が連続的に動く現象である。電流の大きさは、1秒間にどれだけの電荷が移動するかで決まる。電流の単位は\([A]\)で、\(1\;[s]\)間に\(1\;[C]\)の電荷が移動する電流を\(1\;[A]\)と定義する。また、電流の向きは、電荷が移動する方向によって決まる。一般的には、電子が移動する方向と反対方向を電流の方向とする。これは、歴史的な経緯によるもので、電子の存在がまだ知られていなかった頃、正の電荷が移動する方向を電流の方向と定めたからである。(なお、電子の移動方向を電流の方向と定義する場合もある。)電流の強さは、電圧と抵抗によって決まる。電圧は、電流を流そうとする力であり、\([V]\)という単位で表される。一方、抵抗は、電流の流れを妨げる力であり、\([\Omega]\)という単位で表される。オームの法則によると、電流(\(I\))は、電圧(\(V\))と抵抗(\(R\))の比に等しいとされる(\(I = V/R\))。つまり、電圧が高いほど、または抵抗が小さいほど、電流は大きくなる。
電流の大きさ、方向
正電荷を与えた金属と負電荷を与えた金属を金属線で接続すると、金属内に存在する両電荷間の吸引力により、動きやすい負の電荷をもつ自由電子が金属線を通って移動する。この電子の流れが電流である。電流の大きさは、図2に示すように導体のある断面を単位時間当たりに通過する電荷量で定義する。いま電荷\(Q \;[C]\)がある断面を\(t\;[s]\)間に一様な割合で移動するとき、その断面を流れる電流\(I\)は、$$I = \frac{Q}{t} \;[C/s]\;\; \left([A]\right)$$で表せる。単位は実用的には、\([C/s]\)の代わりに\([A]\)を用いる。電流は、実際には導体中の電子(自由電子)の移動であるから、電子の電荷を\(e\;[C]\)、移動する電子の数を\(1\;[m^2]\)当たり\(n\)個、その電子の速度を\(v\;[m/s]\)とすると、単位時間に移動する電荷、すなわち単位面積を通る電流の大きさは、$$I = nev\;[A]$$である。なお、ある断面を通過する電荷が、時間とともに変化する場合は、微小時間\(\Delta t\)に移動する電荷\(\Delta Q\)を考えれば良いので、$$i = \frac{\Delta Q}{\Delta t} = \frac{dq}{dt} \;[A]$$である。
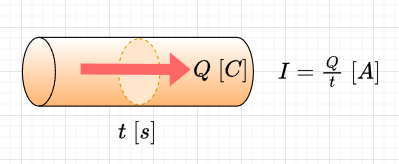
導体、電気抵抗
\(Cu\)銅、\(Au\)金などの金属内部には自由電子(電荷)が無数に存在し、この電荷に外部から静電力などを働かせると自由に移動できる。このように電荷が移動し易い、すなわち電流が流れ易い物質を導体という。ゴムやガラスのように電荷が移動し難い、つまり電流を流さない物質を絶縁体(不導体)という。勿論、導体でも電流に対して抵抗があり、物質により異なる。また、絶縁体でも僅かな電流を流す。導体と絶縁体の中間の性質を持つ物質を半導体という。
※半導体については、1. 半導体の性質 を参照願います。
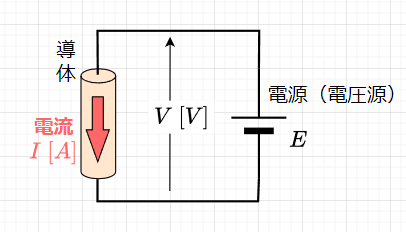

図3に示すように、導体の両端に電圧(電位差)を与えると導体内に電界を生じ、この電界の強さに応じた静電力により電子の流れが生じる。導体に電圧\(V\)を加えるということは電界を与えることであるから、自由電子に静電力が作用することによって電流となる。このとき電流\(I\)は加えた電圧\(V\)に比例する。これは、オームの法則として知られ、$$I = \frac{1}{R} \cdot V$$である。\(R\)は電流の流れ難さ、すなわち電流に対する抵抗を意味する。この\(R\)は電流の流れ難さを表すもので、電気抵抗(抵抗)という。\(R\)の単位は\([\Omega]\)オームである。また、電流の流れやすさを表すのに\(g = \frac{1}{R} \;[S]\)を用いる。\(g\)をコンダクタンスといい、単位は\([S]\)ジーメンスである。
図4に示すような形状の導体の抵抗値は、電流の流れる断面積\(S\)が大きいほど抵抗が小さく、電流の流れる長さ\(l\)が長いほど抵抗が大きい。なお、同じ形状の導体でも導体の種類によって抵抗値が異なる。抵抗値\(R\)は、$$R = \rho \frac{l}{S} \;[\Omega]$$となる。\(\rho\)は抵抗率で、単位は\([\Omega \cdot m]\)である。抵抗率\(\rho\)は、導体(物質)の種類による固有な値である。また、抵抗率の逆数を導電率\(\sigma\)といい、\(\sigma\)の単位は\([S/m]\)である。
※物質毎の抵抗率の例はこちらを参考にしてください。
電界中の導体
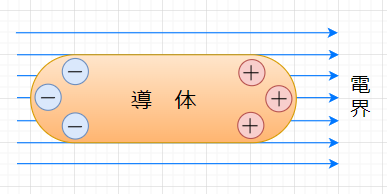
金属の内部には正、負同量の電荷があるため、通常状態では、電気的に平衡で外部に電気的な性質を示さない。図5のように導体に外部から電界を掛けると、導体内部の電荷は静電力を受けて移動し、導体は電気的な平衡がくずれ電荷は導体の両端に分極する。
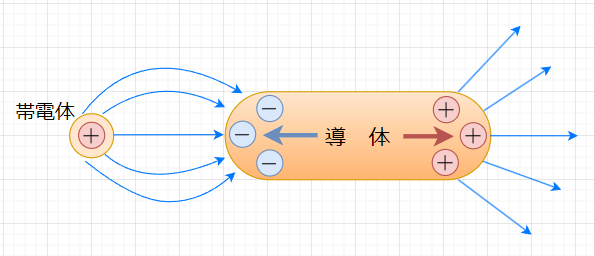
図6のように導体に帯電体(正電荷)を近づけると、導体内部の自由電子(負電荷)が静電力により、帯電体に近い導体の端に吸引され集まる。この結果、他端は正電荷が支配的になる。このように、導体に帯電体を近づけたり、導体を電界中に置いたとき、電子の移動により正、負の電荷が分離して現れる(分極)。この現象を静電誘導という。静電誘導で生じた電荷は、導体内部にあった正、負の電荷が分極したものなので、帯電体を遠ざけたり、電界を取り除くと、正、負の電荷は引き付け合い、中和して電気的に中性の導体に戻る。
電界中の誘電体(絶縁体)
誘電体(絶縁体)の物質を構成する原子は、電子と原子核の結合が強いため、誘電体中の自由電子は極めて少ない。つまり、電流が流れ難い。従って、導体のような静電誘導は起きない。しかし、電界中に誘電体を置いた場合、誘電体の原子に電界による静電力が働くため、原子に電気的な偏りができ、電気双極子(大きさが等しい正負が近接した点電荷)となる。図7のように導体の間に誘電体を挟み、外部から電界をかけると、誘電体の各原子は、図のように電気双極子となるが、誘電体の両端以外の内部では全ての正、負の電荷は互いに打ち消し、誘電体の両端のみに電荷が現れる。この電荷を誘電体の分極電荷という。なお、分極電荷は導体の静電誘導で現れる電荷(真電荷)と異なり、原子から外部に出ることはできない束縛電荷である。
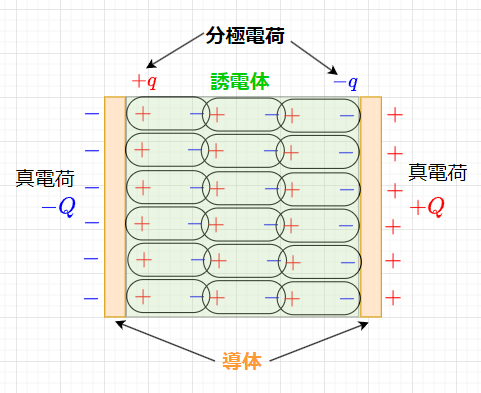
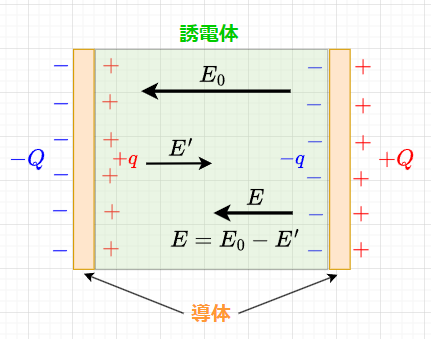
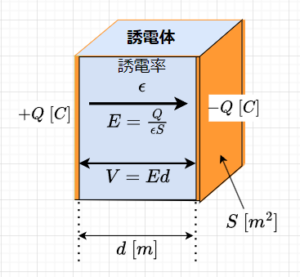
図8で誘電体の分極による電界の強さの変化を考える。図のように平行に配置した導体板に\(+Q\;[C]\)と\(-Q\;[C]\)を電荷を与える。誘電体が無い時(導体板間は真空)の電界の強さを\(E_0\)とする。導体板の面積を\(S \;[m^2]\)とすると、$$E_0 = \frac{Q}{\epsilon_0 S} \;[V/m] $$である。この平行導体板間の電界中に誘電体を入れる。この時、図8のように分極電荷\(+q\;[C]\)と\(-q\;[C]\)が現れる。この分極電荷は、導体板の電荷(真電荷)とは正、負が反対となる。この分極電荷\(+q \;,\;-q\)によって、\(E_0\)と逆向きの電界の強さ\(E'\)が生じる。その結果、誘電体中の電界の強さ\(E\)は、$$E = E_0 - E' \;[V/m]$$となる。$$E' = \frac{q}{\epsilon_0 S} \;[V/m]$$とすると、$$E = \frac{Q - q}{\epsilon_0 S} = \frac{Q}{\epsilon_0 S}\left(1 - \frac{q}{Q} \right) \;[V/m]$$となる。従って、一定の外部電界に対して分極電荷\(q\)が大きくなる誘電体ほど、その内部の電界の強さは弱められることになる。
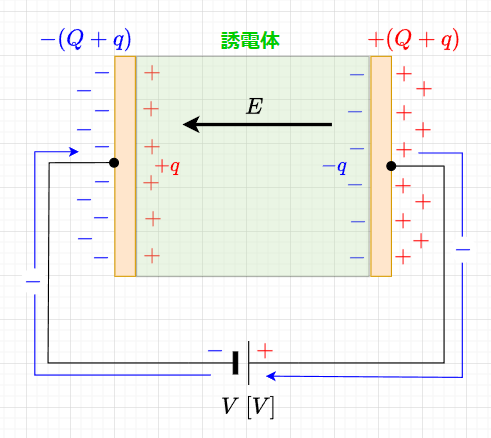
つぎに、図9のように外部から一定の電位差\(V \;[V]\)を加えたときを考える。誘電体が無い場合と誘電体が有る場合とも、外部から加えた電圧は一定であるので、両方とも電界の強さは変化がなく、\(E_0 = E\)である(\(E_0\)は誘電体が無い場合の電界の強さ)。しかし、誘電体の両端には分極電荷\(q\)が発生するので、\(E_0 =E\)の関係を保つためには、分極電荷\(+q\)を相殺するだけの真電荷\(-q\)(自由電子)が、導体板(電極)に電源から余分に送り込まれることになる。つまり、誘電体は絶縁体として電荷の移動を妨げるだけでなく、誘電体中の電界の強さを弱める働きと電極に電荷を誘導する働きがある。つまり、誘電体を電極間に挟むことで、電荷を電源から電極に送り込む働きがある。
誘電率
真空の誘電率\(\epsilon_0\)、一般の物質の誘電率\(\epsilon\)、比誘電率\(\epsilon_s\)とする。誘電体の誘電率を\(\epsilon = \epsilon_0 \epsilon_s\)とすると、図8を参考に、誘電体中の電界の強さ\(E\)は、$$E = \frac{Q}{\epsilon S} = \frac{Q}{\epsilon_0 \epsilon_s S} = \frac{E_0}{\epsilon_s} \;[V/m]$$ である。ここで、誘電体が無い場合の導体板間の電界の強さ\(E_0\)は、$$E_0 = \frac{Q}{\epsilon_0 S}$$である。$$E = \frac{Q}{\epsilon S} = \frac{Q - q}{\epsilon_0 S}$$なので、$$\frac{1}{\epsilon_s} = 1 - \frac{q}{Q} $$よって、$$\epsilon_s = \frac{1}{1 - \frac{q}{Q}}$$である。真空中では、分極電荷は無いので、\(q = 0\)として、\(\epsilon_s =1\)である。分極電荷\(q\)が外部電極の真電荷\(Q\)の大きさに近いほど比誘電率\(\epsilon_s\)は大きくなる。つまり、比誘電率\(\epsilon_s\)は、電界の強さをどの程度弱めるかを表す誘電体の種類によって決まる定数である。空気の比誘電率は\(\epsilon_s \simeq 1\)として扱われる。また、誘電率の大きい物質(例えば、セラミックコンデンサの材料であるチタン酸バリウム)では、\(\epsilon_s =3000\)にもなる。