6. キャパシタ(コンデンサ)
静電容量は、電子部品のキャパシタ(コンデンサ)が蓄えられる電荷の量を表す指標で、単位はファラッド\([F]\) である。\(1\;F\) は \(1\:C\)の電荷を\(1\;V\) の電圧で蓄えることができることを意味している。キャパシタの基本構造は、2枚の導体板 (電極) とその間に挟まれた誘電体(絶縁体)で構成される。これに電圧を印加すると、電極に電荷が蓄えられて電場が発生する。キャパシタは、様々な電子回路で使用される。キャパシタの用途は、エネルギー貯蔵、ノイズ除去、フィルタリング、カップリング、タイミング調整、などである。キャパシタには、挟まれる誘電体により様々な種類がある。代表的なものとして、セラミックコンデンサ、電解コンデンサ、フィルムコンデンサ、タンタルコンデンサ、がある。
静電容量
図1のように、2つの導体板の一方に\(+Q\;[C]\)、他方には\(-Q\;[C]\)の電荷を与えたとすると、2導体板間には電圧\(V\;[V]\)が生じる。逆に、2導体板間に\(V\;[V]\)の電圧を与えると、同じ\(+Q.\;-Q\)の電荷を持つ。このとき、2導体板間の電圧\(V\;[V]\)と2導体板間に蓄積する電荷\(Q\;[C]\)とは比例する。この比例定数を\(C\)とすると、$$Q = C V \;\;[C]$$であり、$$C=\frac{Q}{V}\;\;[C/V]$$である。
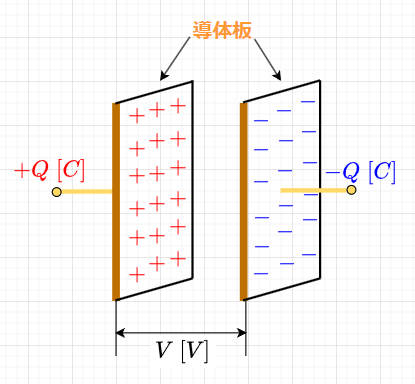
この\(C\)を静電容量という。なお、2導体板間に蓄積される電荷が\(Q\;[C]\)ということは、2導体板の一方に\(+Q \;[C]\)、他方に\(-Q\;[C]\)蓄積されるということを意味している。
静電容量\(C\)の単位は、\([C/V]\)であるが、実用的には、\([F]\)(ファラッド)を使用する。
静電容量の値
静電容量の大きさ\(C\)を求めるには、1つの導体に電荷\(Q \;[C]\)を与えたとして、このときの電位\(V\;[V]\)を計算により求め、この\(Q\;[C]\)と\(V\;[V]\)から\(1\;V\)あたりの電荷\(Q\;[C]\)を計算すればよい。または、\(V\;[V]\)を与えたときの\(Q\;[C]\)を求め、\(1\;V\)あたりの電荷\(Q\;[C]\)を計算することで\(C\)を求めることができる。静電容量の大きさは、\(V\)と\(Q\)との比で定まる定数なので、加えた電圧や電荷には無関係で、導体の大きさ、形状、2導体間の位置関係、誘電率で定まる。
2枚の平行な導体板間の静電容量
キャパシタの基本的な構造である2枚の平行導体板での静電容量を考える。図2のように、面積が\(S\;[m^2]\)の2枚の導体板を間隔\(d\;[m]\)で平行に配置し、この導体板間に誘電率\(\epsilon\)の誘電体を挟む。2枚の導体板にそれぞれ\(+Q\;[C]\)と\(-Q\;[C]\)の電荷を与えたとすると、導体板間の電界の強さは、$$D = \epsilon E ,\;\;\;D = \frac{Q}{S}$$なので、$$E =\frac{Q}{\epsilon S} \;[V/m]$$となる。
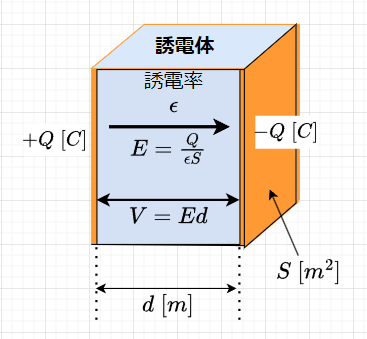
また、導体板間の電位差\(V\)は、$$V = Ed = \frac{Qd}{\epsilon S} \;[V]$$となる。よって、静電容量\(C\)は、$$C = \frac{Q}{V} = \frac{Q}{Qd/\epsilon S} = \frac{\epsilon S}{d} = \frac{\epsilon_0 \epsilon_s S}{d} \;[F]$$となる。これより、平行平板間の静電容量は、電極面積と比誘電率が大きいほど、また、電極板間の間隔が小さいほど大きくなることがわかる。
同軸円筒導体間の静電容量
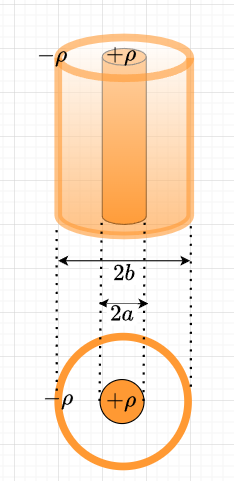
図3に示すような同軸円筒導体間の静電容量を考える。内部導体の直径を\(2a \;[m]\)、外部円筒導体の内径を\(2b \;[m]\)とし、同軸円筒は十分に長いとし、単位長さ当たりの静電容量を求める。同軸円筒の単位長さ当たり、内部導体には\(+ \rho \;[C]\)、外部導体には\(- \rho \;[C]\)の電荷を与えたとする。2導体間の電気力線は、内部導体から外部円筒導体に向かって放射線状に一様に分布していると考えられるから、円筒内部の任意の半径\(x\;[m]\)における電界の強さ\(E\)は、$$E = \frac{\rho}{2 \pi \epsilon_0 x} \;[V/m]$$となる。従って、2導体間の電位差\(V\)は、$$V = - \int_{x=b}^{x=a} E dx \;[V] \\ V = \frac{\rho}{2 \pi \epsilon_0} \cdot \ln\frac{b}{a} \;[V]$$となる。以上より、静電容量\(C\)は、$$C = \frac{\rho}{V} = \frac{\rho}{\frac{\rho}{2 \pi \epsilon_0} \ln \frac{b}{a}} = \frac{2 \pi \epsilon_0}{\ln \frac{b}{a}} \;[F/m]$$となる。
円筒導体に電荷が一様分布するときの電界
半径\(a \;[m]\)の無限円筒導体に単位長さ当たり\(\rho \;[C/m]\)の電荷が一様に分布しているとする。円筒導体の中心から\(x \;[m] \;(x >a)\)で長さ\(l \;[m]\)の電気力線が通る円筒状の閉曲面の面積\(S\)は、\(S = 2 \pi x \cdot l \;[m^2]\)であり、この閉曲面内の電荷の総量は、\(Q = \rho l\;[C]\)である。従って、ガウスの定理より、$$\frac{\rho l}{\epsilon_0} = E \cdot 2 \pi x \cdot l$$なので、$$E = \frac{\rho}{2 \pi \epsilon_0 x} \;[V/m]$$
※キャパシタ(コンデンサ)の接続と合成容量に関しては、11. コンデンサの構造と性質 を参照願います。
※キャパシタ(コンデンサ)と抵抗による過渡特性、周波数特性に関しては、39. 過渡現象 、 14-1. バタワースフィルタ などを参照願います。