8. 電流と磁界
電流と磁界には密接な関係がある。導線などに電流が流れると磁界が発生し、逆に磁界変化によって起電力が発生し、電流が流れる。この関係を理解することは、電気工学などの応用分野で非常に重要である。
・電流による磁界:導線に電流が流れると、その周囲に磁界が発生する。磁界の向きは、右ねじの法則に従う。右手を導線に巻きつけ、親指の方向を電流の方向にすると、残りの指の方向が磁界の方向となる。磁界の強さは、電流が大きいほど、導線からの距離が近いほど強くなる。
・磁界による電流(電磁誘導):磁界が変化すると、その変化に垂直な方向に起電力が発生する。この現象を電磁誘導と呼ぶ。誘導起電力の大きさは、磁界変化が速いほど大きくなり、導線に流れる電流(誘導電流)が大きくなる。
電流がつくる磁界
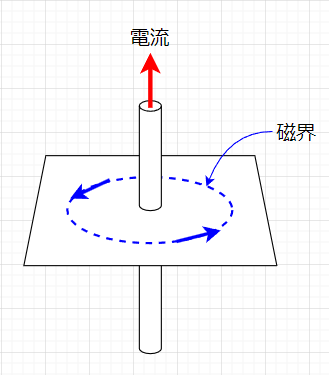
図1「電流による磁界」において、右手の親指を電流の方向(赤矢印)にとると、残りの指の方向が磁界の方向(青点線、青矢印)となる。このように、電流が流れる周辺には必ず磁界が発生する。逆に言うと、磁気が存在するところには、何らかの電流が存在していることになる。「電流は磁界の根源」といえる。直線電流の周りの磁界の方向は、電流に直角な方向となるので、電流に直角な面を想定すると、この面上に電流を中心とした同心円状の磁力線が存在することになる。
コイルに流れる電流のつくる磁界
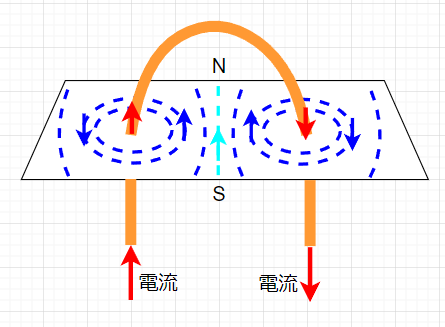
電流のつくる磁界は、電流の流れる形状がどんな形であっても、局所的に見れば電流に対して常に直角になる。ところが、図2のように電流が曲線状に流れた場合の磁界は、電流の各局所ごとに形成される磁界の合成となる。図2のように円形コイルの中心部の磁界は、水色矢印で示すように手前が「S」、奥側が「N」となる(磁針を円形コイルの中心に置くと、N極が矢印の方向に向くということ)。これは、右手で電流の流れる方向に親指以外を巻きつけるようにしたとき、親指の方向が「N」になることを示している。
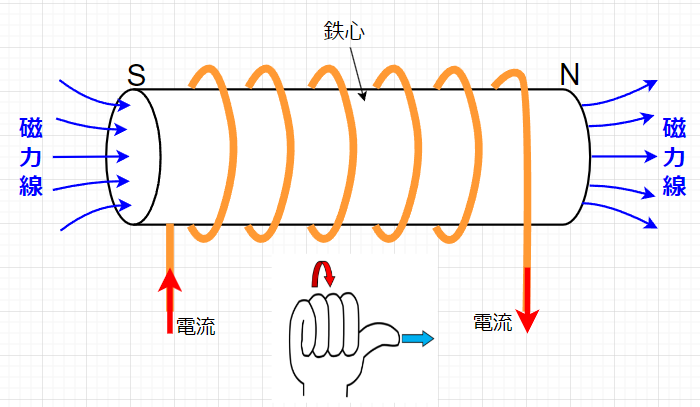
さらに、図3のように電線を筒形に巻いたコイル(ソレノイド)に電流を流した場合の磁界は、図2のようにコイルの局所毎で考えた磁界を合成したものになる。結果的に、電流の流れる方向に親指以外を巻きつけるようにしたとき、図3に示すように親指の方向が「N」極、反対側が「S」極となる。磁力線はコイルの端から端まで貫くような形になる。これは、棒磁石のつくる磁界の状態と同様で、磁力線の出口側が「N」極、入口側が「S」極に相当する。さらにコイルの中に鉄心などの強磁性体を入れることで磁束密度が増加する。この鉄心入りコイルが電磁石である。
アンペアの右ネジの法則
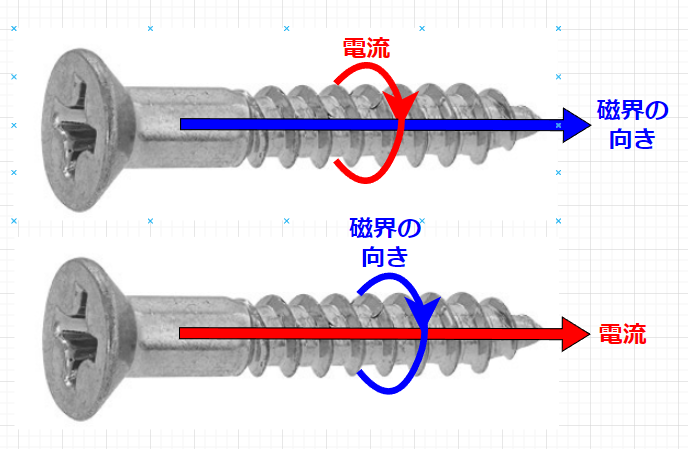
図(上)のように、右ネジの回転方向に電流を流すと、右ネジの進む方向に磁界が生じる。また、図(下)のように、右ネジの進む方向に電流を流すと、右ネジの回転方向に磁界が生じる。このように右ネジにあてはめて、電流と磁界の関係を表す法則をアンペアの右ネジの法則という。
ビオ・サバ―ルの法則
電流の流れる導線の周りにつくられる磁界の方向は、右ネジの法則、磁界の強さに関しては、ビオ・サバ―ルの法則による。この法則により、任意の電流による任意の点の磁界の強さが分かる。図4のように、電線の任意の微小部分\(O\)点に\(I \;[A]\)の電流が流れているとき、\(O\)点から\(r\;[m]\)離れた1点\(P\)における磁界の強さ\(\Delta H\)は、$$\Delta H = \frac{I \Delta l \sin \theta}{4 \pi r^2} \;\;[A/m]$$と表せる。
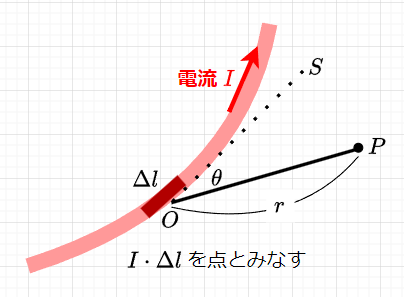
\(\Delta H\)の磁界の方向は、右ネジの法則に従う。ここで、\(\theta\)は、電流が流れる部分\(\Delta l\)の接線\(OS\)と\(OP\)とがなす角である。電流には方向があり、この電流と直角方向の磁界が最大で、電流の方向には磁界が発生しないので、\(\sin \theta\)が関係することになる。また、電流に比例して生じるのは磁界で、磁界には透磁率は関係しない。透磁率によって変化するのは磁束密度なので、ビオ・サバ―ルの法則を磁束密度の式で表すと、$$\Delta B = \mu_0 \Delta H = \frac{\mu_0 I \Delta l \sin \theta}{4 \pi r^2} \;\;[T]$$である。
円形コイルの中心における磁界の強さ
図5のように、半径\(a \; [m]\)の円形コイルに\(I \;[A]\)の電流を流したときのコイルの中心\(O\)点における磁界の方向は、右ネジの法則により、電流の流れる方向から、画面の表から裏の方向であることが分かる。磁界の強さ\(H\)をビオ・サバ―ルの法則から求める。まず、コイル上の微小部分\(\Delta l_1\)をとり、この\(\Delta l_1\)部分の電流による\(O\)点の磁界\(\Delta H_1\)を考える。
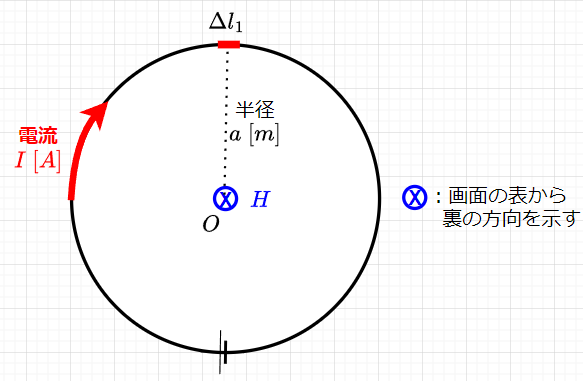
\(\Delta l_1\)部分の電流の向きと半径方向とは\(\theta = \pi /2\)で、距離\(r\)は\(a\;[m]\)なので、\(\sin \theta = 1\) , \(r=a\)であり、$$\Delta H_1 = \frac{I \Delta l_1}{4 \pi a^2}$$となる。この関係は、コイルの円周上のどの点でも成立し、\(O\)点における磁界\(\Delta H_i\)の方向は同じなので、$$H = \Delta H_1 + \Delta H_2 + \Delta H_3 + \cdots = \frac{I}{4 \pi a^2} (\Delta l_1 + \Delta l_2 + \Delta l_3 + \cdots)$$となる。また、\(\Delta l_1 + \Delta l_2 + \Delta l_3 + \cdots = 2 \pi a\) (コイルの円周)なので、$$H = \frac{I}{4 \pi a^2} \times 2 \pi a = \frac{I}{2a} \;\;[A/m]$$となる。さらに、コイルがまとめて\(N\)回巻いてあるとすると、$$H = \frac{I N}{2a} \;\;[A/m]$$となる。
アンペアの法則
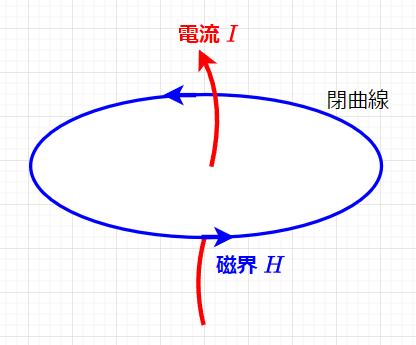
アンペアの法則は、「磁界中に任意の閉曲線を考えた時、その閉曲線に沿ってとった磁界の強さと長さのとの積の和は、その閉曲線内を通る電流の代数和に等しい」というもので、周回積分を導入すると、任意の閉じたループに沿った磁界の周回積分が、そのループを貫く電流の総和に等しいとなる。つまり、$$\oint \mathbf{H} \cdot d\mathbf{l} = I_{\text{enc}}$$ここで、\(\mathbf{H}\)は磁界の強さ、\(d\mathbf{l}\)はループ上の微小な長さのベクトル、\(I_{\text{enc}}\)はループ内を貫く電流の総和とする。


“8. 電流と磁界” に対して1件のコメントがあります。
コメントは受け付けていません。