9-1. 可制御性、可観測性(演習)
離散時間システムの可制御、可観測条件 連続時間システムの状態方程式が、$$\frac{dx}{dt} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} x + […]
8-1. 離散時間システムの安定性(演習)
離散時間システムの安定性の基準 離散時間システムの特性方程式のすべての根(固有値、伝達関数の極)が単位円の内側に存在する場合、そのシステムは安定である。特性方程式の形は次のように表される。$$\phi(z) = a_0 […]
7-1. 離散時間システムの定常特性(演習)
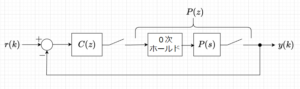
$$P(s) = \frac{1}{s+1}$$の1次系とする。*図1において、0次ホールドを使用して離散化した\(P(s)\)を求める。$$P(z) = (1 - z^{-1})\mathcal{Z} \left\{\ […]
5-1. 離散時間システムの応答(演習)
離散時間システムのインパルス応答 離散時間伝達関数が、$$G(z) = \frac{z + 0.3}{z^2 - 0.7z +0.1}$$のシステムのインパルス応答を求める。 解法1:$$G(z) = \frac{Y(z […]
4-1. 連続時間システムの離散化(演習)
連続時間伝達関数の離散時間伝達関数への変換 (1)\(G(s) = \frac{K}{s}\)を0次ホールドを含む離散化システムに変換する。$$G(z) = (1 - z^{-1})\mathcal{Z}\left\{\ […]
2-1. 留数定理によるZ変換
※以下、虚数単位に「\(j\)」を使用する。 留数定理 留数定理は、特異点の周りで関数を積分する際に、その点における関数の「留数」(Residue:何かが取り除かれた後に残っているもの、という意味)を利用するものである。 […]
1-1. 離散時間制御系の構成(演習)
連続時間システムから離散時間システムへの変換 連続時間システムが微分方程式$$\frac{dy}{dt} = \alpha y + \beta u \;\; \cdots (1)$$で与えられるとき、このシステムをディジ […]