2-1. 留数定理によるZ変換
※以下、虚数単位に「\(j\)」を使用する。
留数定理
留数定理は、特異点の周りで関数を積分する際に、その点における関数の「留数」(Residue:何かが取り除かれた後に残っているもの、という意味)を利用するものである。
ある閉じた経路 \(C\) に沿って解析関数 \(f(z)\) を積分する場合、経路 \(C\) の内部に存在する全ての孤立特異点における留数の和を用いて、積分を簡単に計算できる。
留数定理は次のように表現される。$$\oint_C f(z) \, dz = 2\pi j \sum \text{Res}(f, a_i)$$ここで、
・\(\oint_C f(z) \, dz\) は、閉じた経路 \(C\) に沿った関数\(f(z)\)の複素積分。
・\(\text{Res}(f, a_i)\)は、\(f(z)\)の特異点\(a_i\)における留数。
・\(\sum \text{Res}(f, a_i)\)は、経路\(C\)内の全ての特異点の留数の合計。
留数の定義
関数\(f(z)\)が特異点\(z=a\) で次の形で展開できるとする(ローラン展開)$$f(z) = \frac{c_{-1}}{z-a} + c_0 + c_1(z-a) + \cdots$$ここで、\(c_{-1}\)が特異点\(z=a\)における留数である。
留数定理の証明
1.特異点が1つの場合
関数 \(f(z)\)を \(g(z) = (z-a)f(z)\)と書くと、$$f(z) = \frac{g(z)}{z-a}$$このとき、\(g(z)\) は\(z=a\)で解析的である。よって、$$\oint_C f(z) \, dz = \oint_C \frac{g(z)}{z-a} \, dz$$ここで、Cauchyの積分公式より、$$\oint_C \frac{g(z)}{z-a} \, dz = 2\pi j \, g(a) = 2\pi j \, c_{-1}$$よって、$$\oint_C f(z) \, dz = 2\pi j \, \text{Res}(f, a)$$である。
2.複数の特異点がある場合
複数の特異点がある場合、それぞれの特異点に対して積分を行い、その結果を合計すればよい。$$\oint_C f(z) \, dz = 2\pi j \sum \text{Res}(f, a_i)$$
ローラン展開
ローラン展開は、複素解析における関数の級数展開の一種で、特に特異点を持つ関数の表現に使用される。
複素関数\(f(z)\)がある領域\(A\)で解析的であるとする。\(A\)は、点\(a\)の周りにドーナツ状の領域(孤立特異点\(a\)を含む)である。このとき、関数\(f(z)\)は次の形で展開される。$$f(z)=\sum_{n=-\infty}^{\infty} c_n (z-a)^n$$ここで、\(z=a\)が特異点である場合、\(n \lt 0\)の項が現れることがあり、これがテイラー展開との違いである。
\(c_n\)はローラン係数で、$$c_n = \frac{1}{2\pi j} \oint_C \frac{f(z)}{(z-a)^{n+1}} dz$$ここで、積分経路\(C\)は\(z=a\)を中心とする閉曲線で、関数が解析的な領域に含まれている。
Cauchyの積分公式
\(f(z)\) が\(C\)の内部で解析的で、\(z=a\)に孤立特異点を持つとすると、次の式が成り立つ。$$f(a) = \frac{1}{2\pi j} \oint_C \frac{f(z)}{z-a} \, dz$$
留数定理によるZ変換の求め方
\(f(t)\)をラプラス変換した関数\(F(s)\)の逆ラプラス変換、$$f(t) = \mathcal{L}^{-1} \left[F(s) \right] = \frac{1}{2 \pi j}\int_C F(s) e^{st} ds$$において、サンプル値\(f(kT)\)は\(t = kT\)とおいて、$$f(kT) = \frac{1}{2 \pi j}\int_C F(s)e^{kTs} ds \;\;\;\;\; (k=0,1,2,\cdots) \;\; \cdots(1)$$と表せる。Z変換の定義式$$F(z) = \mathcal{Z} \left[f(kT)\right] = \sum_{k=0}^{\infty} f(kT) z^{-k}$$の右辺に式(1)を代入すると、$$F(z) = \sum_{k=0}^{\infty} \frac{1}{2 \pi j} \int_C F(s) e^{kTs} z^{-k} ds \\ = \frac{1}{2 \pi j} \int_C F(s)\left[ \sum_{k=0}^{\infty} e^{kTs} z^{-k} \right] ds \;\; \cdots (2)$$となる。ここで、$$\sum_{k=0}^{\infty} e^{kTs} z^{-k} = \sum_{k=0}^{\infty} (e^{Ts}z^{-1})^k = \frac{1}{1 - e^{Ts} z^{-1}}$$なので、式(2)は、$$F(z) = \frac{1}{2 \pi j} \int_C \frac{F(s)}{1 - e^{Ts}z^{-1}} ds \;\; \cdots(3)$$と表せる。
\(F(s)\)のすべての極は、閉曲線\(C\)内にあり、かつ、\(C\)内で\(1-e^{Ts}z^{-1} = 0\)となることは無い。よって、式(3)の積分に留数定理を使って、「\(F(z)\)は、\(F(s)\)の極における\(\frac{F(s)}{1 - e^{Ts} z^{-1}}\)の留数の和」となる。
以上より、\(f(t)\)のラプラス変換\(F(s)\)から式(3)により、Z変換を求めることができる。
留数定理を使用したZ変換の例
(1)\(F(s) = \frac{1}{s +a}\)のZ変換を求める。
\(F(s)\)の極は\(s = -a\)であるから、$$F(z) = \left. (s+a)\frac{F(s)}{1-e^{Ts}z^{-1}} \right |_{s=-a} = \frac{1}{1 - e^{-aT} z^{-1}} = \frac{z}{z - e^{-aT}}$$
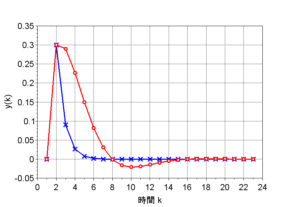
(2)\(F(s) = \frac{1}{s(s+1)(s+2)}\)のZ変換を求める。
\(F(s)\)の極は\(s= 0,\;-1,\;-2\)であるから、求める留数は、
\(s=0\)の留数は、$$\left. s \frac{F(s)}{1-e^{Ts}z^{-1}} \right |_{s=0} = \frac{1}{2(1-z^{-1})}$$ \(s=-1\)の留数は、$$\left. (s+1) \frac{F(s)}{1-e^{Ts}z^{-1}} \right |_{s=-1} = \frac{-1}{1 - e^{-T}z^{-1}}$$ \(s=-2\)の留数は、$$\left. (s+2) \frac{F(s)}{1 - e^{Ts}z^{-1}} \right |_{s=-2} = \frac{1}{2(1 - e^{-2T} z^{-1})}$$となる。従って、$$F(z) = \frac{1}{2(1-z^{-1})} + \frac{-1}{1 - e^{-T}z^{-1}} + \frac{1}{2(1 - e^{-2T} z^{-1})} = \frac{(1 - e^{-T})^2 (1 + e^{-T}z^{-1})z^{-1}}{2(1 - z^{-1})(1 - e^{-T}z^{-1})(1 - e^{-2T}z^{-1})}$$