4-1. 連続時間システムの離散化（演習）

連続時間伝達関数の離散時間伝達関数への変換

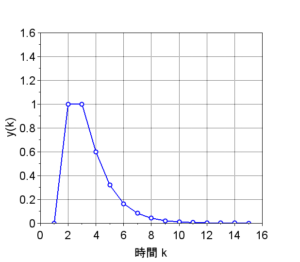
（１）\(G(s) = \frac{K}{s}\)を0次ホールドを含む離散化システムに変換する。$$G(z) = (1 - z^{-1})\mathcal{Z}\left\{\frac{K}{s^2}\right\} \\= (1 - z^{-1}) \frac{KTz}{(z - 1)^2} \\= \frac{KT}{z - 1}$$
（２）\(G(s) =\frac{K}{1 + \tau s}\)を0次ホールドを含む離散化システムに変換する。$$G(z) = ( 1 - z^{-1}) \mathcal{Z} \left\{ \frac{K}{s(1 + \tau s)} \right\} \\=K(1 -z^{-1}) \mathcal{Z} \left\{ \frac{1}{s} - \frac{1}{s + 1/\tau} \right\} \\=\frac{K(z -1)}{z} \left\{ \frac{z}{z-1} - \frac{z}{z - e^{-T/\tau}} \right\} \\=K\cdot \frac{1 - e^{-T/\tau}}{z - e^{-T/\tau}}$$

0次ホールドを含む離散化システム

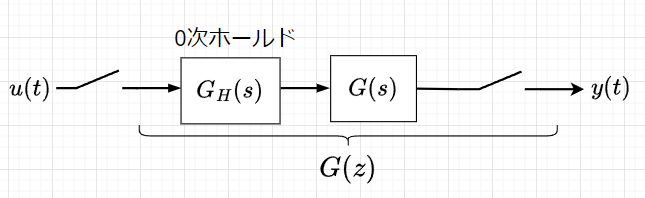
図のように、サンプル値信号がホールド（0次ホールド）されて連続時間システム\(G(s)\)に加えられるようにした離散化システムの伝達関数\(G(z)\)は、$$G(z) = \mathcal{Z}\left\{\frac{1 - e^{-Ts}}{s} G(s) \right\}$$となる。さらに、この式は、$$G(z) = (1 - z^{-1})\mathcal{Z}\left\{\frac{G(s)}{s} \right\}$$と表せる。

連続時間状態方程式から離散時間システムへの変換

連続時間システムの状態方程式を$$\frac{dx}{dt} = \begin{bmatrix} 0 & \omega \\ -\omega & 0 \end{bmatrix} x + \begin{bmatrix} 0 \\ \omega \end{bmatrix} u \\ y = \begin{bmatrix} 1 & 0 \end{bmatrix} x$$としたときの離散化システムを求める。
与えられた状態方程式より、$$F=\begin{bmatrix} 0 & \omega \\ -\omega & 0 \end{bmatrix} , \;\;\; g=\begin{bmatrix} 0 \\ \omega \end{bmatrix}$$とおくと、$$e^{Ft}= \mathcal{L}^{-1} \left[(s I - F)^{-1}\right] = \mathcal{L}^{-1} \left[ \frac{1}{s^2 + \omega^2} \begin{bmatrix} s & \omega \\ -\omega & s \end{bmatrix} \right] = \begin{bmatrix} \cos \omega t & \sin \omega t \\ -\sin \omega t & \cos \omega t \end{bmatrix}$$を使って、$$A = e^{FT} = \begin{bmatrix} \cos \omega T & \sin \omega T \\ -\sin \omega T & \cos \omega T \end{bmatrix} \\ b=\int_0^T e^{F\tau}d \tau \cdot g = \begin{bmatrix} 1 - \cos \omega T \\ \sin \omega T \end{bmatrix} \\ c = \begin{bmatrix} 1 & 0 \end{bmatrix}$$となるので、$$x(k+1) = A x(k) + b u(k) ,\;\;\; y = c x(k)$$である。また、このときのパルス伝達関数は、$$G(z) = c (zI - A)^{-1} b = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} z - \cos \omega T & - \sin \omega T \\ \sin \omega T & z - \cos \omega T \end{bmatrix} ^{-1} \begin{bmatrix} 1 - \cos \omega T \\ \sin \omega T \end{bmatrix} \\= \frac{(1 - \cos \omega T) (z -1)}{z^2 -2z \cos\omega T + 1}$$となる。

Scilabによる解析

\(f= 70\;Hz, \;\; \omega = 2 \pi f, \; T=0.001\)として、インパルス応答を求める。

Scilabスクリプト

clear; clf;
e=%e;
w=2*%pi*70; T=0.001;
F=[0 w ; -w 0];
g=[0 ; w];
c=[1 0];
A = e^(FT);
b=[1-cos(w*T) ; sin(w*T)];
Gz=syslin('d',A,b,c);
Gzz=ss2tf(Gz);
//インパルス応答
u= [1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
y = flts(u,Gzz);
scf(0);plot(y,'-o');

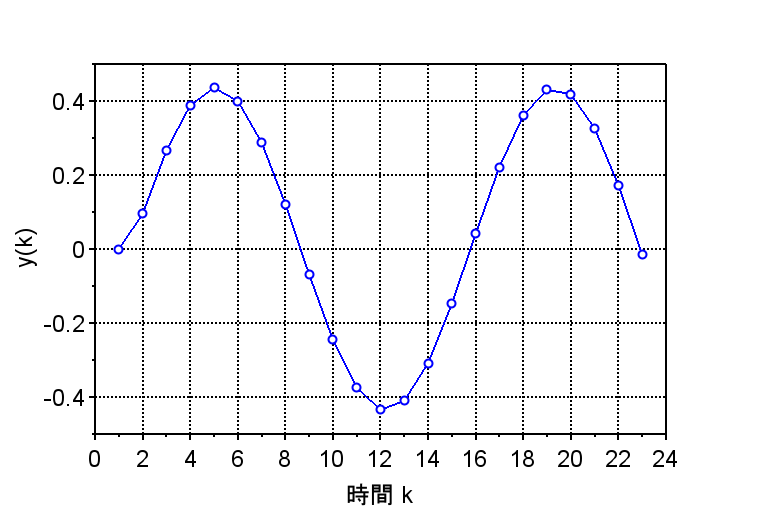
図１のインパルス応答より、このシステムが定常振動することが分かる。また、図より、周波数 約\(70\;Hz\)、周期 \(14 \times 0.001 \;s \)となっていることが読み取れる。