8-1. 離散時間システムの安定性(演習)
離散時間システムの安定性の基準
離散時間システムの特性方程式のすべての根(固有値、伝達関数の極)が単位円の内側に存在する場合、そのシステムは安定である。
特性方程式の形は次のように表される。$$\phi(z) = a_0 z^n + a_1 z^{n-1} + \cdots + a_{n-1} z + a_n=0 \;\;\;(a_0 \gt 0) \;\;\;\; \cdots(1)$$
ここで、\(z\) は複素数で、特性方程式の係数\(a_i\)に基づいてシステムの安定性を判定する。
ジュリーの安定判別法
ジュリーの安定判別法は、離散時間システムの安定性を判定するために用いられる方法で、線形差分方程式や離散時間システムの安定性判定に有効である。この方法は、連続時間システムにおけるラウス・フルビッツの安定判別法に相当する。ジュリーの安定判別法では、まず式(1)を基に以下の表を作成する。
| \(z^0\) | \(z^1\) | \(z^2\) | \(\cdots\) | \(z^{n-1}\) | \(z^n\) |
| \(a_n\) | \(a_{n-1}\) | \(a_{n-2}\) | \(\cdots\) | \(a_1\) | \(a_0\) |
| \(a_0\) | \(a_1\) | \(a_2\) | \(\cdots\) | \(a_{n-1}\) | \(a_n\) |
| \(b_{n-1}\) | \(b_{n-2}\) | \(b_{n-3}\) | \(\cdots\) | \(b_0\) | |
| \(b_0\) | \(b_1\) | \(b_2\) | \(\cdots\) | \(b_{n-1}\) | |
| \(c_{n-2}\) | \(c_{n-3}\) | \(c_{n-4}\) | \(\cdots\) | \(c_0\) | |
| \(c_0\) | \(c_1\) | \(c_2\) | \(\cdots\) | \(c_{n-2}\) | |
| \(\vdots\) | |||||
| \(d_3\) | \(d_2\) | \(d_1\) | \(d_0\) | ||
| \(d_0\) | \(d_1\) | \(d_2\) | \(d_3\) | ||
| \(e_2\) | \(e_1\) | \(e_0\) |
各係数は、$$b_k = \begin{vmatrix} a_k & a_{n-k-1} \\ a_0 & a_{k+1} \end{vmatrix} \;\;\;\;(k=0,1,2,\cdots , n-1) \\ c_k = \begin{vmatrix} b_{n-1} & b_{n-k-2} \\ b_0 & b_{k+1} \end{vmatrix} \;\;\;\;(k=0,1,2,\cdots, n-2) \\ \vdots \\e_k = \begin{vmatrix} d_3 & d_{2-k} \\ d_0 & d_{k+1} \end{vmatrix} \;\;\;\; (k=0,1,2)$$により計算する。
このとき、次の条件が成立するとき、離散時間システムは安定である。
1)\(\left|a_n \right| \lt a_0\)
2)\(\phi(1) \gt 0\)
3)\(\phi(-1) \gt 0 \) (\(n\):偶数)
\(\phi(-1) \lt 0 \) (\(n\):奇数)
4)\(\left| b_{n-1} \right| \gt \left|b_0 \right|\)
\(\left| c_{n-2} \right| \gt \left|c_0 \right|\)
\(\vdots\)
\(\left|e_2 \right| \gt \left|e_0 \right|\)
[例]n=2の場合。$$\phi(z) = z^2 + a_1 z + a_2 = 0$$なので、安定条件は、
1)\(\left| a_2 \right| \lt 1\) すなわち、\(-1 \lt a_2 \lt 1\)
2)\(\phi(1) = 1 + a_1 + a_2 \gt 0\)
3)\(\phi(-1) = 1 - a_1 + a_2 \gt 0\)
となる。
安定な比例ゲインの範囲を求める
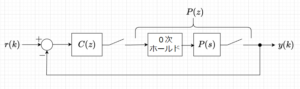
\(G(s) = \frac{K}{s+1}\)を0次ホールドを使った離散時間制御系とし、図1のように閉ループ制御系を構成したとき、制御系が安定となる比例ゲイン\(K\)の範囲を求める。
$$G(z) = (1-z^{-1})\mathcal{Z}\left[\frac{K}{s(s+1)}\right] = \frac{K(1-e^{-T})}{z-e^{-T}}$$である。
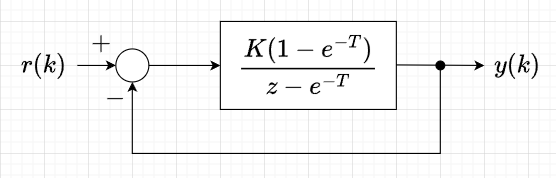
従って、閉ループ伝達関数\(T(z)\)は、$$T(z) = \frac{G(z)}{1+G(z)}$$となる。この特性方程式は、\(1+G(z) =0\)なので、$$ 1 + \frac{K(1-e^{-T})}{z-e^{-T}}=0 \\ z-e^{-T} + K(1 - e^{-T}) = 0$$である。離散時間制御系の安定条件は、特性根(極)が単位円内にあることなので、$$\left| e^{-T} - K(1 - e^{-T}) \right| \lt 1$$これを満たす比例ゲイン\(K\)の範囲は、$$-1 \lt K \lt \frac{1+e^{-T}}{1 - e^{-T}}$$となる。連続時間系の一次系(\(G(s)=\frac{K}{s+1}\))であれば、比例ゲイン\(K\)を大きくしても安定であるが、離散時間系では比例ゲイン\(K\)の大きさに上限があることに注意する必要がある。
安定な状態フィードバックゲインの範囲
離散時間システムの状態方程式を$$x(k+1) = \begin{bmatrix} 0 & 1 \\ -1 & 1 \end{bmatrix} x(k) + \begin{bmatrix} 0 \\ 1 \end{bmatrix} u(k) $$として、状態フィードバック入力\(u(k)\)を$$u(k) = - \begin{bmatrix} f_1 & f_2 \end{bmatrix} x(k)$$とするとき、フィードバック系が安定となるフィードバックゲイン\(f_1 , \;f_2\)を求める。
$$A = \begin{bmatrix} 0 & 1 \\ -1 & 1 \end{bmatrix} ,\;\;\; b = \begin{bmatrix} 0 \\ 1 \end{bmatrix} $$なので、
特性方程式は、$$\phi(z) =\left| zI - (A - bf) \right| \\ = z^2 +(f_2 -1)z + f_1+1=0$$となる。安定条件は、特性根(伝達関数の極)が単位円内にあることなので、ジュリーの安定判別法より、
1)\(\left|f_1 +1 \right| \lt 1\)
2)$$\phi(1) = 1 + f_2 -1 + f_1 +1 \\= f_1 + f_2 +1 \gt 0 \\
f_1 + f_2 \gt -1$$
3)$$\phi(-1) = 1 - (f_2 -1) + f_1 +1 \\= f_1 -f_2 +3 \gt 0 \\f_1 -f_2 \gt -3$$
この3条件を整理すると、
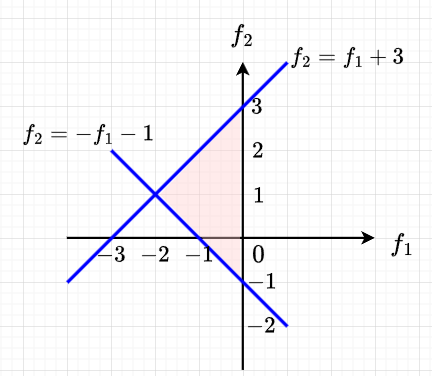
$$ -2 \lt f_1 \lt 0 , \;\;\; f_2 \gt - f_1 -1, \;\;\; f_2 \lt f_1 +3$$ \(f_1\)を横軸、\(f_2\)を縦軸にとりグラフにすると図2(薄い赤の部分)のように\(f_1,\;f_2\)の安定領域を表せる。