25. 最適レギュレータ
現代制御理論における最適レギュレータは、制御対象の状態を評価関数と呼ばれる指標に基づいて最適な状態に導く制御システムで、状態フィードバックを用いて制御し、評価関数の最小値となるようなフィードバックゲインを決定することで実現する。最適レギュレータは、以下の要素で構成される。
・制御対象: 制御対象となるシステムは状態方程式で表される。
・評価関数: システムの状態を評価する指標で、状態の2乗和や制御入力の2乗和などを用いる。
・状態フィードバック: システムの状態量をフィードバックする。
・フィードバックゲイン:状態フィードバックの重み付け係数。
最適レギュレータは、以下の利点がある。
・システムの安定性を保証できる: 評価関数の最小値となるようなフィードバックゲインを設計することで、システムの安定性を保証できる。
・望ましい応答性能を実現できる:評価関数を適切に設定することで、システムの応答速度、過渡特性、定常誤差などの望ましい応答性能を実現できる。
外部ノイズの影響に強い:状態フィードバックを用いることで、外部ノイズの影響を受けにくい制御システムを実現できる。
最適レギュレータ問題
制御対象の状態方程式を$$\dot{x}(t) = A x(t) + b u(t) , \;\;\;x(0) = x_0 \\ y(t) = c x(t) \;\;\;\;\;\;\;\;\;\;\;\; \cdots \cdots(1)$$とする。なお、\(x(t),u(t),y(t)\)は時間の関数として、以降\((t)\)の表記を省略する。
評価関数を次の2次形式で表す。$$J = \int_0^{+\infty} \left(x^{T}Q x + r u^2 \right) dt \;\;\;\; \cdots (2)$$ ここで、\(Q \in R^{n \times n}\)は正定対称行列、\(Q \gt 0\)、\(r \in R^{1 \times 1}\)を正の数とする。この\(J\)を最小とする入力\(u, \;\;\; t \in [0, +\infty)\)を求める。これが最適レギュレータ問題である。
評価関数\(J\)は操作入力\(u\)のエネルギーと状態ベクトル\(x\)のエネルギーの和を時間区間\([0, +\infty)\)で積分したものとなっている。式(2)の2次形式評価関数\(J\)の第1項の積分は、システムの状態ベクトルの原点への収束の速さの指標であり、第2項は、状態ベクトルを原点へ収束させるために必要な操作入力\(u\)のエネルギーを表している。なお、\(Q = c c^T\)とすれば、第1項は出力\(y\)の指標となる。状態ベクトルの原点への収束を速くしようとすると、大きな操作入力エネルギーが必要となり、\(J\)の第2項が大きくなる。逆に操作入力エネルギーを小さくすると、状態ベクトルの原点への収束が遅くなるので、\(J\)の第1項が大きくなる。このように最適レギュレータの評価関数\(J\)の第1項と第2項はトレードオフの関係にある。操作入力エネルギーと状態ベクトルの原点への収束速さのどちらに重きを置くかは、制御システム設計者の判断に委ねられる。正定行列\(Q\)を固定して考えると、操作入力エネルギーを小さくしたい場合は、\(r \gt 0\)の値をより大きく、状態ベクトルの原点への収束を重視する場合は、\(r\)の値をより小さくとれば良いことになる。
最適レギュレータ問題の解
式(1)の制御対象において、\((A,b)\)は可制御とする。このとき、式(2)の評価関数\(J\)を最小にする入力\(u\)は、状態フィードバック$$u = -f x \;\;\;\; \cdots (3)\\ f = r^{-1} b^T P \;\;\;\; \cdots (4)$$で与えられる。\(P\)はリッカチ行列方程式$$A^T P + PA + Q - r^{-1}P b b^T P = 0 \;\;\;\; \cdots (5)$$を満たす正定対称行列である。このとき、評価関数\(J\)の最小値は、$$J_{min} = x(0)^T P x(0)$$となる。
これは、最適レギュレータ問題の解が状態フィードバックで与えられることを示しており、制御対象が不安定であっても、最適レギュレータは状態フィードバックにより制御対象を安定化できることも意味している。
最適レギュレータの解(式(3),(4))の必要条件
操作入力\(u\)に状態フィードバック\(u = -fx\)と仮定すると、状態方程式、評価関数\(J\)として、$$\dot{x} = (A - bf) x , \;\; x(0) = x_0 = 0 \\ y = cx \;\;\;\;\;\;\; \cdots \cdots (6)$$ $$J = \int_0^{+\infty} x^T ( Q + r f^T f)x dt \;\;\;\;\; \cdots (7)$$を得る。\(J\)が有限な確定値をとるためには、\(\lim_{t \rightarrow +\infty} x=0\)とならなければならない。\((A,b)\)は可制御なので、\(A - bf\)を安定とする\(f\)が存在する。\(A - bf\)が安定行列ならば、正定対称行列\(Q + rf^Tf \gt 0\)に対して、リヤプノフの行列方程式$$(A - bf)^T P + P(A - bf) = - (Q + rf^T f) \;\;\;\; \cdots (8)$$を満たす正定対称行列\(P \gt 0\)が存在する。このとき、正定対称行列\(P\)はフィードバックゲインベクトル\(f\)の関数と見なせる。式(7)の評価関数\(J\)の式に式(8)のリヤプノフの行列方程式を代入すると、評価関数\(J\)は正定対称行列\(P\)の関数として以下のように表せる。
$$J = - \int_0^{+\infty} x^T\left[(A - bf)^T P + P(A - bf)\right]x dt \\ = - \int_0^{+\infty} \left\{ \frac{d x^T}{dt} P x + x^T P \frac{dx}{dt} \right\}dt \\ = -\int_0^{+\infty} \frac{d}{dt} \left\{ x^T Px \right\} dt \\ = -x( + \infty)^T P x(+ \infty) + x(0)^T P x(0) \\ = x(0)^T P x(0) $$
リヤプノフの定理
どのような \(Q \gt 0\)に対しても、\(A^T P + P A + Q =0\)を満たす\(P \gt 0\)が一意的に存在するための必要十分条件は、線形常微分方程式 \(\dot{x} = A x \) が大域的に漸近安定であることである。
この\(J\)を最小にするフィードバックゲインベクトル\(f\)の必要条件は、\(J\)を\(f\)の各要素\(f_i\)で偏微分したとき、すべての要素\(f_i\)に対して、$$\frac{\partial J}{\partial f_i} = x(0)^T \left( \frac{\partial P}{\partial f_i}\right) x(0) = 0 , \;\;\;\; i=1,2,\cdots . n \;\;\;\; \cdots (9)$$となることである。式(9)の状態ベクトル\(x\)の初期値\(x(0)\)は零でない任意の定数ベクトルなので、$$\frac{\partial P}{\partial f_i} = 0, \;\;\;\; i=1,2,\cdots . n \;\;\;\; \cdots (10)$$となる。ここで、式(8)のリヤプノフの行列方程式の両辺を\(f_i\)で偏微分すると、正定対称行列\(P\)はフィードバックゲインベクトル\(f\)の関数なので、$$\left\{ \frac{\partial(A - b f)^T}{\partial f_i} \right\} P + (A - b f)^T \frac{\partial P}{\partial f_i} + \left(\frac{\partial P}{\partial f_i} \right) (A - b f) + P \frac{\partial(A - b f)}{\partial f_i} = - \frac{\partial (Q + r f^T f)}{\partial f_i} $$を得る。これに式(10)を代入すると$$\left\{ \frac{\partial(A - b f)^T}{\partial f_i} \right\} P + P \frac{\partial(A - b f)}{\partial f_i} = - \frac{\partial (Q + r f^T f)}{\partial f_i} $$となり、これは$$\left(\frac{\partial f^T}{\partial f_i}\right) b^T P + Pb\left(\frac{\partial f}{\partial f_i}\right) = r \left\{\left(\frac{\partial f^T}{\partial f_i}\right)f + f^T\left(\frac{\partial f}{\partial f_i}\right) \right\} \;\;\;\; i=1,2, \cdots, n \;\;\;\; \cdots (11)$$である。式(11)は、行ベクトル\(b^T P\)の第\(i\)要素は、行ベクトル\(r f\)の第\(i\)要素に等しく、列ベクトル\(P b\)の第\(i\)要素は列ベクトル\(r f^T\)の第\(i\)要素に等しいことを示している。よって、\(b^T P = rf\)が成立し、式(4)のフィードバックゲインベクトル$$f = r^{-1} b^T P$$が得られる。この結果を式(8)のリヤプノフの行列方程式に代入すると、式(5)のリッカチ行列方程式を得る。
以上が、最適レギュレータの解(式(3),(4))の必要条件である。十分条件に関しては省略する。
連続時間リッカチ行列方程式の解法(クラインマンの方法)
連続時間系の最適レギュレータ問題を解くには、式(5)の連続時間リッカチ行列方程式を解かなければならない。その解法の一つとしてクラインマンの方法がある。
1)\((A,b)\)は可制御とする。フィードバックゲインベクトル\(f\)の初期値を\(f_0\)として、\(A-bf_0\)が安定となるように任意の\(f_0\)を設定する。
2)\(i=0\)として、リヤプノフの行列方程式$$(A - bf_i)^T P_i +P_i(A - bf_i) = -(Q + r f_i^T f_i)$$を満足する正定対称行列\(P_i\)を求める。
3)\(P_i\)を使って、新しいフィードバックゲインベクトル\(f_{i+1}\)を$$f_{i+1} = r^{-1} b^T P_i$$と置き、\(i \rightarrow i+1\)として、2)に戻る。
以上の操作を繰り返すと、\(P_i\)は\(i \rightarrow +\infty\)において、解\(P\)に収束する。この\(P\)を用いて、最適なフィードバックゲインベクトル\(f\)を求める。
最適レギュレータの設計例
制御対象の状態方程式を$$\dot{x} = \begin{bmatrix} 2 & 1 \\ 0 & 1 \end{bmatrix} x + \begin{bmatrix} 1 \\ 2 \end{bmatrix} u , \;\;\;\;\; x(0) = \begin{bmatrix} 10 \\10 \end{bmatrix}$$としたとき、評価関数$$J = \int_0^{\infty} \left\{x^T \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} x + 1\cdot u^2 \right\} dt $$を最小にする入力\(u\)を求める。
$$ A = \begin{bmatrix} 2 & 1 \\ 0 & 1 \end{bmatrix} , \;\;\; b = \begin{bmatrix} 1 \\ 2 \end{bmatrix} , \;\;\; Q = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} , \;\;\; r =1$$より、リッカチ行列方程式は、$$\begin{bmatrix} 2 & 1 \\ 0 & 1 \end{bmatrix} ^T P + P \begin{bmatrix} 2 & 1 \\ 0 & 1 \end{bmatrix} - P \begin{bmatrix} 1 \\ 2 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix}^T P = - \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$$となる。このときの正定値解は、$$P = \begin{bmatrix} 8.1003468 & -1.1604767 \\ -1.1604767 & 0.9798406 \end{bmatrix} $$となるので、フィードバックゲインベクトル\(f\)は、$$f = r^{-1} b^T P = \begin{bmatrix} 5.7793933 & 0.7992044 \end{bmatrix}$$となる。
なお、一般のシステムでは、システム行列\(A\)の次元は3以上の場合が多いので、これらの計算は、Scilab、Matlabなどの数値解析ソフトを使用することになる。
以下にScilabによる数値計算と状態ベクトルのグラフなどの例を示す。
Scilab スクリプト
//25. 最適レギュレータ
clear;clf();
i=%i;
//制御対象システムの定義
A=[2 1; 0 1];
b=[1; 2];
c=[1 0 ; 0 1];
x0 = [10;10]; /* 初期状態変数*/ sysP=syslin('c',A,b,c);
//制御対象の固有値
evals=spec(A);
//可制御性のチェック
Uc=cont_mat(A,b);
n=rank(Uc);
//重み係数
Q=[1 0; 0 1]; r=1;
//状態フィードバック係数の決定 P=riccati(A,binv(r)b',Q,'c','eigen');
f=inv(r)b'P
cpoles=spec(A-bf); //極配置の確認
//制御対象の時間応答
t=0:0.01:3;
deff('u=timefun(t)','u=0')
y0=csim(timefun,t,sysP,x0);
scf(0); plot(t',y0');
//最適レギュレータの時間応答
A2=A-b*f;
sysP2=syslin('c',A2,b,c);
y=csim(timefun,t,sysP2,x0);
scf(1); plot(t',y');
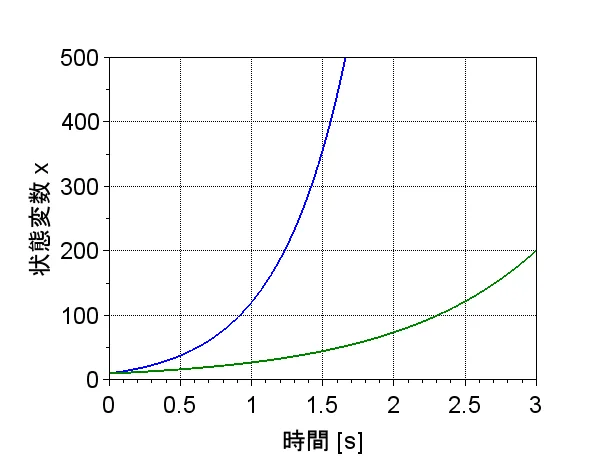
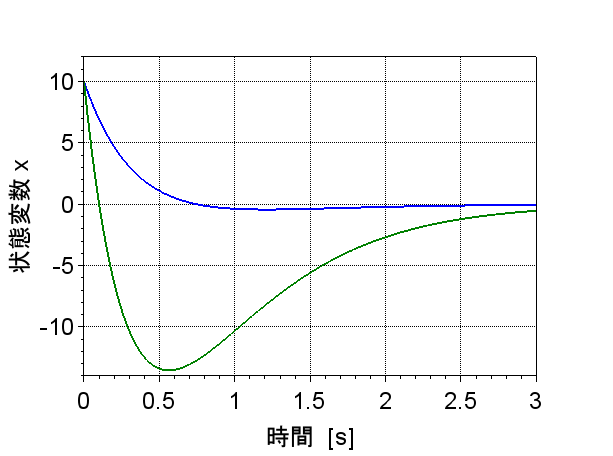
図1は、制御対象の時間応答である。状態変数\(x\)が時間とともに発散しており、不安定なシステムであることが分かる。図2は状態フィードバックによる最適レギュレータを実現した時間応答である。状態変数\(x\)が初期値\(x(0) = \begin{bmatrix} 10 \\10 \end{bmatrix}\)から時間とともに零に収束しており、安定なシステムが実現できていることが分かる。


“25. 最適レギュレータ” に対して2件のコメントがあります。
コメントは受け付けていません。