14. IIRディジタルフィルタ
IIR(Infinite Impulse Response)ディジタルフィルタの設計では、確立しているアナログフィルタの設計理論を利用する。まず、アナログフィルタの伝達関数\(G(s)\)を設計し、その後何らかの変換法を利用して、ディジタルフィルタの伝達関数\(G(z)\)を求めるという方法が一般的である。
代表的なアナログフィルタのタイプとして、バタワースフィルタ、チェビシェフフィルタがある。以下に振幅特性の概要をまとめる。
バタワースフィルタ
バタワースフィルタの振幅特性は、$$|G(j\omega)| =\frac{1}{\sqrt{1 + (\omega / \omega_c)^{2N}}}$$である。また、二乗振幅特性は、$$|G(j\omega)| ^2=\frac{1}{1 + (\omega / \omega_c)^{2N}}$$となる。図1は遮断角周波数\(\omega_c =1\)に設定したときの二乗振幅特性のグラフである。遮断角周波数\(\omega_c=1\)において、二乗振幅が\(0.5\)となる。つまり、振幅特性で考えると\(\frac{1}{\sqrt{2}}\)(-3 dB)である。
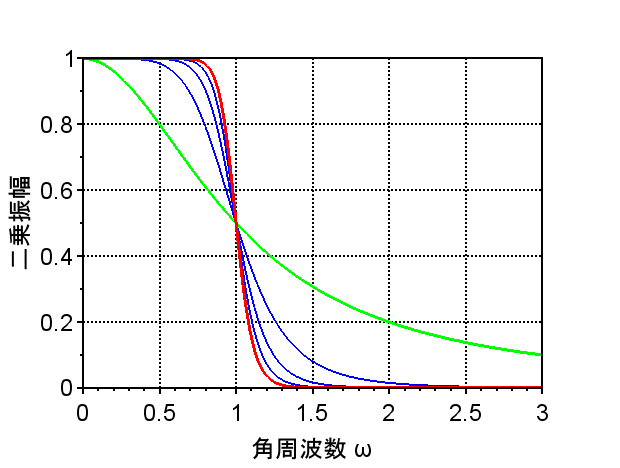
緑線が\(N=1\)のとき、赤線が\(N=9\)としたときの特性である。このように、\(N\)を大きくすると、理想低域フィルタの特性(遮断角周波数を境に通過、遮断が明確に分かれる)に近づくことが分かる。
チェビシェフフィルタ
チェビシェフフィルタは、通過域に等リップル特性をもっており、振幅特性は、$$|G(j \omega)| =\frac{1}{\sqrt{1 + \epsilon^2 \{C_N (\omega/ \omega_c)\}^2}}$$で与えられる。ここで、\(C_N(\omega / \omega_c)\)は\(N\)次のチェビシェフ多項式で、等リップル特性は、この多項式の性質による。また、\(\epsilon\)は通過域のリップルの大きさに関するパラメータである。
\(N\)次のチェビシェフ多項式\(C_N\)は、$$C_N(\omega) = \begin{cases} \cos(N \cos^{-1} \omega), & |\omega| \leq 1 \\ \cosh(N \cosh^{-1} \omega) , & |\omega| \gt 1 \end{cases}$$で表せる。
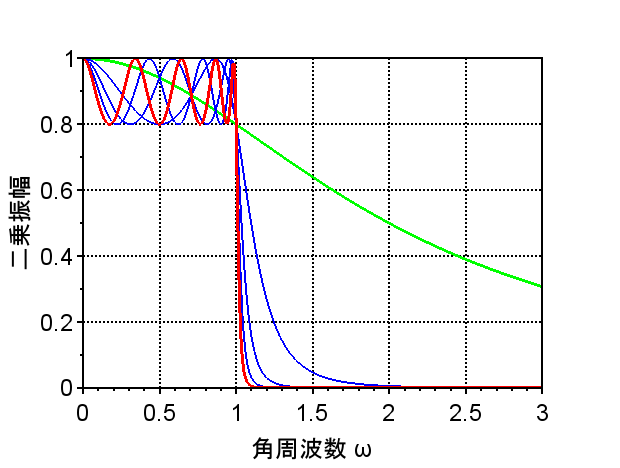
なお、二乗振幅特性は、$$|G(j \omega)|^2 =\frac{1}{1 + \epsilon^2 \{C_N (\omega/ \omega_c)\}^2}$$となる。図2は遮断角周波数\(\omega_c =1\)、リップルの大きさ\(\epsilon = 0.5\)に設定したときの二乗振幅特性のグラフである。緑線が\(N=1\)のとき、赤線が\(N=9\)としたときの特性である。\(N\)を大きくすると、理想低域フィルタの特性(遮断角周波数を境に通過、遮断が明確に分かれる)に近づくのは、バタワースフィルタと同様であるが、\(N\)が大きくなるとバタワースフィルタよりチェビシェフフィルタの方が減衰特性は急峻となる。
図1、図2を描画するためのScilabスクリプトを以下に示す。
//14. アナログフィルタの特性
clear; clf();
wc=1; /遮断角周波数/
w=0:0.01:3; /角周波数範囲/
//バタワースフィルタ 2乗振幅特性
for N=1:2:10
G1 = buttmag(N,wc,w); /2乗振幅の計算/
scf(0); plot(w, G1);
end;
//チェビシェフフィルタ 2乗振幅特性
eps=0.5; /*リップの大きさ */
for N=1:2:10
G2 = cheb1mag(N,wc,eps,w); /2乗振幅の計算/
scf(1); plot(w,G2);
end
双一次変換法
アナログフィルタの伝達関数\(G(s)\)からディジタルフィルタの伝達関数\(G(z)\)を求める代表的な手法として双一次変換法がある。安定なアナログフィルタの伝達関数\(G(s)\)を安定なディジタルフィルタの伝達関数\(G(z)\)に変換するには、\(s\)平面と\(z\)平面の対応が1対1で、\(s\)平面の安定領域が\(z\)平面の安定領域に変換さればよい。つまり、\(s\)平面の虚軸が\(z\)平面の単位円になり、\(s\)平面の左半平面が\(z\)平面の単位円内に対応するような変換法であればよい。この変換法として、双一次変換法がある。
双一次変換法は、$$s = \frac{2}{T} \cdot \frac{1-z^{-1}}{1+z^{-1}}$$を使って、ディジタルフィルタの伝達関数\(G(z)\)を得る。$$G(z) = G(s)|_{s=(2/T)\cdot \left(1-z^{-1} \right) / \left(1+z^{-1} \right) } = G\left(\frac{2}{T} \cdot \frac{1-z^{-1}}{1+z^{-1}} \right)$$
双一次変換法の誘導
式(1)の双一次変換式は以下のように考える。図3に示すように、信号を\(x(t)\)とすると、\(x(t)\)の\(t=nT\)までの積分値\(y(n)\)は、$$y(n) = \int_0^{nT} x(t) dt $$であり、図3の赤斜線の部分、すなわち、サンプリング周期\(T\)に対する面積は、$$y(n) - y(n-1) = \int_{(n-1)T}^{nT} x(t) dt$$で与えられる。
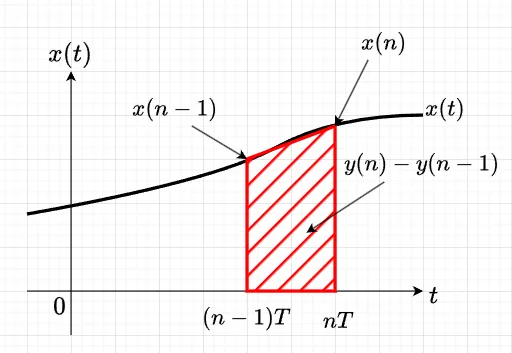
\(x(t)\)のサンプル値を\(x(n)\)として、赤斜線部分の面積を台形に近似すると、$$y(n) -y(n-1) = \frac{x(n) + x(n-1)}{2}T$$となる。この式をZ変換すると、$$(1 -z^{-1})Y(z) = \frac{T}{2} (1+z^{-1})X(z)$$なので、ディジタル積分演算子は、$$\frac{Y(z)}{X(z)} = \frac{T}{2} \cdot \frac{1+z^{-1}}{1-z^{-1}}$$となる。一方、アナログの積分演算子は、\(1/s\)であるから、$$\frac{1}{s} = \frac{T}{2} \cdot \frac{1+z^{-1}}{1-z^{-1}}$$である。よって、$$s = \frac{2}{T} \cdot \frac{1-z^{-1}}{1+z^{-1}}$$の関係が得られる。台形に近似したことから分かるように、サンプリング周期\(T\)が小さければ、この変換は妥当であるが、\(T\)が大きくなると歪(変換誤差)が大きくなる。
式(1)の変換式は、図4に示すように\(s\)平面の左半平面を\(z\)平面の単位円内に写像する。アナログフィルタの安定条件は、全ての極が\(s\)平面の左半平面に存在することであり、ディジタルフィルタの安定条件は、全ての極が単位円内に存在することである。従って、双一次変換によって得られたディジタルフィルタは、元となるアナログフィルタが安定であれば、常に安定となる。
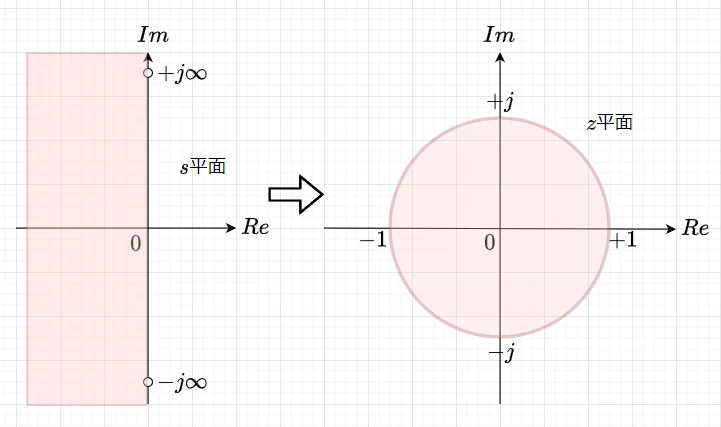
しかしながら、双一次変換法では、先に述べたようにサンプリング周期\(T\)により、アナログとディジタルの周波数軸にひずみを生じる(\(s\)平面の虚軸(直線)が、\(z\)平面の単位円(円周)に写像される。)。アナログの周波数を\(\omega_a\)、ディジタルの周波数を\(\omega_d\)として、\(s=j\omega_a\)、\(z = e^{j \omega_d T} \)の関係を式(1)に代入し、オイラーの公式を使うと、$$ j \omega_a = \frac{2}{T} \cdot \frac{1 - e^{-j \omega_d T}}{1 + e^{-j \omega_d T}} \\ =\frac{2}{T} \cdot \frac{1 - (\cos \omega_d T - j \sin \omega_d T)}{1 + (\cos \omega_d T - j \sin \omega_d T)} \\= \frac{2}{T} \cdot j \frac{\sin \omega_d T}{1 + \cos \omega_d T} = \frac{2}{T} \cdot j \tan \frac{\omega_d T}{2} $$のように式整理できる。よって、$$\omega_a = \frac{2}{T} \cdot \tan \frac{\omega_d T}{2} , \;\;\;\;\; \frac{\omega_a T}{2} = \tan \frac{\omega_d T}{2} $$である。つまり、\(\omega_a\)と\(\omega_d\)は非線形の関係にある。
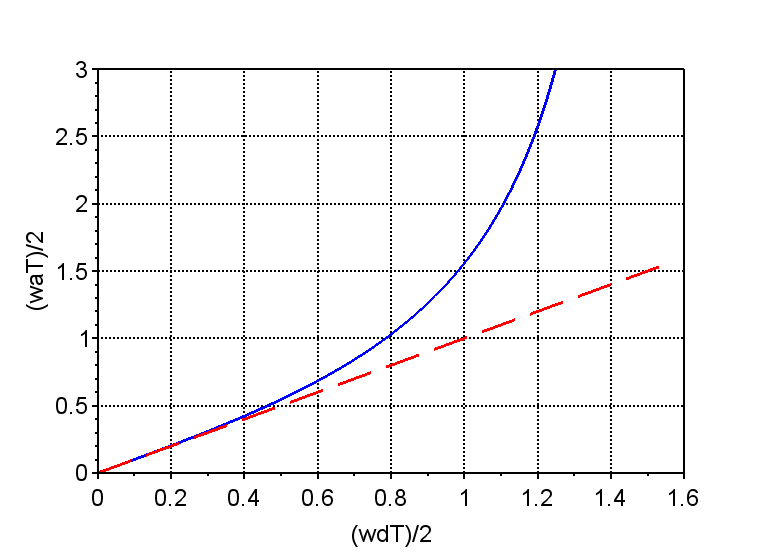
図5は、横軸を\(\frac{\omega_d T}{2}\)、縦軸を\(\frac{\omega_a T}{2}\)にし、双一次変換法の周波数ひずみを表したグラフ(青線)である。このグラフより、\(\frac{\omega_a T}{2} \lt \pi/8 \approx 0.4\)以下の領域であれば、\(\omega_a\)と\(\omega_d\)は、ほぼ線形(赤破線)の関係にあるが、それ以上の領域では、非線形の影響が大きくなることがわかる。このように、ディジタルフィルタを設計する際には、この周波数のひずみを考慮して設計する必要がある。
双一次変換によるIIRディジタルフィルタの設計例
*一次系のディジタルフィルタ
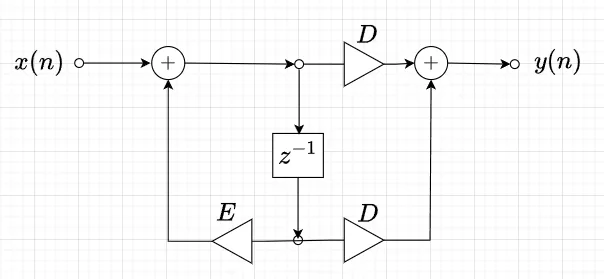
1次系の連続時間伝達関数を$$G(s) = \frac{R}{s + R}$$とする。これにサンプリング周期を\(T\)として双一次変換を適用すると、$$G(z) = \frac{R}{\frac{2}{T} \cdot \frac{1 - z^{-1}}{1 + z^{-1}} + R} = \frac{RT(1+z^{-1})}{2(1-z^{-1}) + RT(1 + z^{-1})} \\ = \frac{\frac{RT}{2+RT}(1+z^{-1})}{1- \frac{2-RT}{2+RT}z^{-1}} = \frac{D(1+z^{-1})}{1-Ez^{-1}}$$ただし、$$D = \frac{RT}{2+RT}, \;\;\; E = \frac{2-RT}{2+RT}$$である。\(G(z)=\frac{Y(z)}{X(z)}\)より、$$Y(z) = G(z)X(z) = \frac{D(1+z^{-1})}{1-Ez^{-1}} X(z)$$なので、$$Y(z)(1 - Ez^{-1}) = D(1 + z^{-1}) X(z)$$これを逆Z変換すると、$$y(n) - Ey(n-1) = Dx(n) + Dx(n-1) , \;\;\; y(n) = Dx(n) + Dx(n-1) + Ey(n-1)$$の演算で実現できることが分かる。図6に1次系ディジタルフィルタの構成図を示す。
IIRフィルタの構成
\(N\)次IIRフィルタの伝達関数を以下の式(1)のように同次数の分母多項式\(D(z)\)と分子多項式\(N(z)\)の比の形で与えられたとする。$$G(z) = \frac{N(z)}{D(z)} = \frac{\sum_{k=0}^N a_k z^{-k}}{1 + \sum_{k=1}^N b_k z^{k-1}}\;\;\;\; \cdots (1)$$ここで、入力を\(X(z)\)、出力を\(Y(z)\)とすると、\(Y(z) = G(z) X(z)\)より、$$Y(z)\left(1 + \sum_{k=1}^N b_k z^{k-1}\right) = X(z)\left(\sum_{k=0}^N a_k z^{-k}\right)$$なので、これを逆Z変換することで式(1)の時間領域表現は、入力\(x(nT)\)、出力\(y(nT)\)として、$$y(nT) = \sum_{k=0}^N a_k x(nT - kT) - \sum_{k=1}^N b_k y(nT - kT) \;\;\;\; \cdots (2)$$となる。
1)直接型Ⅰ
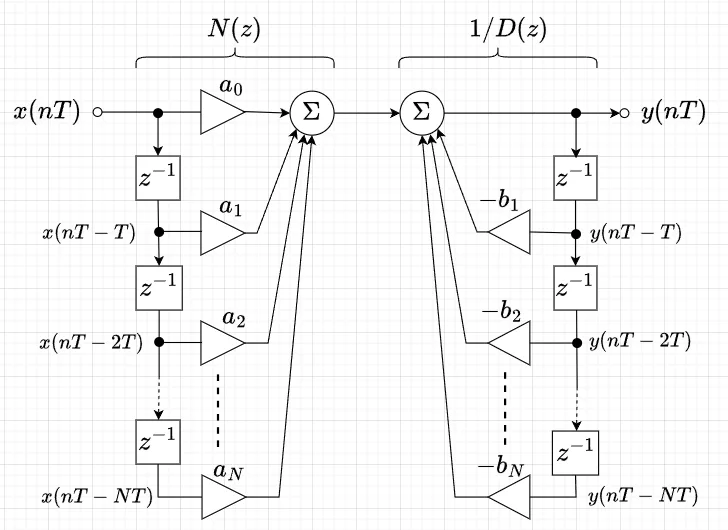
式(2)を直接にブロック図で表すと、図7に示す直接型Ⅰと呼ばれる構成となる。
図より、$$N(z) = \sum_{k=0}^N a_k z^{-k} \\ \frac{1}{D(z)} = \frac{1}{ 1 + \sum_{k=1}^N b_k z^{k-1}}$$で、伝達関数\(G(z)\)の分子\(N(z)\)を構成し、分母\(1/D(z)\)を縦続接続することで実現している。$$G(z) = N(z) \left(\frac{1}{D(z)}\right)$$
ここで、\(z^{-1}\)は遅延子である。
2)直接型Ⅱ
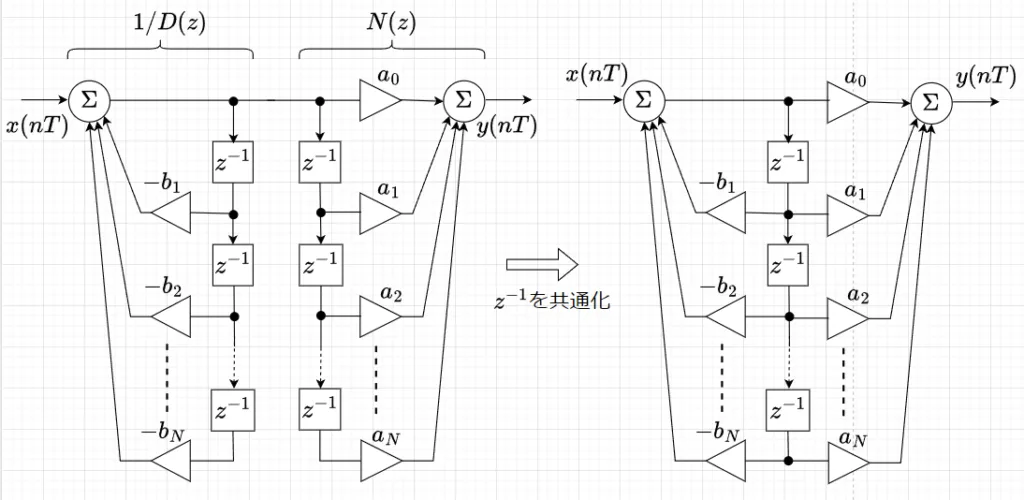
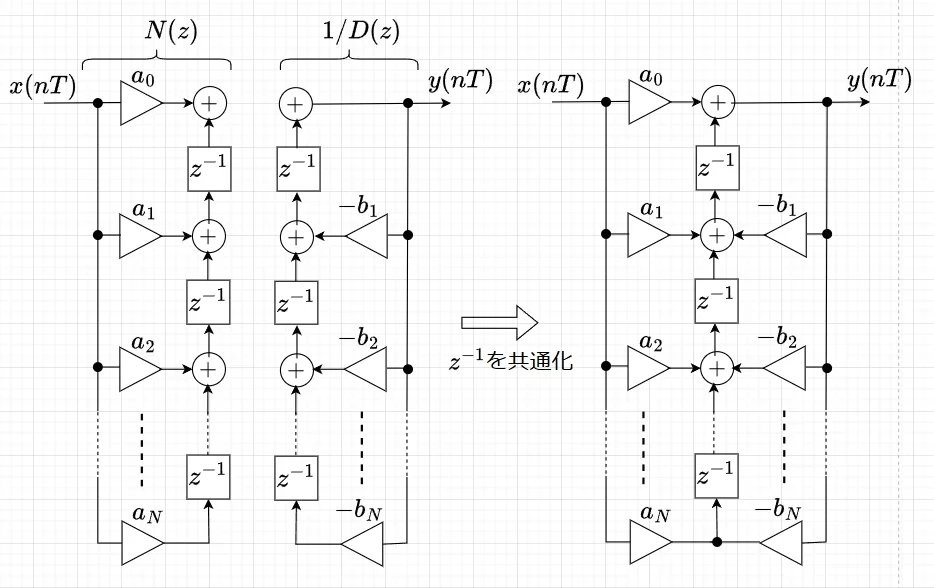
\(G(z)\)は線形演算で、$$G(z) = \left(\frac{1}{D(z)}\right) N(z)$$とすることができるので、図8左図に示すように、図7における\(1/D(z)\)と\(N(z)\)の演算の順序を入れ換えた構成が可能である。さらに、遅延子\(z^{-1}\)を共有化すると、図8の右図のような構成になる。この構成を直接型Ⅱと呼ぶ。本構成は、遅延子の数が最小になることが知られている。
3)直接型Ⅱの転置型
$$N(z) = \sum_{k=0}^N a_k z^{-k} = a_0 + z^{-1}(a_1 + z^{-1}(a_2 + \cdots + z^{-1}(a_{N-1} + z^{-1}a_N)) \cdots )$$と変形できる。\(D(z)\)も同様に変形できるので、構成図は図9のように描ける。この構成は、直接型Ⅱの前後構成を転置したようになっているので、直接型Ⅱの転置型構成と呼ばれる。
Biquad回路の縦続構成
高次伝達関数のIIRディジタルフィルタをディジタル回路で実装する場合、一般的には、Biquad回路の縦続接続、並列接続で実現する。IIRディジタルフィルタの伝達関数\(G(z)\)は、1次及び2次(Biquad回路)の縦続型として求めることができる。1次は2次の場合の\(a_{2k},b_{2k}\)の係数を零とすれば実現できるので、\(G(z)\)はBiquad回路の縦続のみで表すことができる。つまり伝達関数の次数を\(N\)次とすれば、$$G(z) = G_0 \prod_{k=1}^L \frac{a_{2k}z^{-2} + a_{1k} z^{-1} + a_{0k}}{b_{2k} z^{-2} + b_{1k} z^{-1} + 1} \;\;\;\; \cdots (3)$$ただし、$$L = \begin{cases} N/2 & N:偶数 \\ (N+1)/2 & N:奇数 \end{cases}$$である。
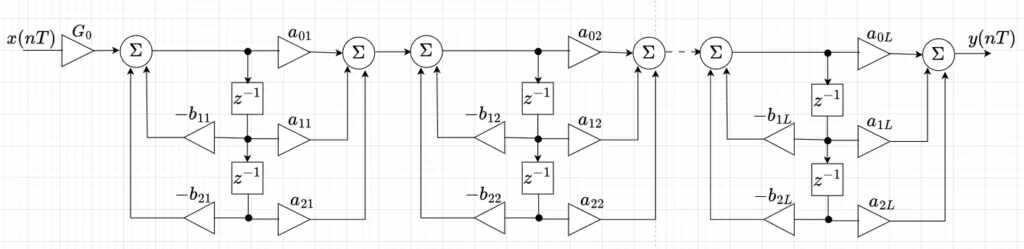
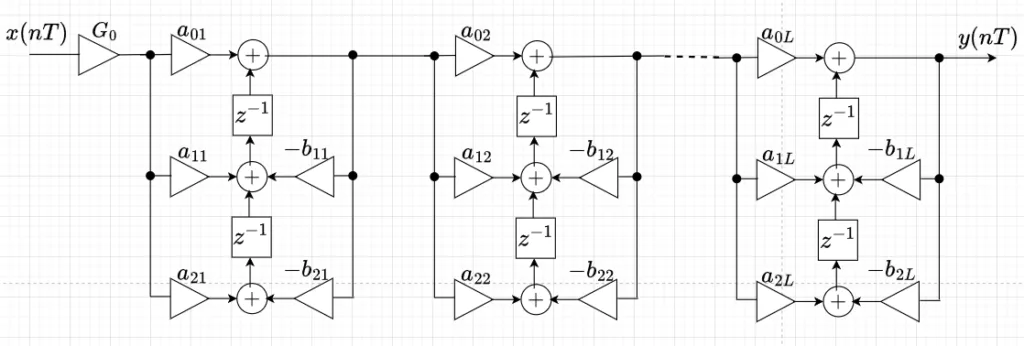
Biquad回路を直接型Ⅱで構成したものを1Dタイプ(図10)、直接型Ⅱの転置型で構成したものを2Dタイプ(図11)と呼ぶ。
Biquad回路の並列構成
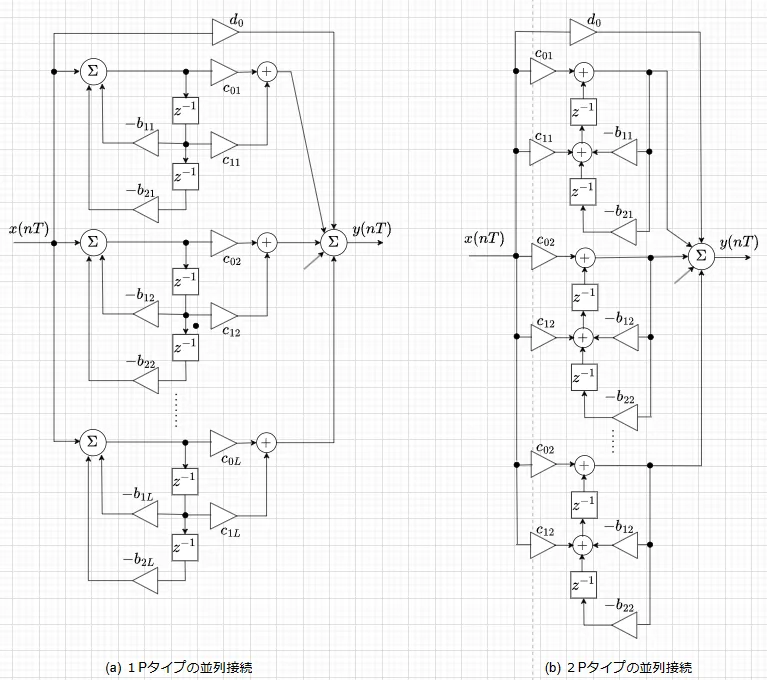
IIRディジタルフィルタの伝達関数\(G(z)\)は、部分分数に分解すれば、式(4)のように総和の形で表せる。$$G(z) = d_0 + \sum_{k=1}^L \frac{c_{1k}z^{-1} + c_{0k}}{b_{2k}z^{-2} + b_{1k}z^{-1} +1} \;\;\;\; \cdots (4)$$ ただし、$$L = \begin{cases} N/2 & N:偶数 \\ (N+1)/2 & N:奇数 \end{cases}$$である。第2項は、2次伝達関数の総和なので式(4)の\(G(z)\)は、Biquad回路の並列接続で構成できる。各Biquad回路を直接型Ⅱで構成した図12(a)の回路構成を1Pタイプ、直接型Ⅱの転置型で構成した図12(b)の回路構成を2Pタイプと呼ぶ。1次伝達関数は、Biquad回路の一つについて係数\(b_{2k},\; c_{1k}\を零にすれば実現できる。
並列接続構成の特徴は、縦続接続構成と比較して以下となる。
(1)分子項の\(z^{-2}\)の項が無いので、乗算器(乗算演算)が各Biquadにつき1個減る。
(2)各Biquad回路は、入力信号が同一なので、並列処理が簡単にできる。
(3)縦続接続に比べて、一般的に発生雑音が低減される。
とくに(2)の特徴は、並列処理により処理可能周波数帯域を高くできることを意味する。

