3. 初等関数(微積分学)
初等関数(elementary function)とは、数学において基本的でよく知られた関数の総称で、以下のような関数が初等関数として挙げられる。
1.多項式関数(代数関数)(例:\( f(x) = x^2 + 3x + 2\))
2.指数関数・対数関数(例: \(f(x) = e^{x},\;f(x) = \log(x)\))
3.三角関数(例: \(f(x)=\sin(x), \; \cos(x),\; \tan(x)\))
4.逆三角関数(例: \(f(x) = \arcsin(x),\; \arccos(x),\; \arctan(x)\))
初等関数は、複雑な関数を表現するための基本的な要素として使用される。
多項式関数
\(x\)の多項式とは、変数\(x\)の自然数べき乗の定数倍の項を有限個と定数項を足し合わせた式である。$$f(x) \equiv a_0 x^n + a_1 x^{n-1} + \cdots + a_{n-1} x + a_n \\ \equiv \sum_{k=0}^n a_k x^{n-k}$$ \(a_0 \neq 0\)ならば、\(n\)を多項式\(f(x)\)の次数と呼ぶ。なお、\(x=0\)の場合も含めて\(x^0 \equiv 1\)とする。
関数の定義
一個(または複数)の変数\(x\)があり、それがとる値に応じて変数\(y\)がとる値を計算できる数式が与えられたとき、その関係式を関数と呼ぶが、より一般的な関数の定義は、「空でない集合\(X\)と集合\(Y\)が与えられたとするとき、任意の\(x \in X\)に対してただ1つの\(y \in Y\)が定まるならば、\(y\)を\(x\)の関数という。」である。つまり、写像\(f:x \mapsto y\)が関数\(y=f(x)\)である。
※多価関数などが含まれていない狭義の定義であることに注意。
多項式関数(代数関数)
多項式の比で表す関数を有理関数という。$$f(x) = \frac{N(x)}{D(x)}$$\(N(x),\;D(x)\)は、\(x\)の多項式で、\(D(x)\)は零にならない多項式とする。\(f\)の定義域は、分母多項式\(D(x)\)が零とならない全ての\(x\)から成る。
\(x\)の負べき乗\(x^{-n}\)は、逆数\(1/x\)の正べき乗\(1/x^{n}\)である。また分数べき乗\(x^{1/n}\)は、べき根\(\sqrt[n]{x}\)と同じである。
2変数の多項式\(P(x,y)\)において、方程式\(P(x,y)=0\)の解\(y\)を\(x\)の代数関数という。代数関数でない関数(指数関数や三角関数など)を超越関数という。
一般に\(y\)をあらわに\(x\)で表さずに、方程式の解として定義する関数を陰関数という。
指数関数・対数関数
べき乗は、加法定理\(a^p a^q = a^{p+q}\)とべき乗則\((a^p)^q = a^{pq}\)を満たす。これは、\(p,\;q\)が有理数のときは簡単に確かめられるが、実数の連続性を使って実数の場合にも成立するように拡張できる。
指数関数は、べき乗の指数の方を変数と考えた関数である。\(x\)を実数として、その指数関数\(a^x\)を以下のように定義する。$$\lim_{n \rightarrow \infty} \left( 1 + \frac{x}{n}\right)^n \equiv e^x \equiv \exp x \;\;\; \cdots (1)$$ここで、\(e\)は、式(1)の\(x=1\)の値(\(e = 2.71828 \cdots\))で、自然対数の底、または、ネイピア数と呼ばれる。
指数関数の逆関数を対数関数という。\(y = e^x\)のとき、\(x = \log y\)、または、\(y= \ln x\)と表し、自然対数と呼ぶ。\(e^{\log a} = a \)なので、\(a^x = e^{x \log a}\)である。
※以上は、\(a \gt 0\)を仮定しているが、\(a \lt 0\)を正しく含めるには、全てを複素数に拡張しなければならない。
三角関数・逆三角関数
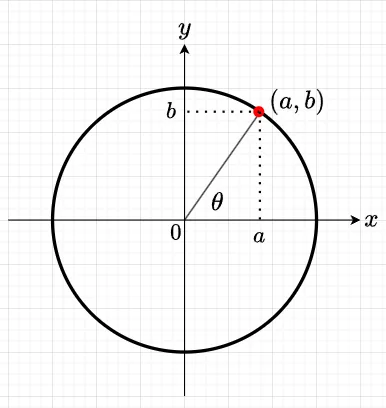
三角関数の定義は、図1のように、直交座標系における単位円(半径1の円)の座標(\(a,b\))を極座標で表し、$$a = \cos \theta, \;\;\;\;\; b = \sin \theta\\ \frac{b}{a} = \frac{\sin \theta}{ \cos \theta} = \tan \theta $$である。単位円の方程式\(a^2 + b^2 = 1\)は、\(\cos^2 \theta + \sin^2 \theta =1\)となる。この定義から、\(\cos \theta\)と\(\sin \theta\)が\(2 \pi\)を周期とする周期関数であることがわかる。ただし、\(\tan \theta\)の周期は、\(\pi\)になる。
\(\sin \theta\)と\(\tan \theta\)は奇関数、\(\cos \theta\)は偶関数である。\(\theta = n \pi\)(\(n\):整数)のとき、\(\sin \theta = 0\)、また、\(\cos \theta = \sin(\pi/2 \pm \theta)\)の関係である。
三角関数の逆関数が逆三角関数で、\(\sin \theta\)の逆関数は、\(\arcsin\)または、\(\sin^{-1}\)と書く。他の逆三角関数も同様とする。三角関数は周期関数なので、逆三角関数の値は一意に決まらず、無限多値となる。
代数関数に指数関数、対数関数、三角関数、逆三角関数を組み合わせて構成できる関数を初等関数という。なお、初等関数では表せないが、応用上大切な関数は多く存在する。

