5. 積分(微積分学)
積分の定義は、微分の逆演算と関数のグラフをヒストグラムの極限と見た時の面積という2つの面がある。
※微小量、微分の記法などについては、 4. 微分(微積分学)を参照願います。
微分の逆演算としての積分
\(F(x)\)の導関数(\(F(x)\)を微分したもの)が\(f(x)\)に等しい時、前者を後者の原始関数(もしくは不定積分)といい、$$F(x) = \int f(x) dx$$と書く。定数の微分は\(0\)、また、定数でない関数の微分は\(0\)にならない。よって、\(F(x)\)は付加定数の分だけ決まらない。このための定数を積分定数といい、通常、\(C\)で表す。
積分公式
$$\int x^n dx = \frac{x^{n+1}}{n+1} + C \;\;\; (n \neq -1) \;\;\; \cdots (1) \\ \int e^x dx = e^x + C, \;\;\; \int \frac{1}{x} dx = \log x + C \;\;\; \cdots (2) \\ \int \cos x dx = \sin x + C ,\;\;\; \int \sin x dx = - \cos x + C \;\;\; \cdots (3)$$
微分と同様に、線形性は積分でも成立する。合成関数の微分公式に対応する積分規則は、置換積分法となる。すなわち、\(x = g(u)\)ならば、$$\int f(x) dx = \int \frac{d g(u)}{du} f\left(g(u)\right)du \;\;\; \cdots (4)$$となる。例として、\(x \lt 0\)のとき式(2)の右辺の\(log x\)が実数にならない。そこで、\(x=-x'\)と置換積分すると、$$\int \frac{1}{x}dx = \log |x| + C$$と拡張した公式にできる。
微分公式
・合成関数の微分$$\frac{d}{dx} f\left(g(x) \right) = \frac{d g(x)}{dx} \frac{d f \left(g(x)\right)}{dg(x)} $$
・関数の積の微分(ライプニッツ規則)
$$\frac{d}{dx} \left(f(x) g(x) \right) \\= \frac{df(x)}{dx} g(x) + f(x) \frac{d g(x)}{dx}$$
関数の積の微分に対応する積分規則は、部分積分法となる。つまり、$$\int \frac{d f(x)}{dx} g(x) dx = f(x)g(x) - \int f(x) \frac{d g(x)}{dx} dx \;\;\; \cdots (5)$$である。
※部分積分のように、積分計算は一般に難しく初等関数の積分でも初等関数で表せないことが多い。
リーマン積分
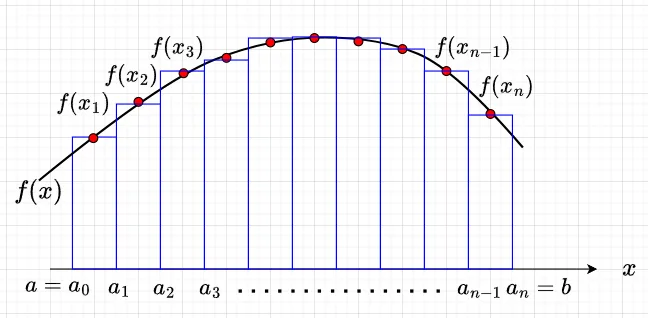
積分の定義として、関数のグラフをヒストグラムの極限と見た時の面積と考える。これをリーマン積分という。リーマン積分の定義は、図1を参照して以下となる。
\(f(x)\)を閉区間\([a,b]\)で定義された\(x\)の関数とする。\(a = a_0 \lt a_1 \lt a_2 \lt \cdots \lt a_n = b\)として、区間\([a,b]\)を\(n\)区間\([a_0,a_1], \; [a_1, a_2],\;\cdots , \;[a_{n-1},a_n]\)に細分する。各区間\([a_{k-1},a_k]\)内に任意に\(x_k\)を選ぶ。\(\max_k(a_k - a_{k-1}) \rightarrow 0\)になるように\(n \rightarrow \infty\)としたとき、もし和 $$\sum_{k=1}^{\infty} (a_k - a_{k-1}) f(x_k)\;\;\; \cdots (6)$$が、細分の仕方や\(x_k\)の選び方に無関係に一定の値に近づくならば、それを\(a\)から\(b\)までの定積分とよび、$$\int_a^b f(x)dx$$と表記する。
つまり、区間\([a,b]\)を無限の\(n\)区間に細分していき長方形の面積の和を求めると、結局、\(f(x)\)による曲線と\(x\) 軸の間の面積に近似されていくことになる。これを定積分とする。
定積分は、図1より明らかなように単純加法性が成り立つ。$$\int_a^b f(x)dx + \int_b^c f(x)dx = \int_a^c f(x) dx \;\;\; \cdots (7)$$ 式(7)より、$$\int_a^{x+ \Delta x} f(\tau) d\tau - \int_a^x f(\tau) d\tau = \int_x^{x+\Delta x} f(\tau) d\tau$$この両辺を\(\Delta x\)で割り、\(\Delta x \rightarrow 0\)とすると、式(6)と微分の定義より、$$\frac{d}{dx} \int_a^x f(\tau) d\tau = f(x)$$となる。
これが微積分学の基本定理である。これより、\(f(x)\)の原始関数を\(F(x)\)とすると、$$\int_a^x f(\tau) d\tau = F(x) - F(a) \;\;\; \cdots (8)$$となる。積分定数は、\(x=a\)のとき、左辺が\(0\)になるので、\(-F(a)\)である。式(8)より、定積分の計算は不定積分の計算に帰着されることがわかる。
高階積分
微分の場合、高階導関数というものがしばしば現れる。これに対して、関数 \(f\) を1つの独立変数 \(x\) について繰り返し積分することを高階積分と言い、次のように表記する。$$\int_{a_n}^x \cdots \int_{a_1}^x f(\tau) d\tau^n = \int_{a_n}^x \left( \cdots \left( \int_{a_2}^x \left( \int_{a_1}^x f(\tau)d\tau \right) d \tau \right) d \tau \right) d \tau$$ このような高階積分は、部分積分の公式(5)を使うことで、1階積分に帰着できる。例えば、2階積分は$$\int_a^x d \tau \int_a^\tau f(t) dt = \int_a^x \left[ \frac{d(\tau -a)}{d \tau} \int_a^\tau f(t) dt\right] \\ = (x-a)\int_a^x f(\tau)d\tau - \int_a^x (\tau -a)f(\tau) d\tau$$のように1階積分で書ける。これを繰り返すことで、\(n\)階積分は1階積分で書ける。

