7. 解析関数（微積分学）

2024年11月10日 2024年11月11日

tctyam

解析関数とは、ある点の近傍で無限回微分可能であり、かつその点におけるテイラー展開がその近傍で収束するような関数のことを指す。
複素変数$z$の関数$w = f(z)$が微分可能なとき、すなわち、$$\lim_{\Delta z \to 0} \frac{\Delta w}{\Delta z} = \lim_{\Delta z \to 0}\frac{f(z+\Delta z) -f(z)}{\Delta z}　\;\;\; \cdots (1)$$が存在するとき、$w=f(z)$は$z$において正則、または、解析的であるという。正則であれば何回でも微分可能で、テイラー展開も可能となる。
$\Delta z$は複素変数なので、2次元量である。このため、式(1)は無限に多くの方向から$0$に近づいたときの極限値が一致するという、極めて強い条件を要求している。このことを明確に示したのがコーシー・リーマンの微分方程式である。

※以下、虚数単位は$j$の表記を使う。

コーシー・リーマンの微分方程式

複素関数$f(z)$は複素数上で定義され、複素数の値を持つ関数である。$f(z)$の実部を$u$、虚部を$v$とする。つまり複素数$z = x + jy$を入力したときの出力を$$f(x+jy) = u(x,y) + jv(x,y)$$と書く。（$x,\;y$は実数、$u,\;v$は２変数実関数である。）この複素関数が正則であるための必要十分条件は、$$\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} , \;\;\; \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x}$$が成立することである。これは、$$\left(\frac{\partial}{\partial x } + j \frac{\partial}{\partial y} \right) (u + jv) = \left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) + j \left(\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \right) = 0$$とまとめられる。これが成立するには、虚部=0、実部=0が条件となる。これから、$x, \;y$の2変数の関数を2変数$z=x+jy,\; z^{*}=x-jy$の関数と見直した時、$z^{*}$に依存しないという条件、$$\frac{\partial w}{\partial z^{*}} = 0$$となっている。すなわち、$$dw = \frac{\partial w}{\partial z}dz + \frac{\partial w}{\partial z^{*}}dz^{*} = \frac{\partial w}{\partial z}dz$$であり、２変数に関する全微分の式が１変数の微分の式に帰着するということが、複素変数の意味での微分可能性である。

［例１］$f(z) = z^2$の微分可能性
$$f(x +jy) =(x + jy)^2 \\= (x^2 - y^2) + 2j xy$$より、$u = x^2 - y^2 ,\;\; v=2xy$である。このとき、$$\frac{\partial u}{\partial x } = 2x = \frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y} = -2y = -\frac{\partial v}{\partial x}$$とコーシー・リーマンの微分方程式が成立するので、微分可能である。

［例２］$g(z) = z^{*}$の微分可能性
$g(x + jy) = x-jy$より、$u= x,\;\; v =-y$である。このとき、$$\frac{\partial u}{\partial x} = 1 \\ \frac{\partial v}{\partial y} = -1$$となり、コーシー・リーマンの微分方程式が成立しないので、微分不可能である。

コーシー・リーマンの微分方程式の簡易証明

$\Delta z = \Delta x + j \Delta y$として考える。
・実軸方向での微分を考えると、$\Delta z = \Delta x$なので、$$\frac{df}{dz} = \lim_{\Delta x \to 0} \frac{u(x+ \Delta x, y ) + jv(x + \Delta x ,y) - [u(x,y) + j v(x,y)]}{\Delta x} \\=\lim_{ \Delta x \to 0} \frac{u(x+\Delta x,y)- u(x,y)}{\Delta x} + j \lim_{ \Delta x \to 0} \frac{v(x + \Delta x ,y) - v(x,y)}{\Delta x}$$ 従って、$$\frac{\partial f}{\partial z} = \frac{\partial u}{\partial x} + j \frac{\partial v}{\partial x}$$
・虚軸方向での微分を考えると、$\Delta z = j \Delta y$なので、$$\frac{df}{dz} = \lim_{\Delta y \to 0} \frac{u(x, y + \Delta y ) + jv(x ,y + \Delta y) - [u(x,y) + j v(x,y)]}{ j\Delta y} \\=\lim_{ \Delta y \to 0} \frac{u(x,y + \Delta y)- u(x,y)}{j \Delta y} + j \lim_{ \Delta y \to 0} \frac{v(x ,y + \Delta y) - v(x,y)}{j \Delta y}$$ 従って、$$\frac{\partial f}{\partial z} = \frac{1}{j} \left(\frac{\partial u}{\partial y} + j \frac{\partial v}{\partial y}\right) = \frac{\partial v}{\partial y} - j\frac{\partial u}{\partial y}$$ 複素導関数の存在には、実軸方向と虚軸方向からの微分が一致する必要がある。よって、それぞれの実部、虚部が等しいことが条件となり、これがコーシー・リーマンの微分方程式である。$$\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} , \;\;\; \frac{\partial u}{\partial y} = - \frac{\partial v}{\partial x}$$

コーシーの積分定理

複素変数の微分に関する操作や公式は実変数の場合と同じであるが、積分に関しては新たな事象が生ずる。それは変域が面の拡がりを持っているためで、両端点を決めるだけでは定積分が定義できないということである。つまり、複素平面上のどの道筋を辿るかも指定しなければならない。この積分の道筋を積分路という。

積分路$P$についての定積分は、$$\int_{P} f(z) dz$$と表記する。図１において、$\zeta_j$は曲線$P$上の$z_{j-1}$と$z_j$の間の点で、$\delta \equiv \max |z_j - z_{j-1}|$として、$$\int_P f(z) dz = \lim_{\delta \to 0} \sum_{j=1}^n f(\zeta_j)(z_j - z_{j-1})$$である。

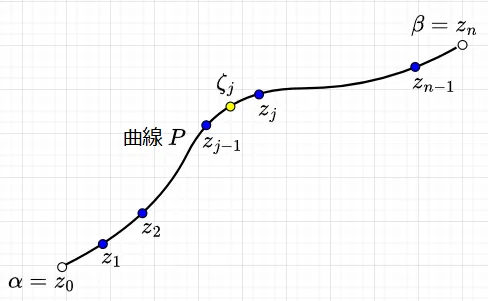
$f(z)$が正則であるような領域内では、両端点を固定すれば、積分路をどう変えても積分値は不変である。つまり、一意的に原始関数が存在する。これがコーシーの定理である。

コーシーの定理

領域$D$で定義された関数$f(z)$が、$D$内の単一閉曲線$C$で囲まれた部分で正則ならば、閉曲線に沿った一周積分は零である。つまり、$$\int_C f(z) dz = 0 \;\;\; \cdots (2)$$である。

図２のように、$C$上に2点$\alpha,\;\beta$をとり$C$を$\alpha$から$\beta$への積分路$P$と$\beta$から$\alpha$への積分路$P'$に分けたとすると、$$\int_P f(z) dz = -\int_{P'} f(z) dz = \int_{-P'} f(z) dz$$で、$-P'$は$P$とは異なる$\alpha$から$\beta$への積分路なので、積分路のとり方によらないことになる。

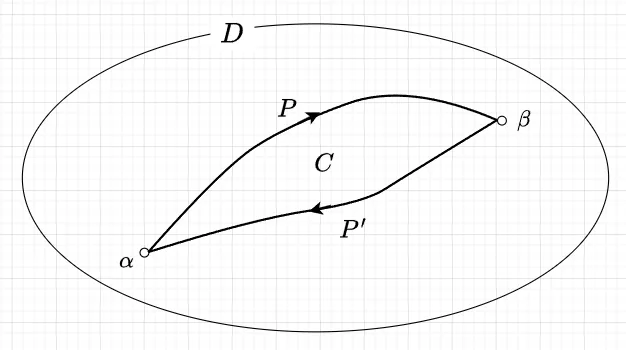
これは、$$\int_P f(z) dz +\int_{P'} f(z) dz = 0$$である。
さらに、$$\int_{\alpha}^{\beta} f(z) dz = F(\beta) - F(\alpha)$$と書ける。

コーシーの積分表示

複素平面上のある一点$z=a$における複素関数の値$f(a)$を、その点を囲む一周積分として表すのがコーシーの積分表示である。$C$で囲まれた領域に特異点（正則ではない点）が存在するとき、式(2)の左辺の積分は$0$になるとはいえなくなる。一点（特異点）を含む十分に小さい開いた領域をその点の近傍という。特異点がその点自身以外の近傍で正則な場合、孤立特異点という。既約有理関数の分母の零点は極と呼ばれ、最も簡単な孤立特異点である。

コーシーの積分公式

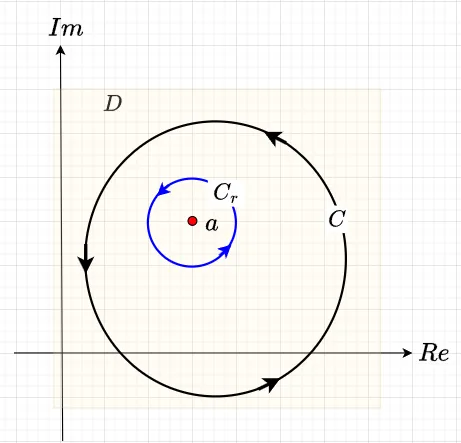
$f(z)$が$C$で囲まれた領域$D$で正則で、$z=a$が$D$内にあるとき、$$\frac{1}{2 \pi j}\int_C \frac{f(z)}{z-a} dz = f(a) \;\;\; \cdots (3)$$である。ただし、$C$は正の方向（反時計回り）に回るものとする。

コーシーの定理により、点$z =a$を正方向に回る半径$r \to 0$の円$C_r$に置き換えられる。よって、式(3)の左辺は$f(a) \lim_{r \to 0} I_r$に帰着される。ただし、$$I_r \equiv \frac{1}{2 \pi j}\int_{C_r(a)} \frac{1}{z-a} dz$$とする。これは、$z -a = re^{j \theta}$とおけば、$dz = jre^{j\theta} d \theta$なので、$$I_r = \frac{1}{2 \pi j} j \int_0^{2 \pi} d\theta =1$$である。よって、式(3)となる。

式(3)で、文字を書き換えて左辺、右辺を入れ換えると、$$f(z) = \frac{1}{2 \pi j}\int_C \frac{f(\zeta)}{\zeta - z}d \zeta \;\;\; \cdots(4)$$となる。すなわち、任意の正則関数が積分表示できることになる。これをコーシーの積分表示という。式(4)を$n$回微分すれば、$n$階導関数に関する積分表示が得られる。$$f^{(n)}(z) = \frac{n!}{2 \pi j} \int_C \frac{f(\zeta)}{(\zeta -z)^{n+1}} d \zeta$$ これは、何回でも微分可能であることを示している。

カテゴリー: 電気数学