9. ガンマ関数とベータ関数(微積分学)
ガンマ関数
ガンマ関数は、自然数に対して定義される階乗の概念を連続数に一般化した関数である。ガンマ関数は複素数の実部が正の領域において定義され、特に実数の範囲で広く利用される。
ガンマ関数の定義
ガンマ関数\( \Gamma(\nu)\) は、複素数\(\nu\) の実部が正のときに次の定積分で定義される。
$$\Gamma(\nu) = \int_0^{\infty} x^{\nu-1} e^{-x} dx \;\;\; \cdots (1)$$この積分は \(\nu \gt 0\)の実数や複素数において収束する。
式(1)で\(\nu\)を\(\nu + 1\)に置き換えて部分積分すると、\(Re\{\nu\} \gt 0\)なので式(2)に示す部分積分の右辺第1項は\(0\)となる。従って、$$\Gamma (\nu + 1) = \int_0^\infty x^{\nu} e^{-x} dx \\ = \nu \int_0^\infty x^{\nu -1} e^{-x} dx = \nu \Gamma (\nu)$$となる。
よって、漸化式$$\Gamma (\nu +1) = \nu \Gamma (\nu) \;\;\; \cdots (3)$$が得られる。また、\(\Gamma (1) = \int_0^\infty e^{-x} dx = 1\)なので、\(\nu\)が自然数\(n\)のとき式(3)より、$$\Gamma (n+1) = n(n-1)(n-2) \cdots 2 \cdot 1 \cdot \Gamma(1) = n!$$である。すなわち、ガンマ関数は、自然数の階乗の拡張となっている。
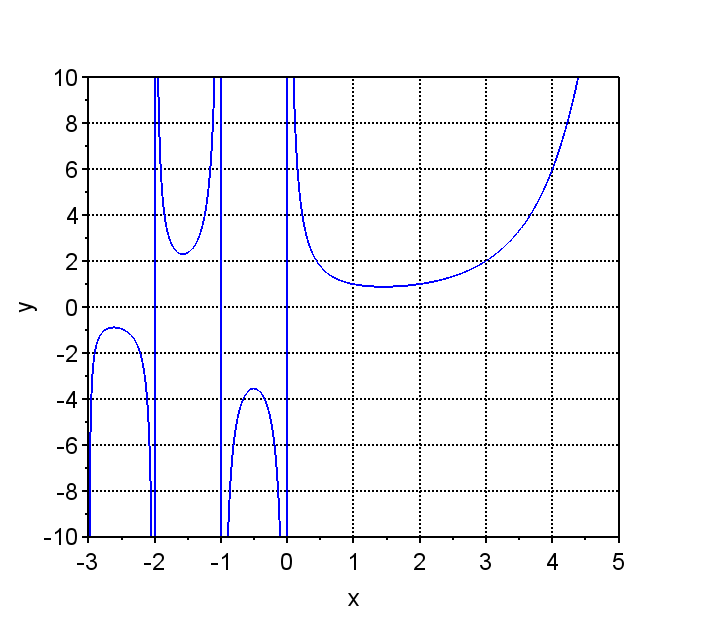
図1は、\(y = \Gamma(x)\)のグラフである。自然数の部分で、\(\Gamma (n+1) = n!\)が成立していることが分かる。
部分積分
$$\int \frac{df(x)}{dx} g(x) dx \\ = f(x)g(x) - \int f(x) \frac{dg(x)}{dx} dx \;\;\; \cdots (2)$$
\(\Gamma(\nu)\)を複素変数\(\nu\)の関数と見ると、式(1)は\(\nu\)について微分可能なので、\(Re\{\nu\} \gt 0\)において正則な関数である。従って、解析接続が考えられる。\(Re\{\nu\} \leq 0\)への解析接続は、式(3)から、$$\Gamma (\nu) = \frac{ \Gamma(\nu + n)}{\nu (\nu+1) (\nu+2) \cdots (\nu + n-1)}$$となるから、\(\Gamma (\nu)\)は、\(\nu = 0, -1,-2,\cdots\)で単純極をもち、それ以外では全複素平面上で正則である。
ベータ関数
式(1)において、変数変換\(x=t^2\)を行うと、\(dx = 2t dt\)なので、$$\Gamma (\nu) = 2 \int_0^\infty t^{2\nu -1} e^{-t^2} dt \;\;\; \cdots (4)$$となる。変数記号\(\nu ,\;t\)を\(\mu, \;s\)に変更すると、$$\Gamma (\mu) = 2 \int_0^\infty s^{2\mu -1} e^{-s^2} ds \;\;\; \cdots (5)$$と書ける。式(4)と式(5)の積は、$$\Gamma (\mu) \Gamma (\nu) = 4\int_0^\infty \int_0^\infty s^{2\mu -1} t^{2\nu -1} e^{-(s^2+t^2)} ds dt $$となる。この式の右辺は、\((s,\;t)\)平面の第1象限での積分なので、極座標\(s = r \cos \theta ,\;\; t = r \sin \theta\)に変数変換すると、積分範囲は、\(r : 0 \;\to \infty\)、\(\theta: \;0 \to \pi/2\)となり、\(dsdt = r d\theta dr\)(\(dsdt\)の微小面積が\(rd\theta dr\)と表せる)となる。従って、$$\Gamma(\mu) \Gamma(\nu) = 4 \int_0^{\pi/2} (\cos\theta)^{2\mu -1} (\sin \theta)^{2 \nu -1} d \theta \int_0^{\infty} r^{2\mu + 2\nu -1} e^{-r^2} dr$$ここで、$$\int_0^{\infty} r^{2\mu + 2\nu -1} e^{-r^2} dr$$の積分は、式(4)より、\(\frac{1}{2}\Gamma(\mu + \nu)\)である。また、$$\int_0^{\pi/2} (\cos\theta)^{2\mu -1} (\sin \theta)^{2 \nu -1} d \theta$$の積分は、\(\cos^2 \theta = x\)とおくと、\(\sin^2 \theta = 1 - x\)、\(-2\cos \theta \sin \theta d \theta = dx\)なので、$$\int_0^{\pi/2} (\cos\theta)^{2\mu -1} (\sin \theta)^{2 \nu -1} d \theta = \frac{1}{2} \int_0^1 x^{\mu -1} (1-x)^{\nu -1} dx \;\;\; \cdots (6)$$となる。
以上より、オイラーのベータ関数は定積分$$B(\mu, \;\nu) \equiv \int_0^1 x^{\mu -1} (1-x)^{\nu -1} dx \;\;\; \cdots (7)$$により定義される。この定義を使うと、$$B(\mu,\; \nu) = \frac{\Gamma(\mu) \Gamma(\nu)}{\Gamma(\mu + \nu)} \;\;\; \cdots (8)$$が得られる。
ここで、\(\mu = \nu = 1/2\)とおくと、式(6)の左辺より、$$\int_0^{\pi/2} (\cos\theta)^{0} (\sin \theta)^{0} d \theta = \int_0^{\pi/2} d \theta = \frac{\pi}{2}$$である。また、式(6)の右辺は、$$\frac{1}{2} \int_0^1 x^{\mu -1} (1-x)^{\nu -1} dx = \frac{1}{2} B(\mu, \; \nu)$$なので、式(8)より、$$\frac{\pi}{2} = \frac{1}{2} \cdot \frac{ [\Gamma(\frac{1}{2})]^2}{\Gamma(1)}$$となる。よって、$$\Gamma \left(\frac{1}{2} \right) = \sqrt{\pi} \;\;\; \cdots(9)$$が得られる。これと式(3)を組み合わせれば、順次、半奇数値のガンマ関数の値が求まる。
ガンマ関数の公式
式(6)において左辺と右辺を入れ換え、\(\mu = \nu\)として、三角関数の倍角公式を使うと、$$ \frac{1}{2} \int_0^1 [x(1-x)]^{\nu -1} dx = \int_0^{\pi/2} \left(\frac{\sin(2 \theta)}{2}\right)^{2\nu - 1} d\theta\;\;\; \cdots (10)$$となる。\(2 \theta = \phi\)と変数変換すると、\(d\theta = \frac{1}{2} d\phi\)であり、\(\theta : 0 \to \pi/2\)は、\(\phi : 0 \to \pi\)なので、$$ \int_0^{\pi/2} \left(\frac{\sin(2 \theta)}{2}\right)^{2\nu - 1} d \theta = 2^{-2\nu} \int_0^\pi (\sin \phi)^{2\nu -1} d\phi = 2^{-2\nu} \cdot 2 \int_0^{\pi/2} (\sin \phi)^{2\nu-1} d\phi $$となる。さらに、\(\mu =1/2\)として式(6)を使うと、 $$= 2^{-2 \nu +1} \cdot \frac{1}{2} \int_0^1 x^{-1/2} (1-x)^{\nu -1} \;\;\; \cdots (11)$$と表せる。式(10)の左辺と式(11)はベータ関数で表せるので、$$\frac{\left(\Gamma(\nu)\right)^2}{2 \Gamma(2 \nu)} = 2^{-2\nu} \frac{\Gamma(\frac{1}{2}) \Gamma(\nu)}{\Gamma(\nu + \frac{1}{2})}$$を得る。これに式(9)を代入すると、ガンマ関数の2倍公式$$\Gamma(\nu) \Gamma(\nu + \frac{1}{2}) = 2^{-2 \nu +1} \sqrt{\pi} \Gamma(2 \nu)$$が得られる。
・ガンマ関数の反射公式(オイラーの反射公式)
\(0 \lt Re\{\mu\} \lt 1\)と仮定して、式(8)において、\(\nu = 1 -\mu\)とすると、$$B(\mu,\; 1-\mu) = \frac{\Gamma(\mu) \Gamma(1 - \mu)}{\Gamma(\mu + 1 - \mu)} = \frac{\Gamma(\mu) \Gamma(1 - \mu)}{\Gamma(1)} = \Gamma(\mu) \Gamma(1 - \mu) $$となる。また、式(7)より、$$B(\mu,\; 1-\mu) = \int_0^1 x^{\mu -1} (1-x)^{1- \mu -1} dx = \int_0^1 x^{\mu -1} (1-x)^{- \mu} dx$$となる。よって、$$\Gamma(\mu) \Gamma(1 - \mu) = \int_0^1 x^{\mu -1} (1-x)^{- \mu} dx$$である。ここで、\(x=\frac{t}{1+t}\)と変数変換すると、\(x : 0 \to 1\)、\(t : 0 \to \infty\)であり、\(dx= \frac{1}{(1+t)^2} dt\)なので、$$\Gamma(\mu) \Gamma(1 - \mu) = \int_0^\infty \frac{t^{\mu-1}}{1+t}dt \equiv L(\mu) \;\;\; \cdots (12)$$となる。\(L(\mu)\)の定積分は、留数定理を利用した複素積分を経由して求める。
まず、\(L(\mu)\)の被積分関数を複素変数\(t\)の解析関数として複素積分を行う。
被積分関数は、極\(t=-1\)を除き正則である。図2に示すような積分路\(C\)を考える。原点\(0\)から実軸の正の上側に沿って\(R+j0\)に進み、そこから原点を中心とした半径\(R\)の円周上を正方向(反時計方向)に回って、\(R-j0\)に到る。そこから実軸の正の下側に沿って原点\(0\)に戻る。\(C\)に囲まれた領域の中での特異点(極)は\(t = -1\)で、これは\(t=\cos\pi+j\sin\pi = e^{j\pi}\)と表せる。従って、留数定理により、$$\int_C \frac{t^{\mu -1}}{1 + t} dt = 2\pi j e^{j \pi(\mu -1)} \;\;\; \cdots (13)$$となる。
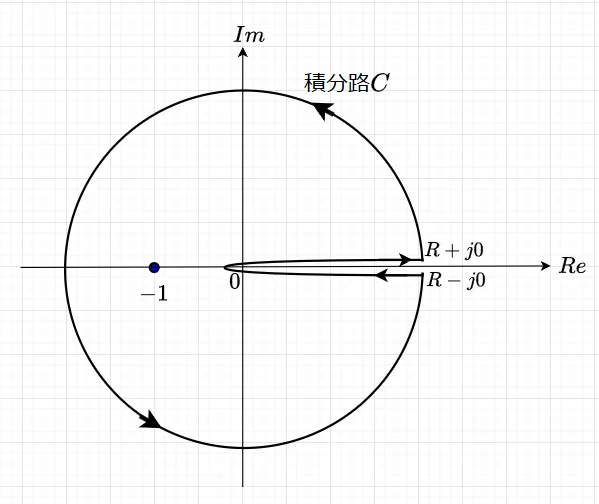
式(13)の左辺は、\(0 \lt Re\{\mu\} \lt 1\)の仮定より、\(Re\{\mu -1\} \lt 0\)なので、\(R \to \infty\)とすると、積分路\(C\)の円周からの寄与は\(0\)となる。残る積分は、実軸の上下を往復した部分の積分となる。実軸の原点から正方向\(R+j0\)への積分は実積分で、\(R-j0\)から原点への積分は向きが逆で偏角が\(2\pi\)進んでいるので、\((1 - e^{2 \pi j\mu})L(\mu)\)に等しい。よって、式(13)より、$$L(\mu)(1 - e^{2 \pi j \mu}) = 2 \pi j e^{j \pi(\mu -1)}$$である。これより、$$L(\mu) = \frac{2 \pi j e^{j \pi (\mu -1)}}{1 - e^{2 \pi j \mu}} =\frac{-2 \pi j e^{j \pi \mu}}{1 - e^{2 \pi j \mu}} = \frac{- 2 \pi j}{e^{-j \pi \mu} - e^{j \pi \mu}} \\= \frac{ \pi (2j)}{e^{j \pi \mu} - e^{-j \pi\mu}} = \frac{\pi}{\sin(\pi \mu)} \;\;\; \cdots (14)$$が求まる。よって、$$\Gamma(\mu) \Gamma(1 - \mu) = \frac{\pi}{\sin(\pi \mu)} $$でる。これをガンマ関数の反射公式という。
これを使うと、\(\mu=1/2\)として、$$\Gamma\left(\frac{1}{2}\right) \Gamma\left(\frac{1}{2}\right) = \frac{\pi}{\sin (\pi /2)} = \pi$$よって、$$\Gamma\left(\frac{1}{2}\right) = \sqrt{\pi}$$が求まる。これは、当然、式(9)の結果と同じである。


“9. ガンマ関数とベータ関数(微積分学)” に対して2件のコメントがあります。
コメントは受け付けていません。