7-1. 正規分布
正規分布は、統計学で最もよく知られ、利用されている連続的な確率分布の一つである。左右対称の釣鐘型のグラフで表される。自然界や社会現象において、多くのデータが正規分布に従う傾向があり、そのため統計学の様々な場面で活用される。
正規分布の特徴
正規分布は以下のような特徴を持つ。
・左右対称:平均値を軸にして左右対称な形をしている。
・平均値、中央値、最頻値の一致:これらの値はすべて同じ値になる。
・分散:データの散らばり具合を示す指標で、分散が大きいほど、グラフは平らになり、小さいほど尖った形になる。
・中心極限定理:多くの独立な確率変数の和は、サンプルサイズが大きくなるにつれて正規分布に近づくという定理。
正規分布の一般形は、平均 \(\mu\)、分散 \(\sigma^2\)の場合、次の確率密度関数で表される。$$f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}} \;\;\;\cdots (1)$$正規分布では、
・分布の中心は平均 \(\mu\)に位置する。
・分散 \(\sigma^2\) によって分布の幅が決まる。
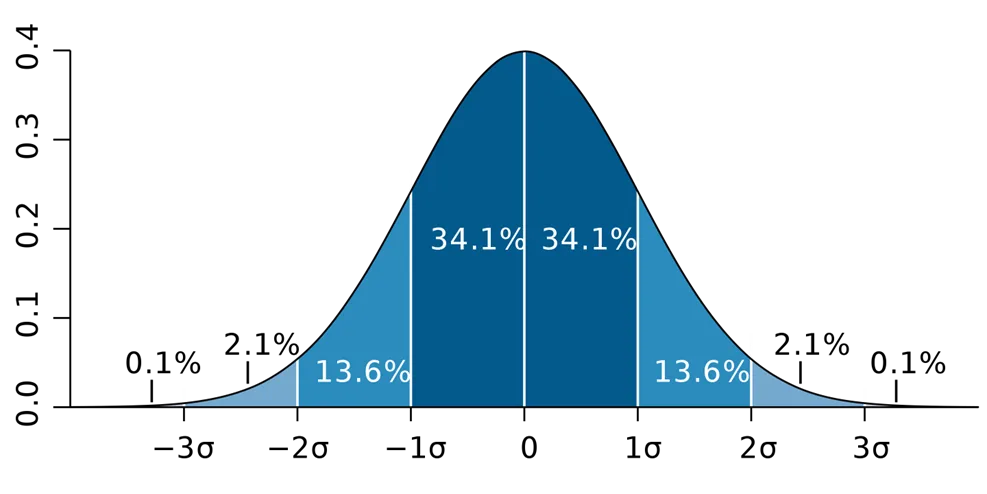
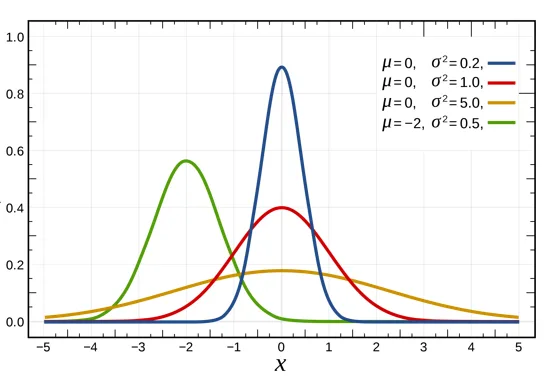
(\(\sigma^2, \;\mu\)による違い)
標準正規分布
標準正規分布は、式(1)において、平均 \(\mu = 0\)、分散 \(\sigma^2 = 1\)とした場合で、$$f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}\;\;\; \cdots(2)$$となる。
標準正規分布は、指数関数 \(e^{-\frac{x^2}{2}} \geq 0\)と分母 \(\sqrt{2\pi} \gt 0\) から、常に非負である。また、$$\int_{-\infty}^\infty f(x) dx = \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} dx = 1\;\;\;\cdots (3)$$なので、確率密度関数の要件を満たす。なお式(3)は、以下のようにガウス積分を利用して求める。
標準正規分布の密度関数では、指数の中が \(-\frac{x^2}{2}\) となっているため、変数変換を行う。$$u = \frac{x}{\sqrt{2}}, \quad du = \frac{1}{\sqrt{2}} dx$$積分範囲はそのまま \(-\infty\)から\(\infty\)。積分を次のように変形する。$$\int_{-\infty}^\infty e^{-\frac{x^2}{2}} dx = \sqrt{2} \int_{-\infty}^\infty e^{-u^2} du$$右辺にガウス積分の値を代入すると、$$\int_{-\infty}^\infty e^{-\frac{x^2}{2}} dx = \sqrt{2} \cdot \sqrt{\pi} = \sqrt{2\pi}$$となる。
密度関数 \(f(x)\)の前の係数 \(\frac{1}{\sqrt{2\pi}}\) を掛けると 1 になる。$$\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} dx = 1$$
ガウス積分
ガウス積分は、$$\int_{-\infty}^\infty e^{-x^2} dx = \sqrt{\pi}$$である。以下で導出できる。$$I = \left(\int_{-\infty}^\infty e^{-x^2} dx\right)^2 \\= \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-(x^2 + y^2)} dx dy$$極座標変換を行い、積分を計算する。 $$x^2 + y^2 = r^2, \quad dxdy = rdrd\theta$$範囲は$$r \in [0, \infty),\quad \theta \in [0, 2\pi]$$その結果、$$I = \int_0^{2\pi} d\theta \int_0^\infty e^{-r^2} r dr=\pi$$よって、 $$\int_{-\infty}^\infty e^{-x^2} dx = \sqrt{\pi}$$
正規分布の形状
ガウスは、観測誤差が「最もあり得る値(平均値)」を中心に対称的に分布し、遠ざかるほど発生頻度が低くなるという仮定を数学的に表現した。
基本的な仮定:
1.対称性:データは中心(平均値)を基準に左右対称に分布する。
2.漸減性:中心から離れるほど、データの頻度は指数的に減少する。
3.連続性:データは連続的に分布する。
4.確率密度の正規化:確率密度関数の積分値は 1 になる。
中心を 0 とする対称的な分布を仮定すると、確率密度関数 \(f(x)\) は次のように仮定される。$$f(x) = C e^{-kx^2}$$ここで、\(k > 0\) は分布の幅を調整する定数。\(C\) は正規化定数。
確率密度関数は次の正規化条件を満たさなければならない。$$\int_{-\infty}^\infty f(x) dx = 1$$これを適用すると$$\int_{-\infty}^\infty C e^{-kx^2} dx = 1$$である。ガウス積分$$\int_{-\infty}^\infty e^{-kx^2} dx = \sqrt{\frac{\pi}{k}}$$を用いると、$$C \sqrt{\frac{\pi}{k}} = 1 \quad \Rightarrow \quad C = \sqrt{\frac{k}{\pi}}$$従って、確率密度関数は次の形になる。$$f(x) = \sqrt{\frac{k}{\pi}} e^{-kx^2}$$ここで、正規分布の分散 \(\sigma^2\) は、次のように定義される。$$\sigma^2 = \int_{-\infty}^\infty x^2 f(x) dx$$ $$\int_{-\infty}^{\infty}x^2 e^{-kx^2}dx = 2 \int_0^\infty x^2 e^{-kx^2}dx $$ \(u=kx^2 ,\; du =2kxdx ,\; dx = \frac{1}{2\sqrt{ku}}du\)と変数変換すると、$$\int_0^\infty x^2 e^{-kx^2} dx = \frac{1}{k}\int_0^\infty u e^{-u}\frac{1}{2\sqrt{ku}}du = \frac{1}{2k\sqrt{k}}\int_0^\infty u^{\frac{1}{2}}e^{-u}du = \frac{1}{4k\sqrt{k}}\sqrt{\pi}$$となる。(※\(\int_0^\infty u^{\frac{1}{2}}e^{-u}du \)の積分には、ガンマ関数を使っている。詳細は、ガンマ関数とベータ関数(微積分学)を参照してください。)
以上より、$$\int_{-\infty}^{\infty}x^2 e^{-kx^2}dx = \frac{\sqrt{\pi}}{2k\sqrt{k}}$$となるので、$$\sigma^2 = \int_{-\infty}^{\infty} x^2 f(x) dx=\int_{-\infty}^{\infty} x^2 \sqrt{\frac{k}{\pi}}e^{-kx^2}dx = \sqrt{\frac{k}{\pi}}\int_{-\infty}^{\infty}x^2 e^{-kx^2}dx = \frac{1}{2k}$$従って、定数 \(k\) は\(k = \frac{1}{2\sigma^2}\)と表せる。
以上より、正規分布の確率密度関数は次の形になる。$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{x^2}{2\sigma^2}}$$
このように、正規分布の形状は、仮定(対称性、漸減性、正規化)を満たす関数から、指数関数型の形状として唯一自然に導かれたものであるといえる。


“7-1. 正規分布” に対して1件のコメントがあります。
コメントは受け付けていません。