21. 内積と外積(ベクトル解析)
内積と外積は、ベクトルに関する基本的な演算であり、それぞれ異なる性質や用途を持っている。それぞれの定義、計算方法、幾何学的意味、応用について考える。
内積
図1に示すように、三次元の空間にあるベクトルを空間ベクトルという。ここで、ベクトルを解析的に表示するため、\(X\)方向で単位長さのベクトル(単位ベクトル)を\(i\)、\(Y\)方向の単位ベクトルを\(j\)、\(Z\)方向の単位ベクトルを\(k\)と表す。図1のベクトル\(A\)の\(X,Y,Z\)方向の成分を\(A_x,A_y,A_z\)とすると、$$A = A_x i + A_y j + A_z k$$となる。ベクトル\(A\)の絶対値(長さ)は、$$|A| = \sqrt{A_x^2 + A_y^2 + A_z^2} \;\;\; \cdots (1)$$である。
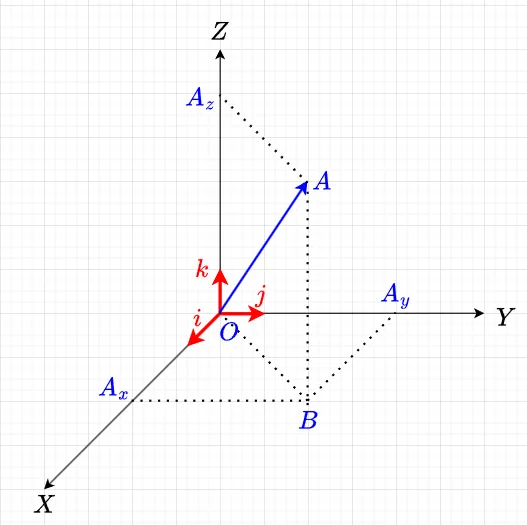
ベクトル\(B\)を\(B=B_x i + B_y j + B_z k\)とすると、ベクトル\(A\)とベクトル\(B\)の和と差は、$$A\pm B =(A_x \pm B_x)i + (A_y \pm B_y)j + (A_z \pm B_z)k \;\;\; \cdots(2)$$となる。
定数\(a\)との積は、$$Aa = aA =a( A_x i + A_y j + A_z k) = aA_x i + aA_y j + aA_zk \;\;\;\cdots(3)$$である。積として、まず内積を定義する。内積は、2つのベクトルの「スカラー量」を得る演算である。同一方向の成分の間の積だけ残るので、$$A\cdot B = (A_x i + A_y j + A_z k)\cdot(B_x i + B_y j + B_z k) \\= A_x B_x + A_y B_y + A_z B_z =|A||B|\cos \theta \;\;\; \cdots(4)$$である。\(\theta\)は、\(A\)と\(B\)の間の角である。式(4)でわかるように結果はスカラーとなるので、スカラー積ともいう。式(4)からわかるように$$A\cdot B = B\cdot A,\quad A\cdot A = A^2=|A|^2$$さらに、$$(A+B)\cdot C = A\cdot C + B \cdot C$$が成り立つ。
また、内積は、ベクトル同士の「方向の一致度」を表す。
・\(\cos\theta < 0\):ベクトルが鈍角を成している(反対方向に近い)。
・\(\cos\theta > 0\):ベクトルが鋭角を成している(同じ方向に近い)。
・\(\cos\theta = 0\):ベクトルが直交している。
外積
外積は、2つのベクトルの「新しいベクトル」を得る演算である。外積の結果はベクトルであり、平面に垂直な方向を示す。結果がベクトルになるので、ベクトル積ともいう。
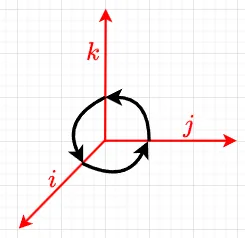
図2に示すように、右手系の単位ベクトルを\(i,j,k\)とすると、\(i \times j\)は、\(i\)から\(j\)の方向に右ネジを回転すると、\(k\)の方向に進むので、\(i \times j=k\)となり、\(j \times i \)は、\(-k\)となる。まとめると、$$j\times k =i,\quad k \times i =j, \quad i \times j =k \\ j \times i = -k, \quad k \times j =-i,\quad i \times k = -j \\ i \times i = j \times j = k \times k =0 \;\;\; \cdots(5)$$となる。
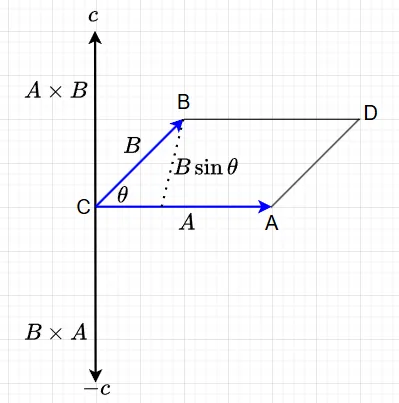
図3に示すように\(A \times B\)は、\(A\)と\(B\)を含む平面に垂直で\(A\)から\(B\)に右ネジを回して、その進行方向が\(A \times B\)の方向となり、その大きさは\(|A||B|\sin\theta\)となる。\(B \times A\)は、大きさは等しいが\(B\)から\(A\)の方向の回転なので、方向は\(A \times B\)と反対になる。\(c\)を\(A \times B\)方向の単位ベクトルとすると$$A \times B = - B \times A = c |A||B|\sin \theta$$となる。
$$A = A_x i + A_y j + A_z k ,\quad B=B_x i + B_y j + B_z k$$とおくと、式(5)の関係を使って、$$A \times B = i(A_y B_z - A_x B_y) + j(A_z B_x - A_x B_z) + k(A_x B_y - A_y B_x)$$となる。これを行列式を使って表すと$$A \times B = \begin{vmatrix} i & j & k\\ A_x & A_y & A_z \\ B_x & B_y & B_z \end{vmatrix}$$ また、ベクトルの外積にも分配則が成立する。$$A \times (B + C) = A \times B + A \times C$$
三つのベクトルの積
3つのベクトルに対して、内積と外積を組み合わせる操作には、いくつかの重要な演算がある。これらは、ベクトルの幾何学的性質や空間的な関係を理解するために使用される。
内積とベクトルの積
\(A(BC)\)あるいは\(AB\cdot C\)の場合、\(BC\) はスカラーとなるので、\(A(BC)\)は、ベクトル\(A\)のスカラー倍となる。また、\((AB)C\)の場合は、\(AB\)はスカラーとなるので、ベクトル\(C\)のスカラー倍となる。従って、$$A(BC) \neq (AB)C$$である。
スカラー三重積
スカラー三重積は、外積と内積を組み合わせた操作、
$$A \cdot (B \times C)$$である。これは、\(B \times C\)を計算して新しいベクトルを得て、そのベクトルと \(A\)の内積を計算することになる。従って、結果はスカラーとなる。
幾何学的意味としては、以下となる。
・スカラー三重積は、\(A,B,C\) が張る平行六面体の体積を表す。
・絶対値が体積を表し、符号は\(A,B,C\)の順序が右手系かどうかを示す。
性質として、$$A \cdot (B \times C) = B \cdot (C \times A) = C \cdot (A \times B)$$(成分の循環移動による値の不変性)があり、また、スカラー三重積が 0 のとき、3つのベクトルは同一平面上にある。
ベクトル三重積
ベクトル三重積は、2回の外積を組み合わせた操作で、$$A \times (B \times C)$$である。ベクトル\(A\)とベクトル\(B \times C\)の外積であるから、結果はベクトルである。
\(B \times C = D\)と置くと$$A \times D = \begin{vmatrix} i & j & k\\ A_x & A_y & A_z \\ D_x & D_y & D_z \end{vmatrix} \\ D = B \times C = \begin{vmatrix} i & j & k\\ B_x & B_y & B_z \\ C_x & C_y & C_z \end{vmatrix}$$なので、\(x\)成分については、$$[A \times (B \times C)]_x = A_y(B_x C_y - B_yC_x) - A_z(B_z C_x - B_x C_z) + A_xB_xC_x - A_xB_xC_x \\ = B_x(A_x C_x + A_y C_y + A_z C_z) - C_x(A_x B_x + A_y B_y + A_z B_z) \\=B_x(AC) - C_x(AB)$$となる。同様にして、$$[A \times (B \times C)]_y = B_y(AC) - C_y(AB) \\ [A \times (B \times C)]_z = B_z(AC) - C_z(AB)$$となるので、これら成分をまとめると$$A \times(B \times C) = B(AC) - C(AB)$$ となる。また、$$(A \times B) \times C = B(AC) - A(BC)$$である。
よって、ベクトル三重積は交換法則を満たさない。$$A \times (B \times C) \neq (A \times B) \times C$$


“21. 内積と外積(ベクトル解析)” に対して2件のコメントがあります。
コメントは受け付けていません。