22. ベクトルの微分積分(ベクトル解析)
ベクトルの微分と積分は、ベクトル解析や物理学、工学において重要な数学的ツールである。これらは、スカラー場やベクトル場における変化の解析や物理現象の記述に広く使われる。
ベクトルの微分
ベクトルの微分は、スカラー関数の微分を拡張した概念で、ベクトルの各成分について微分を行う。
ベクトル\(A\)がスカラー量である時間\(t\)の関数のとき、\(A\)の3成分\(A_x,A_y,A_z\)も\(t\)の関数であり、\(A_x(t)\)はスカラー量であるから、$$\frac{d A_x}{dt} = \lim_{\Delta t \to 0}\frac{A_x(t+\Delta t) - A_x(t)}{\Delta t}$$が\(x\)方向の微係数となる。同様に\(y,\;z\)方向も定義できるので、$$\frac{d A}{dt} = \frac{d A_x}{dt}i + \frac{d A_y}{dt}j + \frac{d A_z}{dt}k$$となる。
これと同様に推論していくと、$$\frac{d}{dt}(A+B) = \frac{dA}{dt} + \frac{dB}{dt} \\ \frac{d}{dt}(aA) = a\frac{dA}{dt} + A \frac{da}{dt} \\ \frac{d}{dt}(AB) = A\frac{dB}{dt} + B \frac{dA}{dt} \\ \frac{d}{dt}(A \times B) = \frac{dA}{dt} \times B + A \times \frac{dB}{dt}$$となる。
ベクトルの積分
ベクトルの積分は、スカラー関数の積分をベクトル空間に拡張した概念である。スカラー関数の積分が面積や体積を求めることに対応するように、ベクトルの積分は、ベクトル場における様々な物理的な量や概念を表すために用いられる。
線積分
曲線に沿ってベクトル場を積分することを線積分という。例として以下がある。
・仕事:力が物体をある経路に沿って移動させたときにする仕事は、力のベクトル場と変位のベクトルの線積分で表される。
・電位:静電場における電位は、電場の線積分によって定義される。
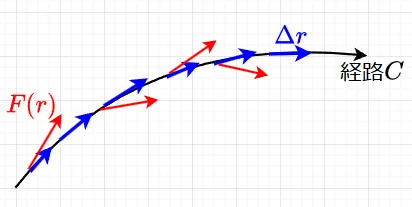
曲線 \(C\) 上で定義されたベクトル関数 \(F(r)\) の線積分は、式(1)で表される。$$\int_C F(r)\cdot dr \;\;\; \cdots (1)$$ ここで、\(dr\)は曲線 \(C\) 上の微小な線素ベクトルで、経路を近似するようなベクトルである。\(\cdot\)は内積を表す。\(dr\)は、$$dr = \begin{pmatrix} dx \\ dy \\dz\end{pmatrix}$$で定義される。
この積分は、曲線\(C\) に沿ってベクトル関数\(F(r)\)に接する成分の総和を表すことになる。従って、線積分を和の記号を使って書くと$$\int_C F(r) \cdot dr =\lim_{\Delta r_i \to 0}\sum_{i=1}^\infty F(r_i)\cdot \Delta r_i \;\;\; \cdots (2)$$である。\(\Delta r_i\)は、経路\(C\)を細かく分割してベクトルで表したもの(線素ベクトル)である。
面積分
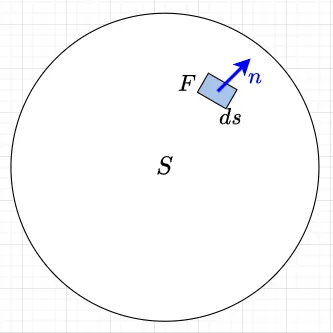
曲面 \(S\)上で定義されたベクトル場\(F(x,y,z)\)の面積分は、式(3)で表される。$$\iint_S F\cdot n ds \;\;\;\cdots (3)$$ここで、\(ds\)は曲面\(S\)上の微小な面積、\(n\)は曲面\(S\)上の単位法線ベクトル、\(\cdot\)は内積を表す。この積分は、曲面\(S\) を貫くベクトル場\(F\)の成分の総和を表している。(図2参照)
面積分の具体的な計算方法(パラメータ表示を用いた表現)
曲面\(S\)がパラメータ\( (u,v)\)によって次のように表されるとする。$$r(u, v) = (x(u, v), y(u, v), z(u, v)), \quad (u, v) \in D$$ここで\(D\)はパラメータ空間の定義域。
曲面上の小さな面積要素のベクトルは、次のように求められる。$$r_u = \frac{\partial r}{\partial u}, \quad r_v = \frac{\partial r}{\partial v}$$面積要素ベクトルは外積で計算される。$$r_u \times r_v$$面積要素の大きさ \(dS\)は$$dS = |r_u \times r_v| \, dudv$$となる。ベクトル場と面積要素の積分は$$\iint_S F \cdot n \, dS = \iint_D F \cdot \frac{r_u \times r_v}{|r_u \times r_v|} |r_u \times r_v| \, dudv$$で表せる。よって、$$\iint_S F \cdot n \, dS = \iint_D F \cdot (r_u \times r_v) \, dudv$$となる。
スカラーの勾配
例えば、空間にスカラー量である電荷が分布しているとき、電荷のスカラーは空間に分布していることになる。このようなスカラーが分布している区域をスカラー場といい、スカラー量はその点関数\(\varphi(x,y,z)\)として与えられる。電荷によって各点には電界が存在する。電界はベクトルなので、電界のベクトル場となる。
スカラー\(\varphi(x,y,z)\)は、通常、各点で大きさが異なるので、大きさが異なる場合にはある方向での\(varphi\)の大きさの変化は、大きさと方向があるのでベクトルとなる。\(\varphi(x,y,z)\)を\(x,y,z\)方向で偏微分すると、\(x,y,z\)方向の勾配は、$$\frac{\partial \varphi}{\partial x} ,\quad \frac{\partial \varphi}{\partial y} ,\quad \frac{\partial \varphi}{\partial z} $$となる。よって、\((x,y,z)\)の点の勾配はまとめて、式(4)となる。$$ \text{grad} \varphi = \nabla \varphi = \frac{\partial \varphi}{\partial x} i +\frac{\partial \varphi}{\partial y} j + \frac{\partial \varphi}{\partial z} k \\ \nabla = i \frac{\partial}{\partial x} + j\frac{\partial}{\partial y} + k \frac{\partial}{\partial z} \\ \nabla \varphi =i\frac{\partial \varphi}{\partial x} +j \frac{\partial \varphi}{\partial y} j + k \frac{\partial \varphi}{\partial z} \;\;\; \cdots (4)$$ここで、\(\nabla\)は方向を持っている微分演算子でナブラと読む。\(\nabla \varphi\)は、ベクトル\(\nabla\)とスカラー\(\varphi\)の積と見ることができ、\(\text{grad}\)はグラジエントの略で勾配を意味する。
スカラーを電位\(V\)にとると、電位の高い所から低いほうへの電荷を押しやる力、つまり電界\(E\)が生じるので、$$E = - \nabla V = - \text{grad} V$$となり、\(V\)は電界\(E\)のポテンシャル(電位)となる。
ベクトルの発散
ベクトルの発散とは、ある点からベクトルがどれくらい「湧き出ているか」または「吸い込まれているか」を表すスカラー場のことである。イメージとしては、水道の蛇口から水が勢いよく出ている様子が相当する。ベクトル場の各点における「拡がり」や「収縮」の度合いを表す量とも言える。
3次元空間におけるベクトル場 \(A = (A_x, A_y, A_z)\) の発散\(\text{div}A\) は、式(5)で表される。$$\text{div} A = \nabla \cdot A = (i \frac{\partial}{\partial x} + j\frac{\partial}{\partial y} + k \frac{\partial}{\partial z}) \cdot (A_x i + A_y j + A_z k) \\ = \frac{A_x}{\partial x} + \frac{A_y}{\partial y} +\frac{A_z}{\partial z} \;\;\; \cdots (5)$$
・発散が正: その点からベクトルが外に向かって湧き出ている。
・発散が負:その点に向かってベクトルが収束している。
・ 発散が0:その点におけるベクトルの湧き出しも吸い込みもない。
ということになる。
ガウスの発散定理
ガウスの発散定理は、ベクトル解析における基本的な定理であり、3次元空間で定義されたベクトル場の性質を結びつける重要な関係式である。
ガウスの発散定理は式(6)で表される。$$\iiint_V (\nabla \cdot F) \, dv = \iint_S F \cdot n \, ds \;\;\; \cdots (6)$$ここで、\(ds\):面積要素、\(F\):3次元空間で定義されたベクトル場、\(V\):体積(領域)、\(S\):\(V\) の境界面(閉曲面)、\(\nabla \cdot F\):ベクトル場の発散、\(n\):境界面の外向き単位法線ベクトル、\(dv\):体積要素 である。
式(6)の左辺は、領域\(V\) 内でのベクトル場の発散 \(\nabla \cdot F\)を体積全体にわたって積分する。発散は、ベクトル場がその点でどれだけ「発生」または「消失」しているかを示す。
式(6)の右辺は、領域\(V\)の境界面\(S\)を通過するベクトル場の流束(フラックス)を計算する。流速は、ベクトル場が境界をどれだけ通過するか(外向き方向)を表す。
ガウスの発散定理は、発散(局所的な変化率)を体積内で積分すると、そのベクトル場が境界面を通してどれだけ外へ流出するかに等しいことを意味する。
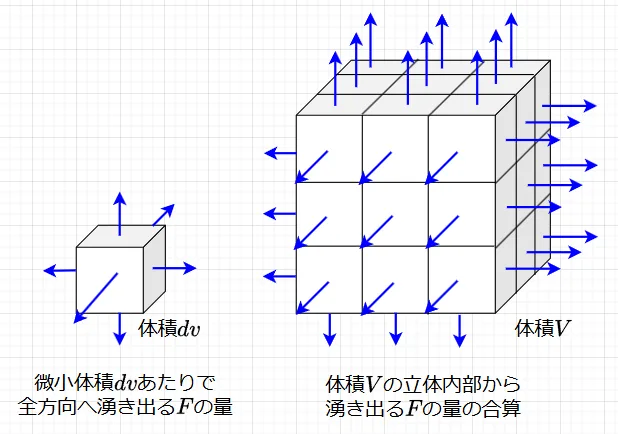
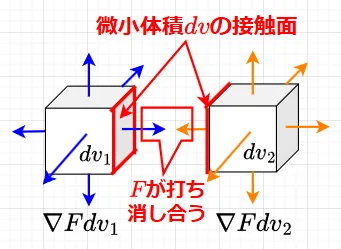
図3は、式(6)の左辺のイメージである。\(\nabla \cdot F\)がベクトル\(F\)の発散で、単位体積あたりで全方向へ湧き出る\(F\)の量を表し、\(\nabla \cdot F dv\)が微小体積\(dv\)あたりで全方向へ湧き出る\(F\)の量を表す。これを体積\(V\)の領域全体で積分したものが、式(6)の左辺である。体積\(V\)は、微小体積\(dv\)の足し合わせでできてる。このため、図4に示すように微小体積\(dv_1\)から湧き出る\(F\)の量(\(\nabla F \cdot dv_1\))と隣り合っている微小体積\(dv_2\)から湧き出る\(F\)の量(\(\nabla F \cdot dv_2\))は接触面において向きが反対になるため、打ち消し合う。これが接触している全ての面で起こる。従って、結局のところ、立体の表面からのみ\(F\)が湧き出ているということになる。これが式(6)の右辺である。\(F \cdot n\)は、微小面積\(ds\)を通る\(F\)の垂直方向(法線方向)の量のことを意味している。従って、表面積\(S\)の立体表面を通って外に出ていく\(F\)の量は、微小面積\(ds\)を通る\(F\)の垂直方向(法線方向)の量(\(F\cdot ds\))を足し合わせる、つまり面積分をすることで求めることができる。
ベクトルの回転
ベクトルの発散は微分演算子\(\nabla\)とベクトル\(F\)の内積であるが、\(\nabla\)と\(F\)の外積を\(F\)の回転、ローテーションという。$$\text{rot} F = \nabla \times F \\ \text{rot} F = \left(i \frac{\partial}{\partial x} + j \frac{\partial}{\partial y} + k \frac{\partial}{\partial z} \right) \times \left(F_x i + F_y j + F_z k\right) \\ = i\left(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\right) + j \left(\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}\right) + k \left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\right) \\ = \begin{vmatrix} i & j & k \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_x & F_y & F_z \end{vmatrix} \;\;\; \cdots (7)$$ \(\nabla\)がベクトルで\(F\)もベクトルなので、\(\nabla \times F\)はベクトルとなる。
回転 \(\nabla \times F\)は、ベクトル場\(F\)の周りに発生する局所的な回転の強さと方向を表す。
回転の大きさは、その点でのベクトル場が「どれだけ回転しているか」を表す。具体的には、ある小さな閉曲線を囲む面積あたりの循環量である。また、回転ベクトル \(\nabla \times F\)の方向は、右手の親指が示す方向(右ねじの法則)である。また、ベクトル場がある点で回転している「軸」を示す。
ベクトル\(F\)がベクトル\(P\)の回転で生じるとき、$$F = \nabla \times P$$ \(P\)を\(A\)のベクトル・ポテンシャルという。\(\varphi\)をスカラーとするとき、$$\text{rot}\cdot\text{grad} \varphi = \nabla \times \nabla \varphi = 0$$となる。
ベクトル演算の公式
\(\varphi,\;\psi\)をスカラー、\(A,\;B\)をベクトルとするとき、以下の公式が成立する。
$$\text{grad}\,(\varphi \psi) = \nabla(\varphi \psi) = \varphi \nabla \psi + \psi \nabla \varphi $$ $$ \text{div}\,(\varphi A) = \nabla (\varphi A) = \nabla \varphi \cdot A + \varphi \nabla A = \nabla \varphi \cdot A + \varphi \text{div}\, A $$ $$ \text{rot}\,(\varphi A) = \nabla \times (\varphi A) = \nabla \varphi \times A + \varphi \nabla \times A = \nabla \varphi \times A + \varphi \text{rot}\, A $$ $$ \text{div}\,(A \times B) = \nabla(A \times B) = B(\nabla \times A) - A(\nabla \times B) = B\text{rot}\, A - A \text{rot}\, B \\ \text{rot}\,(A \times B) = \nabla \times(A \times B) = (B \nabla)A - (A \nabla)B + A \text{div} \,B - B \text{div}\, A $$ $$ \text{grad}\,(AB) = \nabla(AB) = (A \nabla)B + (B\nabla)A + A\times \text{rot}\,B + B\times \text{rot}\, A$$
ベクトルの積分に関する定理
ストークスの定理
ストークスの定理は、曲面\(S\)上の回転の面積積分と、その曲面の境界 \(C\)に沿った線積分を結びつけるもので、ベクトル場の回転に関する微分積分の関係を表し、境界を通る循環(線積分)と、曲面全体での回転(面積積分)が等しいことを示している。ストークスの定理は式(8)で表される。$$\iint_S (\nabla \times F) \cdot n \, ds = \oint_C F \cdot dr \;\;\; \cdots (8)$$ここで、\(F\):ベクトル場、\(S\):滑らかな曲面(開曲面)、\(C = \partial S\):曲面 \(S\)の境界(閉曲線)、\(n\):曲面 \(S\)の単位法線ベクトル、\(ds\):曲面の微小面積要素、\(dr\):境界\(C\)上の微小ベクトル(線分要素)である。
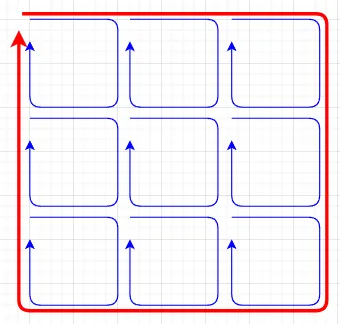
式(8)の左辺は面積積分で、\((\nabla \times F)\cdot n\)は、曲面上の点でのベクトル場の回転の法線成分を表す。面積積分 $$\iint_S (\nabla \times F) \cdot n \, ds$$は、曲面全体にわたる回転の「合計」を求める。
式(8)の右辺は線積分で、線積分 $$\oint_C F \cdot dr$$は、曲面の境界\(C\)に沿ったベクトル場の循環を求める。
ストークスの定理は、曲面内部の回転の合計(左辺)が、その境界に沿ったベクトル場の循環(右辺)と等しいことを示している。これは、ある領域におけるベクトルの渦の総和は、外縁に沿ったベクトルの和に等しい、ということで、図5に示すように、小さい渦が集まると、大きな渦になるということを意味している。
ガウスの線束定理
ベクトル場\(E\)(ここでは電場について考える)について、閉曲面 \(S\)を通過するフラックスは、その閉曲面\(S\)が囲む領域内のソースの総量に比例するという法則で、式(9)で表せる。$$\iint_S E \cdot n \, ds = \frac{Q}{\epsilon_0} \;\;\; \cdots (9)$$ここで、\(E\):電場ベクトル(電場強度)、\(S\):閉曲面(ガウス面)、\(n\):面の外向き単位法線ベクトル、\(ds\):微小面積要素、\(Q\):閉曲面内に存在する総電荷、\(\epsilon_0\):真空の誘電率、である。
式(9)の左辺の\(E \cdot n\)は電場が面の法線方向にどれだけ流れ出ているかを表す。流束(フラックス)$$ \iint_S E \cdot n \, ds$$は、電場が閉曲面を通過する総量である。式(9)の右辺は、電場を発生させるソース(電荷)\(Q\) の量が流束に比例することを示しており、また、電場は、正の電荷の場合は外向き、負の電荷の場合は内向きに働く。
式(10)のように、ガウスの線束定理を微分形式で表すと、電場の発散に関する式となる。$$\nabla \cdot E = \frac{\rho}{\epsilon_0} \;\;\; \cdots (10)$$ここで、\(\rho\):体積電荷密度(単位体積あたりの電荷量)、\(\nabla \cdot E\):電場の発散(電場がその点でどれだけ発生または収束しているか)である。

