1. \(H_{\infty}\)制御の概要
フィードバック制御と目的
図1はフィードバック制御系の基本構成図である。予定する基準動作を目標値\(r\)、実際の動作結果を制御量\(z_0\)、両者の差を偏差\(e\)といい、制御器\(C\)はこの偏差\(e\)の情報を使って制御用の信号である操作量(制御入力)\(u\)を生成する。
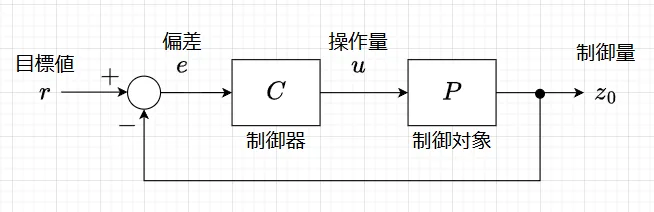
フィードバック制御系の基本的な設計仕様は、以下である。
・閉ループ系の安定
・定常時の偏差である定常偏差が0である
・過渡応答特性が良い
この仕様を満足する制御器\(K\)を制御対象の数学モデル\(P\)をもとに制御理論に基づいて設計する。しかし、通常、数学モデル\(P\)はなんらかの近似により与えられるため、実際の制御対象に対してモデル化誤差を持つ。従って、上記の設計仕様に加えて以下が要求される。
1)モデル化誤差があっても制御系が安定
2)モデル化誤差があっても定常偏差が0に保たれる
3)モデル化誤差があっても過渡応答特性が劣化しない
1)が満たされる場合、制御系はロバスト安定、2)が満たされる場合、定常ロバスト、1)、2)とも満たされる場合ロバストサーボ系と呼ぶ。3)はロバスト制御性能として扱う。
※古典制御理論(基礎制御工学 参照)では、周波数応答法を中心に試行錯誤や経験則により、このロバスト性を実現していたといえる。ただし、基本的に1入力1出力システムを対象として扱っていた。これに対して現代制御理論(システム制御 参照)では、状態方程式を基にして多入力多出力システムを統一的に扱い、状態フィードバック、最適レギュレータ、オブザーバの研究が発展した。しかし、ロバスト性に関する事項への対応は不十分であった。
\(H_{\infty}\)制御と評価関数
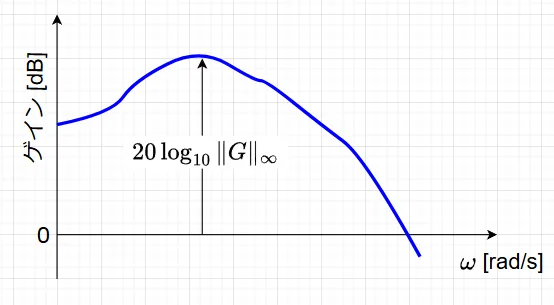
\(H_{\infty}\)制御を端的にいうとフィードバック制御によって適当な入力点から適当な出力点までの伝達関数の大きさをある値以下にする制御である。伝達関数の大きさの評価には周波数応答の絶対最大値を使う。具体的には図2のようにボード線図のゲインの絶対最大値(ベクトル線図だと原点からの距離の最大値)を式(1)のように書き\(H_\infty\)ノルムという。$$\|G(s)\|_\infty = \sup_{0 \leq \omega \leq \infty} | G(j\omega)| \;\;\; \cdots (1)$$
\(G(s)\)がベクトルや行列の場合の\(H_\infty\)ノルムは式(2)で定義する。$$\|G(s)\| = \sup_{0 \leq \omega \leq \infty}\bar{\sigma}\{G(j \omega)\} \;\;\; \cdots (2)$$ここで、\(\bar{\sigma}\)は行列の最大特異値で、一般に式(3)となる。$$\bar{\sigma}\{A\} = \left(\lambda_{\max}(A^{*} A)\right)^{1/2} \;\;\; \cdots (3)$$ここで、\(A^{*}=\bar{A}^T\)は複素行列の共役転置で、\(\lambda_{\max}\)は最大固有値である。
安定な伝達関数\(G(s)\)の2乗可積分な入力信号\(w\)と出力信号\(z\)のエネルギーとして、式(4),(5)を定義する。$$\|w\|_2 = \left\{ \int_0^\infty w^T(t)w(t) dt \right\}^{1/2} \;\;\; \cdots (4)$$ $$\|z\|_2 = \left\{ \int_0^\infty z^T(t)z(t) dt \right\}^{1/2} \;\;\; \cdots (5)$$このとき、\(H_\infty\)ノルムは式(6)となる。$$\|G(s)\|_\infty = \sup_w \frac{\|z\|_2}
{\|w\|_2} \;\;\;\cdots (6)$$ つまり、\(H_\infty\)ノルムは入出力のエネルギー比の最大値を意味している。
最大特異値、\(H_\infty\)に関する公式
$$\bar{\sigma} \{A\} \geq 0 \\ \bar{\sigma} \{A\} = 0 \leftrightarrow A= 0 \\ \bar{\sigma} \{\alpha A\} = |\alpha| \bar{\sigma} \{A\} \\ \bar{\sigma}\{A+B\} \leq \bar{\sigma}\{A\} + \bar{\sigma} \{B\} \\ \bar{\sigma} \{AB\} \leq \bar{\sigma} \{A\} \cdot \bar{\sigma} \{B\}$$ $$\|G\|_\infty \geq 0 \\ \|G\|_\infty = 0 \leftrightarrow G = 0 \\ \| \alpha G \|_\infty = |\alpha| \|G\|_\infty \\ \|G + H\|_\infty \leq \|G\|_\infty + \|H\|_\infty \\ \|G H \|_\infty \leq \|G\|_\infty \cdot \|H\|_\infty$$
外乱抑圧制御
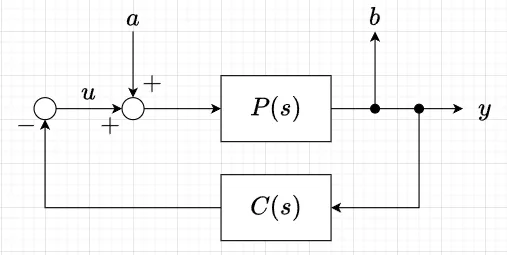
図3の制御系において、\(u\)を操作量、\(y\)を観測量、\(P(s)\)を制御対象、\(C(s)\)を制御器とする。入力点\(a\)に入ってくる外乱が出力点\(b\)に出来るだけ現れないように制御器\(C(s)\)を設計するのが外乱抑圧制御である。\(a\)点から\(b\)点までの伝達関数\(G_{ba}\)は、$$u=-yC= -bC ,\quad b= (u+a)P \\ b=(-bC+a)P = -PCb + Pa \\ b(I + PC) = Pa \\ \text{よって、} G_{ba}= (I + PC)^{-1} P$$となる。従って、\(a\)点の外乱が\(b\)点に出来るだけ現れないようにするには、なるべく小さい定数\(\gamma\)に対して、$$\|(I+PC)^{-1} P\|_{\infty} \lt \gamma$$とする\(C(s)\)を求めることになる。
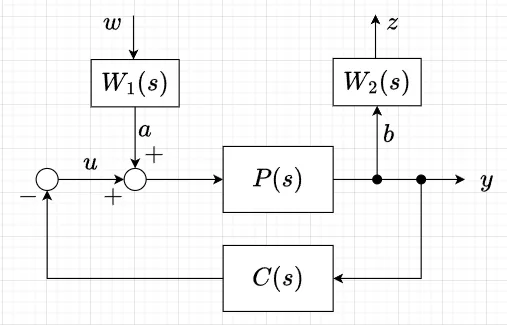
ここで、\(a\)点に入ってくる外乱の周波数特性が\(W_1(s)\)と分かっている場合、図4のように\(W_1\)を重み関数と考え、$$\|(I+PC)^{-1}P W_1\|_{\infty} \lt \gamma$$とすれば、より適切な制御器の設計ができる。また、出力端にも重み\(W_2(s)\)を付けて、$$\|W_2 (I+PC)^{-1} P W_1\|_{\infty} \lt \gamma$$とすれば、\(|W_2(j \omega)|\)を大きくとった周波数帯域で\(|(I+PC)^{-1} P W_1(j \omega)|\)を他の周波数帯域以上に小さくできる。これより、図4に示すように、仮想的な外乱\(w\)と仮想的な制御量\(z\)をその間の閉ループ伝達関数が$$G_{zw}(s) = W_2 (I+PC)^{-1} P W_1 $$となるように定義する。以上より、閉ループ系を安定にして、$$\|G_{zw}(s)\|_{\infty} \lt \gamma$$を満たす制御器\(C\)を設計することが、\(H_\infty\)制御問題となる。
ロバスト安定性
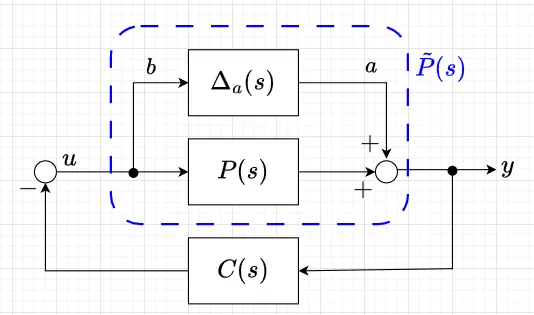
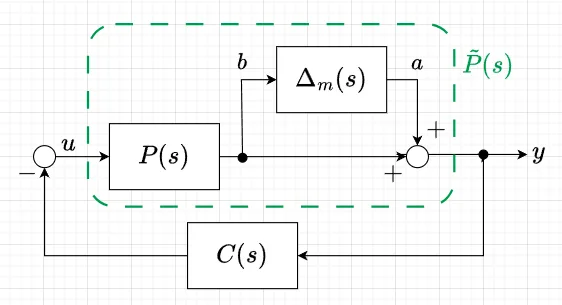
制御系を設計する際、制御対象の数学モデルを使うが、一般的に不確定な部分を無視してモデル化する。このモデルをノミナルモデルという。実際の系の制御対象を含めて安定な場合をロバスト安定という。ロバスト安定性を取り扱う場合、ノミナルモデル\(P(s)\)から変動した実際の制御対象\(\tilde{P}(s)\)を考える。図5は加法変動の場合を表している。つまり、$$\tilde{P}(s) = P(s) + \Delta_a(s)$$である。\(\Delta_a(s)\)を加法変動という。また、図6は乗法変動の場合を表している。このときは、$$\tilde{P}(s) = \{I + \Delta_m(s) \} P(s) \\ P(s) + \Delta_m (s)P(s)$$である。\(\Delta_m(s)\)を乗法変動という。乗法変動は\(\Delta_m\)は\(P\)の相対変動率を表している。機械系で高域の共振モードを無視してモデル化した場合などは、高域の共振モードは、加法変動として表せることになる。
ロバスト安定な系を構成するために、\(\Delta_a(s)\)が安定で、かつその大きさが既知なスカラ関数\(W_a(s)\)のゲインで抑える場合を考える。つまり、$$\bar{\sigma}\{\Delta_a(j\omega)\} \leq | W_a(j \omega)| \quad \forall \omega$$図5において、\(\Delta_a(s)\)を切り離したとして、点\(a\)から点\(b\)までの伝達関数を求めると、\(b = -CPb - Ca\)より、$$b = -(I+CP)^{-1}Ca \\ =-T_a(s) a$$となる。$$T_a(s) =(I+PC)^{-1}C = C(I+PC)^{-1}$$で、この\(T_a(s)\)を準相補感度関数という。
スモールゲイン定理
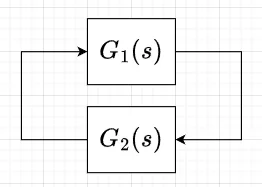
図において、\(G_1(s),\quad G_2(s)\)は安定かつプロパーであり、$$\|G_1(s) G_2(s)\|_\infty \lt 1$$を満たすものとする。このとき、図の閉ループ系も安定となる。
\(\Delta_a(s)\)、\(T_a(s)\)が安定で、$$\|-\Delta_a(s) T_a(s)\|_\infty \lt 1$$を満たせば、スモールゲイン定理よりロバスト安定である。さらに、既知な\(W_a\)を使って、$$\|W_a(s) T_a(s) \|_\infty \lt 1$$を満たされればロバスト安定が成立する。この式は、\(W_a(j \omega)\)が大きい周波数帯域では、制御器\(C\)のゲインを下げる必要があることを意味している。
図6に示す乗法変動の場合には、$$\bar{\sigma}\{\Delta_m(j \omega)\} \leq | W_m(j\omega)| \quad \forall \omega$$とすれば、ロバスト安定条件は、図6で\(\Delta_m = 0\)とおいたときの\(a,\;b\)間の閉ループ伝達関数を考え、$$\| W_m(s) T(s) \|_\infty \lt 1$$となる。ここで、$$T(s) = (I+ PC)^{-1}PC = P(I+CP)^{-1}C$$ は相補感度関数と呼ぶ。
混合感度問題
図7のフィードバック制御系で、\(r\):目標値、\(z_0\):制御量、\(e\):偏差とする。この制御系について、ロバスト安定で、偏差の小さい制御系の設計を考える。\(\Delta_a=0\)とすると、\(e = r-PCe\)より、$$e=S(s)r, \quad S(s) = (I+PC)^{-1} \;\;\; \cdots (7)$$である。\(S(s)\)を出力端の感度関数という。
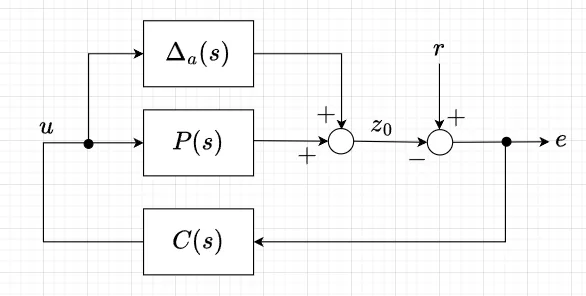
式(7)より、感度が低ければ一般に偏差が小さくなるといえる。従って、偏差にかける重みを\(W_s(s)\)とし、なるべく小さな\(\gamma\)に対して、$$\| W_s S\|_\infty \lt \gamma \;\;\; \cdots (8)$$とする制御器を構成する。重み\(W_s\)がスカラの場合を考えると、\(|W_s(j\omega)|\)が大きい周波数帯域で感度関数を小さくでき、偏差を抑制できる。なお、式(8)は、$$\| W_s S /\gamma \|_\infty \lt 1$$と規格化して扱える。
一方、ロバスト安定性を確保するには、加法変動の場合は、$$\| W_a T_a\|_\infty \lt 1$$であり、乗法変動の場合は、$$\|W_m T\| \lt 1$$を満たすように制御系を設計しなくてはならない。従って、$$S + PT_a = I,\quad S + T =I$$という関係が成り立つ。この関係より、同じ周波数帯域で同時に感度関数\(S\)と相補感度関数\(T\)を小さくするのは相反する要求である。また、\(P\)を固定した場合は、\(S\)と準相補感度関数\(T_a\)を小さくするのは相反する要求である。実際には、\(S\)の重み\(W_s(j \omega)\)は低周波数帯域で大きくとればよく、制御対象の変動を反映する\(W_a(j\omega),\;\; W_m(j\omega)\)は高周波帯域で大きくとればよい。よって、低周波帯域では\(S(s)\)を、高周波帯域では\(T_a(s)\)あるいは、\(T(s)\)を小さくするという設計指針が導かれる。このような問題を混合感度問題という。

