4. 制御数学基礎Ⅱ
内部安定の定義
図1のようにプロパーな制御対象\(G(s)\)とプロパーな制御器\(C(s)\)からなる閉ループ系の安定性を考える。ただし、\(\text{det}|I-CG| \neq 0\)と仮定する。このとき、\(G\)と\(C\)で不安定な極零相殺が生じず、かつ特定の入出力関係が安定な伝達関数で与えられるとき、内部安定という。内部安定のための必要十分条件は、図1のように各伝達関数の仮想の入力\(u_1,\; u_2\)、仮想の出力\(y_1,\;y_2\)を設定したとき、式(1)に示す\(u_1,\;u_2\)から\(y_1,\;y_2\)までの4つの伝達関数がプロパーで安定(\(RH_\infty\)関数)となることである。
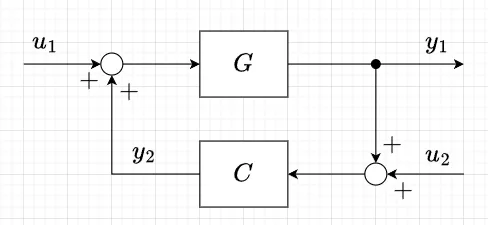
図1より、$$y_1 = GC y_1 + G u_1 + GC u,\quad y_2 = CG y_2 + CG u_1 + C u_2$$なので、$$y_1 = (I -GC)^{-1}G u_1 + (I-GC)^{-1}GC u_2 \\ y_2 = (I-CG)^{-1} CG u_1 +(I-CG)^{-1} Cu_2$$を得る。ここで、$$(I-GC)^{-1}G = G(I-CG)^{-1} \\ (I-GC)^{-1}GC = G(I-CG)^{-1}C \\ (I-CG)^{-1}CG = (I-CG)^{-1}-I$$の関係を使ってまとめると、$$\begin{bmatrix} y_1 \\ y_2 \end{bmatrix} = \begin{bmatrix} G(I-CG)^{-1} & G(I-CG)^{-1} C \\ (I-CG)^{-1}-I & (I-CG)^{-1}C \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} \;\;\; \cdots (1)$$となる。以上より、閉ループ系\((G,\;C)\)が内部安定であるための必要十分条件は、式(2)で表現できる。$$G(I-CG)^{-1},\quad G(I-CG)^{-1}C,\quad (I-CG)^{-1},\quad (I-CG)^{-1}C \in RH_\infty \;\;\;\cdots(2)$$初等的な古典制御では、\(u_1\)から\(y_1\)までの伝達関数\(G(I-CG)^{-1}\)が安定ならば閉ループ系は安定としているが、\(G,\;C\)の一方が不安定極を持ち、それが他方の零点で相殺されるとき(極零相殺)には内部安定ではないことに注意が必要である。
制御対象と制御器の双方が可安定かつ可検出のとき、閉ループ系全体を状態方程式で表すと、閉ループ系の\(A\)行列が安定行列であることが内部安定のための必要十分条件となる。ただし、制御対象、制御器が個別にもとから不安定な不可制御極や不安定な不可観測極を持っている場合には常に内部安定ではないので対象外とする。以下、制御対象は可安定、可検出、制御器は最小実現とする。
安定化条件
式(2)を満たす制御器\(C(s)\)を安定化制御器と定義する。\(C(s)\)の\(RH_\infty\)上の任意の右既約分解、左既約分解の\(V,U,\tilde{V},\tilde{U} \in RH_\infty\)により、$$C = UV^{-1} = \tilde{V}^{-1} \tilde{U}$$と表現する。既約分解なので、\(\alpha,\beta ,\gamma,\theta \in RH_\infty\)が存在し、ベズー方程式$$\alpha V + \beta U = I, \quad \tilde{V}\theta + \tilde{U} \gamma =I$$を満たす。式(2)の4つの伝達関数は、\(G = NM^{-1},\; C = \tilde{V}^{-1} \tilde{U}\)を代入した$$(I - CG)^{-1]}= (I - \tilde{V}^{-1} \tilde{U} N M^{-1})^{-1} \\ = M \Delta^{-1} \tilde{V}, \quad \Delta = \tilde{V}M - \tilde{U}N \in RH_\infty$$を使い、$$(I - CG)^{-1} = M \Delta^{-1} \tilde{V} \\ (I - CG)^{-1}C = M \Delta^{-1} \tilde{U} \\ G(I - CG)^{-1} = N \Delta^{-1} \tilde{V} \\ G(I-CG)^{-1} C = N \Delta^{-1} \tilde{U}$$となる。従って、式(2)は、$$\begin{bmatrix} M \\ N\end{bmatrix}\Delta^{-1} \begin{bmatrix} \tilde{V} & \tilde{U}\end{bmatrix} \equiv \epsilon\;\;\; \cdots (3)$$とおき、\(\epsilon \in RH_\infty\)(プロパーで安定な関数)の条件にまとめられる。
ベズー方程式
伝達関数を\(G(s)=N(s) M(s)^{-1}\)として、ベズー方程式$$X(s) M(s) + Y(s) N(s) = I$$が成立するとき、\(N(s)\)と\(M(s)\)は互いに素(共通因子を持たない)である。(\(X(s),\;Y(s)\)は補因子)
\(N(s)\)と\(M(s)\)に共通因子\(J(s)\neq 1\) があるとすると、\(N(s) = J(s) N'(s)\)、\(M(s) = J(s) M'(s)\) と表せる。これをベズー方程式に代入すると$$X(s) J(s) M'(s) + Y(s) J(s) N'(s) = I$$となる。左辺は\(J(s)\)を因子として含むため、右辺も\(J(s)\)を因子として持たなければならないが、右辺は単位行列\(I\)であり、因子を持つことはあり得ない。以上の矛盾により、ベズー方程式が成立するとき、\(N(s)\)と\(M(s)\)は共通因子を持たないといえる。
ここで、\(\Delta^{-1} \in RH_\infty\)ならば、\(\epsilon \in RH_\infty\)が成り立つ。逆に\([\tilde{X} \quad -\tilde{Y}],\quad [\theta^T \quad \gamma^{T}]^T\)を式(3)に左右からかければ、$$\Delta^{-1} = \begin{bmatrix} \tilde{X} & - \tilde{Y} \end{bmatrix} \epsilon \begin{bmatrix} \theta \\ \gamma \end{bmatrix}$$ を得る。つまり、\(\epsilon \in RH_\infty\)のとき\(\Delta^{-1} \in RH_\infty\)でなくてはならない。よって、\(C\)が安定化制御器であるための必要十分条件は、\(\Delta\)がユニモジュラとなることである。
安定化制御器の条件
プロパーな伝達関数\(G(s)\)の既約分解のもとで、\(C(s) = U(s)V^{-1}(s) = \tilde{V}^{-1}(s) \tilde{U}(s)\)で表された制御器\(C(s)\)が安定化制御器であるための必要十分条件は、$$\Delta(s) = \tilde{V}(s) M(s) - \tilde{U}(s) N(s) \\ \text{あるいは} \tilde{\Delta}(s) = \tilde{M}(s) V(s) - \tilde{N}(s) U(s)$$がユニモジュラとなることである。
\(\Delta\)はユニモジュラなので、制御器\(C(s)\)の既約分解\(\tilde{V}^{-1} \tilde{U}\)において、\(\tilde{V}\)を\(\Delta^{-1} \tilde{V}\)、\(\tilde{U}\)を\(\Delta^{-1} \tilde{U}\)と正規化したものに置き換え、$$C =(\Delta^{-1} \tilde{V})^{-1} (\Delta^{-1} \tilde{U})$$と分解することを考える。このとき、$$\Delta^{-1}(s) \Delta(s) = \Delta^{-1}(s) \tilde{V}(s) M(s) - \Delta^{-1}(s)\tilde{U}(s) N(s)= I$$となる。よって、\(C(s)\)が安定化制御器であるための必要十分条件は、$$\tilde{V}(s)M(s) - \tilde{U}(s)N(s) =I \\ \text{あるいは} \tilde{M}(s)V(s) - \tilde{N}(s)U(s) =I$$ を満たすものが存在することである。
安定化制御器のパラメータ表現
プロパーな伝達関数\(G\)の二重既約分解のもとで、安定化制御器\(C\)のすべてのクラスを自由パラメータ\(Q\)を使って表す。\(K = \tilde{V}^{-1} \tilde{U}\)を安定化制御器とすると、$$\tilde{V}(s)M(s) - \tilde{U}(s)N(s) = \begin{bmatrix} \tilde{V} & - \tilde{U} \end{bmatrix} \begin{bmatrix} M \\ N \end{bmatrix} = I \;\;\; \cdots (4)$$を満たす\(\tilde{V},\; \tilde{U}\)が存在する。ここで、\(G(s)\)は二重既約分解できるので、補因子\(X,Y,\tilde{X},\tilde{Y} \in RH_\infty\)が存在し、$$\begin{bmatrix} \tilde{X}(s) & -\tilde{Y}(s) \\ -\tilde{N}(s) & \tilde{M}(s) \end{bmatrix} \begin{bmatrix} M(s) & Y(s) \\ N(s) & X(s) \end{bmatrix} = I \;\;\; \cdots (5)$$が成り立つ。式(5)を満たす\(X,\; Y\)を使って、$$\begin{bmatrix} \tilde{V} & -\tilde{U} \end{bmatrix} \begin{bmatrix} M & Y \\ N & X \end{bmatrix} = \begin{bmatrix} I & Q \end{bmatrix} \;\;\; \cdots (6)$$とおく。すると、\(\tilde{V},\;\tilde{U},\;X,\;Y\)はすべて\(RH_\infty\)に属するので、\(Q \in RH_\infty\)となる。式(5)の関係を使って、式(6)の係数行列の逆をとると$$\begin{bmatrix} \tilde{V} & - \tilde{U}\end{bmatrix} = \begin{bmatrix} I & Q \end{bmatrix} \begin{bmatrix} \tilde{X} & - \tilde{Y} \\ - \tilde{N} & \tilde{M} \end{bmatrix} = \begin{bmatrix} \tilde{X} - Q\tilde{N} & -\tilde{Y} + Q \tilde{M} \end{bmatrix}\;\;\; \cdots (7)$$を得る。これは、任意の\(Q \in RH_\infty\)に対して、式(7)を満たす\(\tilde{V},\; \tilde{U}\)は、\(\tilde{V}, \tilde{U} \in RH_\infty\)を満たし、式(4)を満たす。従って、$$K(s) = \tilde{V}^{-1} \tilde{U} = (\tilde{X} - Q\tilde{N})^{-1} (\tilde{Y} - Q \tilde{M}) \;\;\; \cdots (8)$$も安定化制御器となり、式(8)が安定化制御器のパラメータ表現となる。

