5. 制御数学基礎Ⅲ
※状態フードバックやオブザーバについては、システム制御の14. 15. 16. 17.を参照願います。
状態フィードバック、オブザーバと二重既約分解
制御対象は、式(1)で示すように厳密にプロパーとする。$$G(s) = \{A,B,C,0\} \\ \dot{x} = Ax + Bu ,\quad y = Cx \;\;\; \cdots (1)$$また、不安定な隠れモードがないように\((A,B)\)は可安定、\((A,C)\)を可検出とする。
状態変数\(x\)を全て測定可能と仮定して、式(2)の状態フードバックにより安定化する。$$u = Fx + v \;\;\; \cdots (2)$$このとき、閉ループシステムは、\(A_F = A+BF\)とおいて、式(3)となる。$$\dot{x} = A_F x + Bv, \quad y=Cx \;\;\; \cdots(3)$$ フィードバックゲイン\(F\)は、\(A_F=A+BF\)を安定とするように選ぶ。\(v -u\)間と\(v-y\)間の関係は、式(4)となる。$$u = \{I + F(sI-A_F)^{-1}B\}v \equiv M(s) v \\ y=C(sI-A_F)^{-1}B v \equiv N(s) v \;\;\; \cdots(4)$$ 式(4)の両式から\(v\)を消去すると、\(y = N M^{-1} u\)となるので、$$G(s) = y u^{-1} = N M^{-1}$$となり、\(G\)の右既約分解の候補が得られる。
次に、式(1)で\(x\)が直接測定できない場合、\(x\)の推定値を\(\hat{x}\)として安定化制御を\(u = F \hat{x}\)で実現する。\(\hat{x}\)は、式(5)のオブザーバにより決定する。$$\dot{\hat{x}} = A \hat{x} + B u + H(C\hat{x} - y) = A_H \hat{x} -H y + B u \;\;\; \cdots (5)$$ ここで、\(A_H = A + HC\)とおいた。\(H\)は\(A_H\)を安定にするように選ぶ。以上より、$$u = F \hat{x} ,\quad \dot{\hat{x}} = (A_H + BF)\hat{x} - Hy$$とまとめられ、\(y-u\)間の制御器\(C_o\)は、式(6)となる。$$C_o(s) = -F(sI - A_H -BF)^{-1} H \;\;\; \cdots (6)$$この制御器\(C_o\)は式(7)の左既約分解の候補を持つ。$$C_o = \tilde{X}^{-1} \tilde{Y} \\ \tilde{X} = I-F(sI - A_H)^{-1}B, \quad \tilde{Y} = -F(sI-A_H)^{-1}H \;\;\; \cdots (7)$$
\(G(s) = \{A,B,C,0\}\)とし、\((A,B)\)を可安定、\((A,C)\)を可検出とする。このとき二重既約分解を満たすパラメータは、\(A_F = A+BF,\quad A_H = A+ HC\)を安定にするように\(F,\;H\)を選ぶと、式(8)で与えられる。$$M = \left[\begin{array}{c|c} A_F & B \\ \hline F & I \end{array}\right] , \quad N =\left[\begin{array}{c|c} A_F & B \\ \hline C & 0 \end{array}\right] $$ $$ \tilde{X} = \left[\begin{array}{c|c} A_H & -B \\ \hline F & I \end{array}\right] , \quad \tilde{Y} =\left[\begin{array}{c|c} A_H & -H \\ \hline F & 0 \end{array}\right] $$ $$ \tilde{M} = \left[\begin{array}{c|c} A_H & H \\ \hline C & I \end{array}\right] , \quad \tilde{N} =\left[\begin{array}{c|c} A_H & B \\ \hline C & 0 \end{array}\right] $$ $$ X = \left[\begin{array}{c|c} A_F & H \\ \hline -C & I \end{array}\right] , \quad Y =\left[\begin{array}{c|c} A_F & H \\ \hline -F & 0 \end{array}\right] \\ \;\;\; \cdots (8)$$
二重既約分解
プロパーなすべての伝達関数\(G(s)\)は、右既約な\(M,\;N \in RH_\infty\)と左既約な\(\tilde{M},\;\tilde{N} \in RH_\infty\)を使って、式(A)のように\(RH_\infty\)上の右既約分解と左既約分解ができる。$$G(s) = N(s) M^{-1}(s) \\ = \tilde{M}^{-1}(s) \tilde{N}(s) \;\;\; \cdots(A)$$このとき、補因子行列\(X,Y, \tilde{X}, \tilde{Y} \in RH_\infty\)が存在し、式(B)が成り立つ。$$\begin{bmatrix} \tilde{X}(s) & - \tilde{Y}(s) \\ -\tilde{N}(s) & \tilde{M}(s) \end{bmatrix} \begin{bmatrix} M(s) & Y(s) \\ N(s) & X(s) \end{bmatrix} = I \\ \;\;\; \cdots (B)$$式(B)が成り立つとき、式(A)を\(G(s)\)の二重既約分解という。
[安定化制御器の例]\(G(s) = 1/(s-3)\)としたときの安定化制御器を求める。
状態方程式、出力方程式は、\(\dot{x} = 3x+u ,\quad y=x\)なので、\(A=3,\;B=1,\;C=1,\;D=0\)となる。状態フィードバックゲインを\(F=-4\)、オブザーバゲインを\(H=-5\)と選び、\(A_F=A+BF=-1,\; A_H=A+HC=-2\)とする。
\(Q\)をパラメータとした安定化制御器
\(G(s)\)の二重既約分解のもとで、\(G(s)\)のすべての安定化制御器は、\(Q(s) \in RH_\infty\)をパラメータとして、$$C(s) = (\tilde{X}- Q\tilde{N})^{-1}(\tilde{Y} -Q \tilde{M})\\: \text{det}|\tilde{X} - Q \tilde{N}| \neq 0 $$ $$C(s) = (Y-MQ)(X-NQ)^{-1} \\: \text{det}|X-NQ| \neq 0$$と表現できる。
式(8)より、$$M = \left[\begin{array}{c|c} -1 & 1 \\ \hline -4 & 1 \end{array}\right] = \frac{s-3}{s+1} , \quad N =\left[\begin{array}{c|c} -1 & 1 \\ \hline 1 & 0 \end{array}\right]=\frac{1}{s+1} , \\ \tilde{X} = \left[\begin{array}{c|c} -2 & -1 \\ \hline -4 & 1 \end{array}\right] = \frac{s+6}{s+2} , \quad \tilde{Y} =\left[\begin{array}{c|c} -2 & 5 \\ \hline -4 & 0 \end{array}\right]=\frac{-20}{s+2} ,\\ \tilde{M} = \left[\begin{array}{c|c} -2 & -5 \\ \hline 1 & 1 \end{array}\right] = \frac{s-3}{s+2} , \quad \tilde{N} =\left[\begin{array}{c|c} -2 & 1 \\ \hline 1 & 0 \end{array}\right]=\frac{1}{s+2} , \\X = \left[\begin{array}{c|c} -1 & -5 \\ \hline -1 & 1 \end{array}\right]=\frac{s+6}{s+1} , \quad Y =\left[\begin{array}{c|c} -1 & -5 \\ \hline 4 & 0 \end{array}\right]=\frac{-20}{s+1} $$となる。よって、安定化制御器は\(Q \in RH_\infty\)に対して、$$C(s) = (Y-MQ)(X-NQ)^{-1} =\left(\frac{-20}{s+1} - \frac{s-3}{s+1}Q\right) \left(\frac{s+6}{s+1} - \frac{1}{s+1}Q\right)^{-1} = -\frac{20+Q(s-3)}{s+6-Q}$$と求まる。
自由パラメータ\(Q\)の機能
状態フードバックとオブザーバによる安定化制御器の構成における自由パラメータ\(Q \in RH_\infty\)の機能を考える。オブザーバの推定状態変数\(\hat{x}\)から計算できる推定出力\(\hat{y}\)は、式(9)となる。$$\dot{\hat{x}} = A_H \hat{x} - Hy + Bu \\ \hat{y} = C \hat{x} \;\;\; \cdots (9)$$この式をラプラス変換して整理すると、$$\hat{x} = -(sI-A_H)^{-1} Hy + (sI-A_H)^{-1}Bu \\ \hat{y} = -C(sI-A_H)^{-1}Hy +C(sI - A_H)^{-1}Bu \\ = (I - \tilde{M})y + \tilde{N}u$$となる。
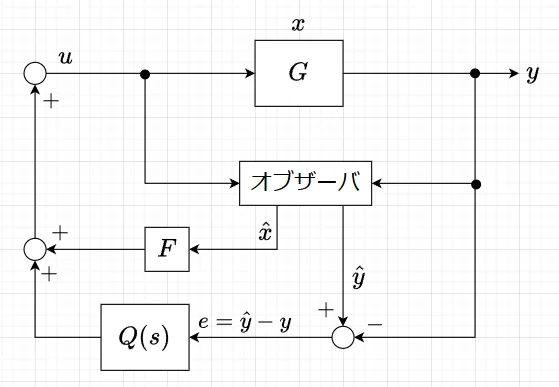
これより、推定出力偏差\(e\)は、\(e = \hat{y} - y= -\tilde{M}y + \tilde{N}u\)と表せる。
オブザーバによる状態フィードバックでは、操作量は\(u=F\hat{x}\)であるが、これに図1に示すように\(Qe\)を加えると、$$u = F \hat{x} + Qe =-F(sI-A_H)^{-1}Hy + F(sI-A_H)^{-1}Bu + Qe \\ = \tilde{Y}y + (I-\tilde{X})u + Q(-\tilde{M} y + \tilde{N}u)$$となる。これより、$$(\tilde{X} - Q \tilde{N})u = (\tilde{Y} -Q\tilde{M})y \\ u=(\tilde{X} - Q \tilde{N})^{-1}(\tilde{Y} -Q \tilde{M})y$$となるので、制御器として$$C(s) = (\tilde{X} - Q \tilde{N})^{-1} (\tilde{Y} -Q \tilde{M})$$を得る。これは、「\(Q\)をパラメータとした安定化制御器」である。つまり、図1のように従来の同一次元オブザーバによる状態フィードバックに推定出力偏差\(e\)のループを新たに加え、\(u\)に\(Qe\)を加えることで、全ての安定化制御器を表現できることを意味している。

