9. 電磁力
電磁力とは、基本的に電荷を持つ粒子が互いに及ぼし合う力、または電流が磁場から受ける力のことを指す。電磁力の特徴は、遠隔力、引力と反発力、距離の二乗に反比例、であり、電磁力の種類は大きく分けて、静電気力(クーロンの法則)と磁力(フレミングの左手の法則や右ねじの法則など)である。ここでは、磁界中の電流に働く力について考える。
磁界と電流の間に働く力
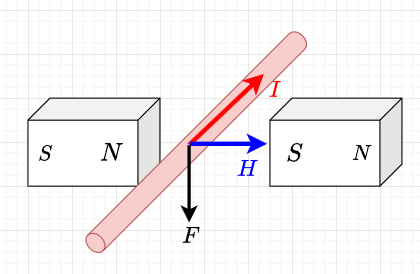
図1に示すように、磁石のN極とS極との磁極間に生じる磁界\(H\)(青矢印)中で、磁界と直角に導線を置き、赤矢印の方向に電流\(I\)を流すと、電流が流れる導線には黒矢印の方向に力\(F\)が働く。このように、磁界中にある電流に作用する力を電磁力という。
電磁力が発生する原理は、次のように説明できる。図2に示すように、磁極による磁界(磁力線:青矢印)はNからSへ平行に存在するものとする。この磁界中に直角に流れる電流(図のX印は電流の向きが画面の表から裏を意味する。)によって、電流の周りには右ネジの法則に従って同心円状の磁力線(黒で示す矢印)が生じる。この二つの磁力線(青の矢印と黒の矢印)を合成すると、電流の上側では磁界の強さが大きくなり、電流の下側では磁界の強さが小さくなる。
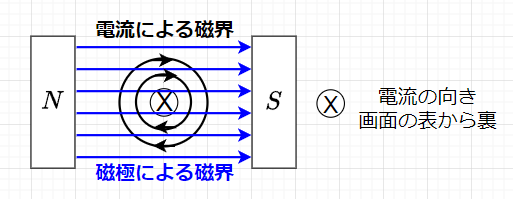
つまり、電流の上側の磁界エネルギーは大きくなり、電流の下側の磁界エネルギーは小さくなる。この結果、磁界エネルギーの差により、磁界エネルギーの大きい方から小さい方へ力を受けることになる。従って、磁界の方向と同じ方向に電流を流しても磁界エネルギーの差が生じないので、力は生じない。
フレミングの左手の法則
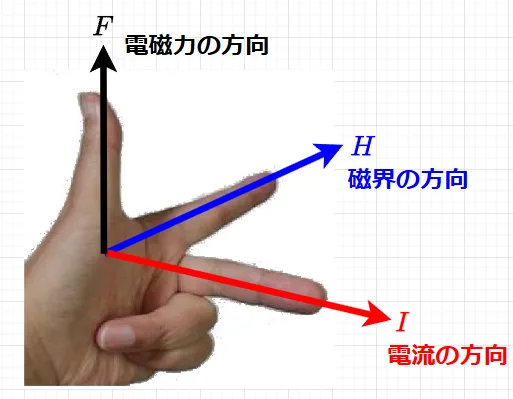
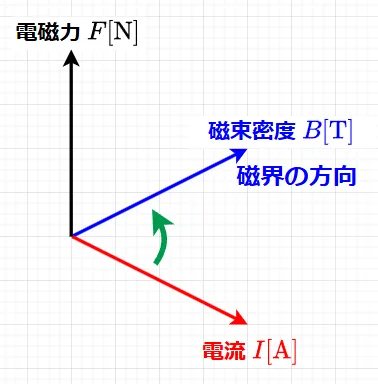
フレミングの左手の法則は、磁界中にある電流に働く力の方向を表現するために考えられたもので、図3のように左手の人差し指、中指を互いに直角に曲げ、人差し指を磁界\(H\)、中指を電流\(I\)に一致するように向けたとき、親指の向きに電磁力\(F\)が働くことを表したものである。
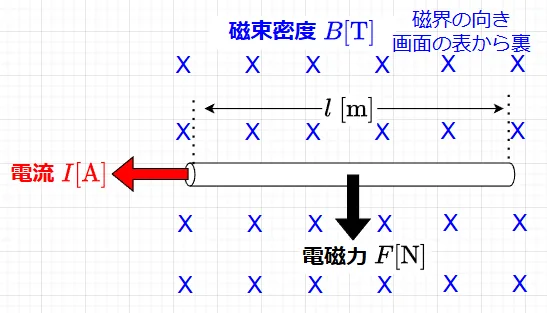
図4に示すような磁束密度が\(B\;\)[T]の平等磁界に長さ\(l\;\)[m]の導線を直角に置いたときの電流(導線)に働く電磁力\(F\)の大きさは、$$F=IBl \;\;[\text{N}]\;\;\; \cdots(1)$$となる。電磁力は、磁束密度\(B\)と電流\(I\)が大きいほど大きくなる。
\(F,\;I,\;B\)をベクトルとして考えると、電磁力\(F\)はベクトル積(ベクトルの外積)で表せ、式(2)となる。$$F = (I \times B)l \;\;\;\cdots (2)$$
式(2)より、図5に示すように、磁界中にある電流に働く電磁力\(F\)の方向は、電流\(I\)のベクトルを磁界の方向に回転させた(図の緑の矢印の方向へ回転)時の右ネジの進む方向(右ネジの法則)となる。これを3本の指で表したのがフレミングの左手の法則なので、右ネジの法則が理解できていれば、3本の指の向きで手首が捻じれてしまうフレミングの左手の法則は無用である。また、電(電流)から磁(磁界)の方向に右手の4本の指を折り曲げたときの親指の方向が力(電磁力)となるので、電→磁→力(電磁力)で記憶すれば、左手のどの指が電流なのか、磁界なのか悩む必要もない。
電流相互間に働く力
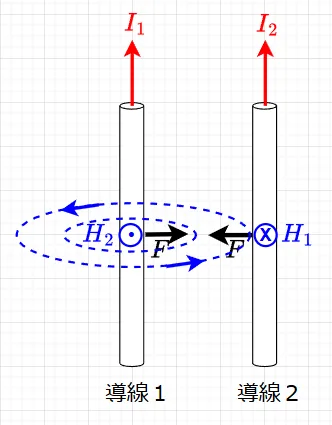
図6に示すように、2本の平行に配置された導線があり、それぞれに電流が流れていると、同一方向の電流の場合には、導線同士が吸引される方向に力が働き、反対方向の電流の場合には、導線同士が反発する方向に力が働く。
これは、一方の電流によりその周りに磁界が発生し、その磁界中に他方の電流があるため、フレミングの左手の法則に従って電磁力が働くためと考えられる。図6では、導線1に電流\(I_1\)が流れることで磁界\(H_1\)が生じ、その磁界\(H_1\)は導線2を画面の表から裏方向に貫く。磁界\(H_1\)中に電流\(I_2\)が流れるので電磁力\(F\)は左方向に働く。一方、導線2に電流\(I_2\)が流れることで磁界\(H_2\)が生じ、その磁界\(H_2\)は導線1を画面の裏から表方向に貫く。磁界\(H_2\)中に電流\(I_1\)が流れるので電磁力\(F\)は右方向に働く。以上により、導線1,2には吸引力が働いているように見える。
導線1,2に流れる電流の方向が反対方向の場合は、反発力が働くように見える。
電流相互間に働く力の大きさ
十分に長い直線電流間に働く力の大きさを考える。真空中に置いた十分に長く、間隔\(r\;\)[m]の平行な導線に、それぞれ\(I_1,\;I_2\)の電流が流れているとき、電流\(I_1\)によって、\(I_2\)のところに生ずる磁界の強さを\(H_1\)とすると、アンペアの法則より、$$H_1 = \frac{I_1}{2\pi r} \;\;[\text{A/m}]$$となる。その方向は2導線を含む面に直角である。従って、電流\(I_2\)が流れる導線\(1\;\)[m]当たりに作用する力の大きさは、$$F = I_2 \mu_0 H_1 = \mu_0 \frac{I_1 I_2}{2 \pi r} \;\;[\text{N/m}]$$である。また、\(\mu_0 = 4 \pi \times 10^{-7}\)であるから、$$F = \frac{2 I_1 I_2}{r} \times 10^{-7} \;\;[\text{N/m}]$$となる。電流\(I_1\)が流れる導線に働く力も同様である。
この結果は、SI単位系における電流の基準値を定める根拠に利用されている。つまり、「1[m]の間隔に置かれた平行導線に同じ電流を流したとき、導線の単位長さ(1[m])当たりに働く力の大きさが\(2\times 10^{-7} \;\)[N]であるときの電流の大きさを1[A]と定義する。」である。
磁界中で運動する荷電粒子に作用する力
荷電粒子が磁界中に静止しているときには、荷電粒子は何の作用も受けない。ところが、磁界中で荷電粒子が運動すると、荷電粒子に電磁力に相当する力が作用する。荷電粒子を正電荷とすると、電流が運動方向に流れるということになる。従って、図7に示すようにフレミングの左手の法則に従って電磁力\(F\)が作用することになる。
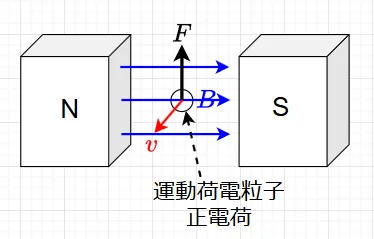
いま、磁束密度\(B\;[T]\)の磁界中に荷電粒子(正電荷)\(q\;[C]\)が\(v\;\)[m/s]の速度で磁界に直角に突入したときの荷電粒子が受ける力\(F\;\)[N]を求める。
1個の電荷が\(v = \Delta x/\Delta t\;\)[m/s]の速度で運動するとすれば、\(\Delta t\;\)[s]の間に\(\Delta x\;\)[m]の距離進むのだから、\(\Delta x\;\)[m]の長さの導体に$$I = \frac{\Delta q}{\Delta t} \;[\text{A}]$$の電流が流れていると考えることができる。従って、磁束密度を\(B\)、電流を\(I\)、電流の長さを\(l\)とするときの電磁力は、$$F = B I l\;[\text{N}]$$なので、荷電粒子に働く力は、$$F = B \cdot \frac{q}{\Delta t} \cdot \Delta x = q \cdot \frac{\Delta x}{\Delta t}\cdot B $$よって、$$F =q vB \;[\text{N}]$$と表せる。なお、\(F\;v,\;B\)はベクトルなので、ベクトルの外積を使って、$$F =q(v \times B) \;[\text{N}]$$と力の方向もまとめて表せる。
荷電粒子が電子\(e\)の場合、作用する力\(F\)は、\(q=-e \;\)[C]なので、$$F = e(-v \times B) \;[\text{N}]$$となる。

