12. 電磁波

変位電流

電流が至るところで連続であるとするために、電荷の移動による電流と電界の変化に伴う電流を考える。この電界の変化に伴う電流を変位電流という。変位電流は、時間変化する電場が作る「見かけの電流」 と言うこともある。この変位電流の導入により、電磁波の存在が理論的に導かれた。

図１は、伝導電流と変位電流の違いの模式図である。図１に示すように、コンデンサ（２枚の極板）に時間とともに変化する電圧（交流電圧）を加える。図１(a)のように、上の電極側が\(+\)（高い電位）、下の電極側が\(-\)（低い電位）のときは、電荷が電源から移動し、コンデンサには充電電流\(i\)が図１(a)の方向に流れる。次に、図１(b)のように下の電極側が\(+\)（高い電位）、上の電極が\(-\)（低い電位）になるときは、最初に充電された電荷が逆向きに移動（放電）し、下の電極側が\(+\)、上の電極側が\(-\)に充電電流\(i\)が流れる。

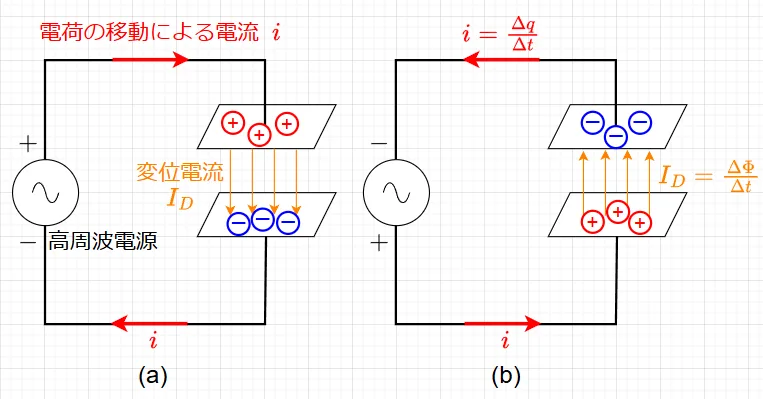
このように、コンデンサに交流電圧を印可すると、充電、放電の繰り返しによって、電極間が真空（もしくは絶縁）されていても連続的に電流が流れる。電流\(i\)は、電荷の移動、すなわち電荷の時間に対する変化の割合なので、$$i = \frac{\Delta Q}{\Delta t}, \quad i=\frac{dQ}{dt}$$であり、電荷\(Q = CV\)の関係から$$i = C\frac{\Delta V}{\Delta t}, \quad i=C\frac{dQ}{dt}$$となる。すなわち、印可する電圧の時間変化（\(\Delta V / \Delta t\)）が大きいほど電流が大きいことになる。
コンデンサと電源を接続する導線には電荷が移動し、電流\(i\)が流れるが、この電流により磁界が発生する。コンデンサの電極間隙の部分は、真空（もしくは絶縁）なので電荷の移動はない。しかし、電極間隙の部分には電流がないにもかかわらず、その周りには磁界が存在するので、アンペアの法則が成り立つ。つまり、電極間には電荷の移動による電流は存在しないが、電極に存在する電荷による電束が発生している。電荷\(Q\)と電束\(\Phi_D\)とは、\(\Phi_D =Q\)の関係があるから、$$I_D = \frac{\Delta Q}{\Delta t} = \frac{\Delta \Phi_D}{\Delta t}$$となる。よって、電流には以下の２種類が考えられる。
・\(i=\Delta Q / \Delta t\)：導体中を流れる電流、伝導電流。
・\(I_D = \Delta \Phi_D / \Delta t\)：電束の時間変化による電流、変位電流。
この変位電流を定義することで、「電流はあらゆるところで連続である」ということになる。

電磁波の発生原理

電磁波は、電界と磁界とが互いに鎖交し合って存在する一種の波動であり、変位電流の磁気作用と誘導電界を生じる電磁誘導の現象との相互作用によるものである。
図２に示すように電極間隔の広いコンデンサに\(\Delta V / \Delta t\)の大きな電源（高周波電源）を接続した場合を考える。

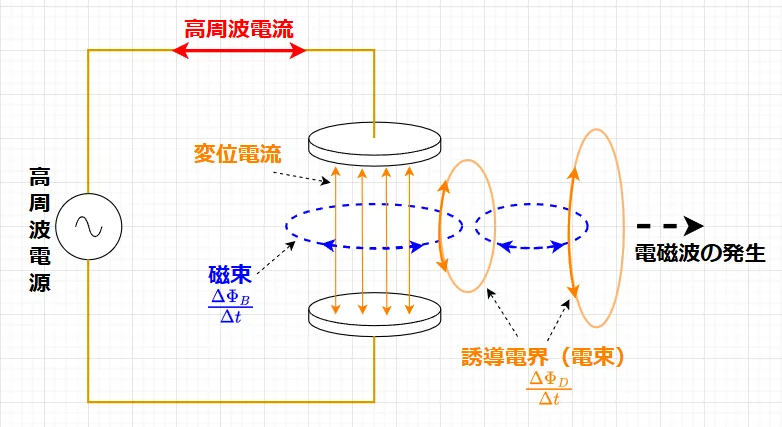
高周波電源なので、コンデンサへ流れる高周波電流は大きく、その結果、電極間隙に大きな変位電流が流れる。この変位電流により、その周りには磁界\(H\)が生じる。\(B = \mu_0 H\)の関係なので、磁束\(\Phi_B\)が生じるともいえる。変位電流は高周波交流によるものなので、変位電流によって生じる磁束\(\Phi_B\)も高周波数で変化する。この磁束\(\Phi_B\)の変化\(\Delta \Phi_B / \Delta t\)により、反作用的に誘導電界\(E_i\)が生じる。\(D = \epsilon E\)の関係より、電束\(\Phi_D\)が生じるともいえる。この電束の変化\(\Delta \Phi_D / \Delta t\)により磁界が発生し、互いの作用が繰り返されることになる。この現象は、進行波となって外向きに伝搬していく。このようにして生じた電界と磁界の相互作用の波動が電磁波である。