8-1. データの補間
最小二乗法は、測定値群を多項式などの尤もらしい関数曲線で表す手段であるが、必ずしも測定点を通るものではない。とびとびの実験データを得た時は、それらの中間点を推定したり、点列を繋いでなめらかな曲線を描いたりする必要もある。これらの手法をデータ補間、曲線近似という。
ラグランジュの補間法
ラグランジュ補間法は、与えられたデータ点を通る1つの多項式を求める方法 である。これは、ニュートン補間法と並ぶ代表的な補間手法の1つであり、特に数値解析や信号処理の分野で用いられる。
\(n+1\) 個の異なるデータ点 \((x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n)\) が与えられたとき、
ラグランジュ補間多項式 \(P_n(x)\)は式(1)で表される。$$P_n(x) = \sum_{k=0}^{n} y_k L_k(x) \;\;\; \cdots(1)$$ここで、ラグランジュ基底多項式 \(L_k(x)\)は次のように定義される。$$L_k(x) = \prod_{j=0 \\ j \neq k}^{n} \frac{x - x_j}{x_k - x_j}$$\(L_k(x)\)は \(x_k\)で 1 になり、それ以外のデータ点では 0 になる 。式(1)により、補間多項式 \(P_n(x)\)はすべてのデータ点\((x_k, y_k)\)を正確に通る。
[例]3つのデータ点\((1, 2), (3, 4), (5, 6)\)をラグランジュの補間法で補間することを考える。
ラグランジュ基底多項式 は、$$L_0(x) = \frac{(x-3)(x-5)}{(1-3)(1-5)}=\frac{1}{8}(x-3)(x-5)\\ L_1(x) = \frac{(x - 1)(x - 5)}{(3 - 1)(3 - 5)}=-\frac{1}{4}(x-1)(x-5)\\L_2(x) = \frac{(x - 1)(x - 3)}{(5 - 1)(5 - 3)}=\frac{1}{8}(x-1)(x-3)$$となる。
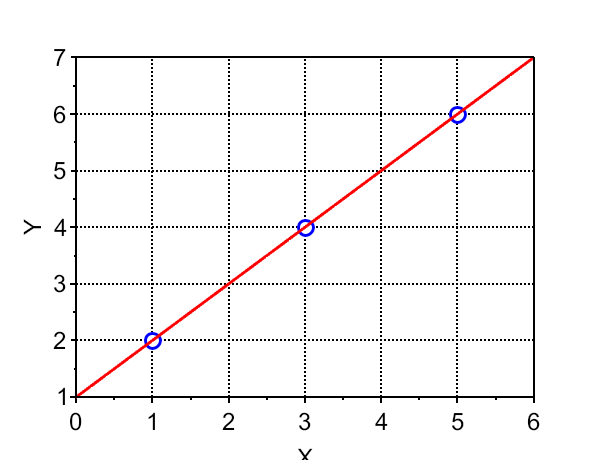
よって、補間多項式 \(P_2(x)\)は、$$P_2(x) = 2 L_0(x) + 4 L_1(x) + 6 L_2(x)=x+1$$となる。この場合は、一次関数(直線)の式となる。図1にグラフを示す。図の青点がデータ点、赤線が\(P_2(x)\)による補間線である。
ラグランジュの補間の利点は、任意の点を正確に通る多項式を求められる、係数の計算が直接できるため行列の解法を必要としない、計算プロセスがシンプルで実装しやすい、などがある。 欠点としては、高次補間では振動が激しくなる(データ点が増えると端での振動が大きくなる)問題がある。また、計算コストが高く\(O(n^2)\)の計算量が必要のため大量のデータには向かない。
ニュートンの補間法
ニュートン補間法は、与えられたデータ点を通る多項式を求める補間手法 で、ラグランジュ補間法と異なり逐次的に計算ができるため、計算コストが低く拡張しやすい という特徴がある。
\(n+1\) 個のデータ点 \((x_0, y_0), (x_1, y_1),\ldots, (x_n, y_n)\)に対して、ニュートン補間多項式\(P_n(x)\)は式(2)にる。$$P_n(x) = a_0 + a_1(x - x_0) + a_2(x - x_0)(x - x_1) +\cdots + a_n(x - x_0)(x - x_1) \cdots (x - x_{n-1})\;\;\; \cdots(2)$$このとき、係数 \(a_k\)は差分商を用いて計算する。
・0次差分商(与えられたデータ点の\(y\)値)$$f[x_k] = y_k$$
・1次差分商$$f[x_i, x_j] = \frac{f[x_j] - f[x_i]}{x_j - x_i}$$
・2次差分商$$f[x_i, x_j, x_k] = \frac{f[x_j, x_k] - f[x_i, x_j]}{x_k - x_i}$$
・一般の\(n\)次差分商$$f[x_0, x_1, ..., x_n] = \frac{f[x_1, ..., x_n] - f[x_0, ..., x_{n-1}]}{x_n - x_0}$$この差分商を使って、補間多項式の係数\(a_k\)を求める。
[例]3つのデータ点\((1, 2), (3, 4), (5, 6)\)をニュートンの補間法で補間することを考える。
0次の差分商は元の\(y\)値$$f[1] = 2, \quad f[3] = 4, \quad f[5] = 6$$1次の差分商$$f[1,3] = \frac{4 - 2}{3 - 1} = 1, \quad f[3,5] = \frac{6 - 4}{5 - 3} = 1$$2次の差分商$$f[1,3,5] = \frac{1 - 1}{5 - 1} = 0$$よって、この場合の補間多項式は、$$P_2(x) = 2 + 1(x - 1) + 0(x - 1)(x - 3)= 2 + (x - 1)=x+1$$と1次関数(直線)となり、3点を通る関数になる。
ニュートンの補間法の利点は、計算が効率的(逐次的に係数を求められるため、追加計算が容易)、データ点を増やすのが簡単(新しい点を加えても既存の計算を無駄にしない)などである。欠点は、高次補間では誤差が大きくなることがある、ラグランジュの補間法より数式が煩雑になる、大きな\(n\)では差分商による計算誤差の蓄積が発生する、などがある。
以上より、逐次的に計算できるため大規模データにも適用しやすいので、動的にデータ点が増える場合に適した手法といえる。
スプライン補間法
スプライン補間法は、データ点を通る滑らかな曲線を作成する補間手法で、高次の多項式補間(例:ラグランジュの補間法)では振動が大きくなりやすいため、スプライン補間を使うことで、局所的に滑らかな関数をつなぎ合わせる 方法が用いられる。また、データ点の間隔が不均一な場合や、曲線が急激に変化する場合に有効である。
スプライン補間法では、区分的な多項式(通常は3次多項式)を用いて、データ点間を滑らかに繋ぐ。各区間で使用する多項式は、隣接する区間との接続点で微分係数が一致するように選ばれる。これにより、全体として滑らかな曲線が得られる。
スプライン補間法には、いくつかの種類がある。代表的なものとしては、以下がある。
・線形スプライン補間:各区間を直線で繋ぎます。最も単純なスプライン補間であるが、曲線の滑らかさは保証されない。
・2次スプライン補間:各区間を2次関数で繋ぐ。線形スプライン補間よりも滑らかな曲線が得られるが、曲率の連続性は保証されない。
・3次スプライン補間: 各区間を3次関数で繋ぐ。滑らかさと曲率の連続性が保証され、最も一般的に用いられる。
スプライン補間では、データ点 \((x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n)\)を結ぶ関数を複数の低次関数(通常は3次関数)で構成する。区間ごとに異なる関数\(S_i(x)\)を定義し、全体として 滑らかに接続されるようにする。$$S_i(x) = a_i + b_i(x - x_i) + c_i(x - x_i)^2 + d_i(x - x_i)^3$$各区間\([x_i, x_{i+1}]\)に対して、別々の3次関数を使う。
3次スプライン補間\(S_i(x)\)では、以下の条件を満たすように係数を決定する。
・補間条件(データ点を通る)$$S_i(x_i) = y_i, \quad S_i(x_{i+1}) = y_{i+1}$$
・連続性条件(隣接する区間で関数がつながる)$$S_i(x_{i+1}) = S_{i+1}(x_{i+1})$$
・1次微分の連続性$$S_i'(x_{i+1}) = S_{i+1}'(x_{i+1})$$
・2次微分の連続性$$S_i''(x_{i+1}) = S_{i+1}''(x_{i+1})$$
・境界条件
自然スプラインの場合$$ S_0''(x_0) = 0, \quad S_{n-1}''(x_n) = 0$$
固定端スプラインの場合$$S_0'(x_0) = f'(x_0), \quad S_{n-1}'(x_n) = f'(x_n)$$
周期スプラインの場合$$S_0'(x_0) = S_{n-1}'(x_n), \quad S_0''(x_0) = S_{n-1}''(x_n)$$
スプライン補間の利点は、滑らかな補間が可能(1次&2次微分が連続)、ラグランジュ補間より振動が少ない、計算が安定しやすい(高次多項式に比べて精度が良い)などであり、欠点は、計算コストが高い(連立方程式を解く必要がある)、追加点があると全体を再計算する必要がある、近似誤差が増えると、元のデータより不正確な曲線になることがある、などがある。スプライン補間法は、低次の多項式を区間ごとにつなぐ補間手法であり、高次の多項式補間に比べて滑らかで安定した補間が可能である。
Scilabによるスプライン補間のスクリプト例を示す。(自然スプラインの例)
//スプライン補間
clear;clf;
// データ点
x = [-1.0, 0, 1.3, 2.0, 3.4, 4.0]; // x座標
y = [0.2, 1.0, 0.4, 1.6, 0.2, 1.3]; // y座標
// スプライン補間
spline_result = splin(x, y, "natural");
// 補間曲線を滑らかにするための x の値
x_interp = linspace(min(x), max(x), 100);
// 補間曲線の計算
y_interp = interp(x_interp, x, y, spline_result);
// グラフの描画
plot(x, y, 'o', x_interp, y_interp, '-');
xlabel("x");
ylabel("y");
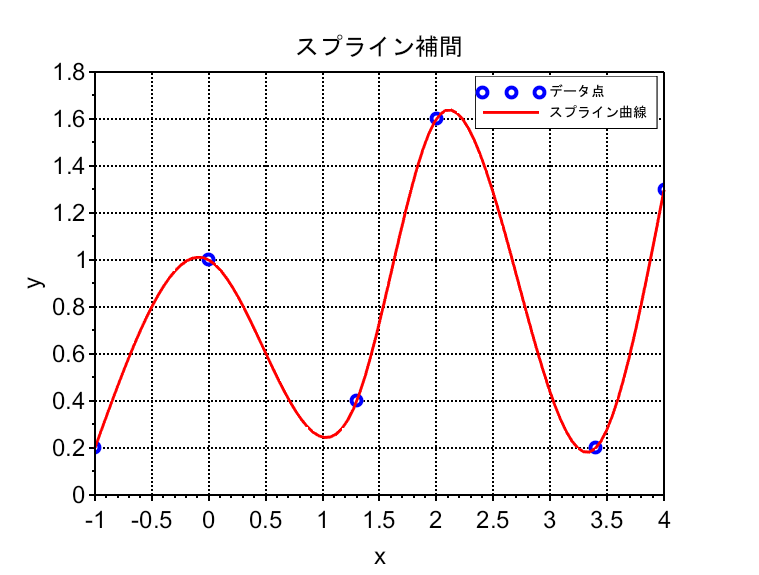
title("スプライン補間");
legend("データ点", "スプライン曲線");