8-2. 回帰分析と相関
回帰分析
回帰分析は、ある変数(目的変数)の変動を、他の変数(説明変数)との関係を通じて説明・予測するための統計手法である。計測工学では、センサデータの解析や測定精度の向上、システムの最適化を目的として回帰分析が活用される。具体的には、以下がある。
・センサデータの補正と校正
センサによる測定データには誤差やノイズが含まれることが多いため、回帰分析を用いることでデータの補正や校正が可能になる。例えば、「温度センサの出力と実際の温度の関係を回帰分析し、測定誤差を補正する。」「ひずみゲージの出力と荷重の関係を分析し、精度の高い荷重測定モデルを構築する。」などがある。
・測定値と環境要因の関係性の解析
測定値は、温度・湿度・圧力・振動などの環境要因によって影響を受けることが多いため、回帰分析を用いて影響を定量的に評価できる。例えば、「測定器の出力が温度変化によってどの程度ずれるかを分析し、補正モデルを作成する。」「電圧計の測定誤差が湿度に依存する場合、その関係を回帰分析で特定し、補正係数を求める。」などがある。
・複数センサの統合
複数のセンサを組み合わせた計測システムでは、各センサのデータを統合するために回帰分析が使われる。例えば、「カメラ、加速度計、ジャイロセンサを統合し、より正確な物体の動きを推定する。」「圧力センサと流量センサのデータを統合し、流体の特性をより精度よく測定する。」などがある。
・数学モデルの構築
実験データから測定システムの特性を記述する数学モデルを導出する際にも回帰分析が利用される。例えば、「材料の強度と応力の関係を回帰分析し、強度予測式を作成する。」「モーターの電流と回転数の関係を分析し、最適な制御モデルを構築する。」などがある。
・故障予測と異常検知
回帰分析を活用して、測定機器やセンサの異常を早期に検知できる。例えば、「温度センサの過去のデータと現在の測定値を比較し、異常なドリフトを検出する。」「計測機器の劣化に伴う測定誤差の傾向を回帰分析し、故障予測モデルを構築する。」などがある。
線形回帰分析
線形回帰分析は、統計学において、予測する変数(目的変数:従属変数)を予測するために用いる変数(説明変数:独立変数)を使って予測したり、2つの変数の間の関係性を明らかにしたりするために用いられる最も基本的な手法の一つである。
線形回帰分析では、目的変数と説明変数の間に線形の関係があることを仮定する。
単回帰モデルは、式(1)で表す。$$y=ax+b+\epsilon \;\;\;\cdots (1)$$ここで、\(y\): 目的変数、\(x\): 説明変数、\(a\): 回帰係数(傾き)、\(b\): 切片、\(\epsilon\): 誤差項である。
式(1)は、\(y\)が\(x\)に比例する関係にあることを表している。\(a\)は\(x\)が 1 単位変化したときに\(y\)がどれだけ変化するかを表し、\(b\)は\(x\)が\(0\)のときの\(y\)の値を表す。\(\epsilon\)は、モデルでは説明できない\(y\)の変動を表す。実際のデータを用いて、モデルのパラメータ(\(a,\;b\))を推定するが、最も一般的な方法として、最小二乗法を使う。最小二乗法では、実際のデータとモデルによる予測値との差の二乗和を最小にするように、パラメータを決定する。
重回帰分析は、2つ以上の説明変数 \(x_1, x_2, \dots, x_p\) を用いて目的変数\(y\)を予測するモデル である。$$y = a_0 + a_1 x_1 + a_2 x_2 + \dots + a_p x_p + \epsilon$$ ここで、\(x_1,x_2,\ldots,x_p\)は複数の説明変数、\(a_1, a_2, \ldots, a_p\)はそれぞれの説明変数の影響度(回帰係数)である。
重回帰分析は、行列を用いて一般化できる。$$\mathbf{y} = \mathbf{X} \boldsymbol{a} + \boldsymbol{\epsilon}$$ここで、\(\mathbf{y}\) :\(n \times 1\)の目的変数ベクトル\(\mathbf{X}\) :\(n \times (p+1)\) の説明変数行列(最初の列は1で、切片 \(a_0\) に対応)、\(\boldsymbol{a}\) :\((p+1) \times 1\)の回帰係数ベクトル、\(\boldsymbol{\epsilon}\) :\(n \times 1\) の誤差ベクトルである。
最小二乗法による回帰係数の推定式は、$$\boldsymbol{a} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}$$となる。
線形回帰モデルを適用するには、以下の仮定を満たしていることが重要である。
・線形性:説明変数と目的変数の関係が線形であること。
・独立性:誤差項が互いに独立であること。
・等分散性:誤差項の分散が一定であること。
・非多重共線性:説明変数同士が強い相関を持たないこと(重回帰分析の場合)。
・正規性:誤差項が正規分布に従うこと。
これらの仮定が満たされない場合、モデルの信頼性が低下する可能性がある。
相関関係
相関とは、2つの変数がどの程度関連しているかを表す指標 である。例えば、身長と体重の関係や、広告費と売上の関係などが相関の例である。相関を分けると以下となる。
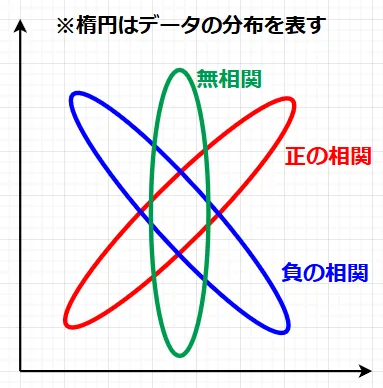
・正の相関:一方の変数が増えると、もう一方の変数も増加する関係。(例:人口とゴミの量)。
・負の相関:一方の変数が増えると、もう一方の変数が減少する関係。(例:平均気温と積雪量)。
・無相関:2つの変数に関連性が見られない関係。(例:身長と学力)。
相関の強さを定量的に示すために、相関係数が使われる。最も一般的な指標は ピアソンの相関係数 である。
ピアソンの相関係数\(r\)の定義は式(2)で定義される。$$r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2} \cdot \sqrt{\sum (y_i - \bar{y})^2}} =\frac{S_{xy}}{\sqrt{S_{xx} S_{yy}}}\;\;\; \cdots (2)$$ここで、\(\bar{x}, \bar{y}\):それぞれの変数の平均値、\(x_i, y_i\):それぞれの変数の観測値 、である。また、\(S_{xy}\)は共分散、\(\sqrt{S_{xx}},\; \sqrt{S_{yy}}\)は、それぞれ\(x\)の標準偏差、\(y\)の標準偏差である。\(S_{xy}^2 \leq S_{xx} S_{yy}\)なので、ピアソンの相関係数 \(r\) は、\(|r| \leq 1 \)の範囲となる。
| \(r\) の値 | 相関の強さ | 備考 |
|---|---|---|
| \(r = 1\) | 完全な正の相関 | \(x\) が増えると\(y\) も必ず増える |
| \(0.7 \leq r < 1\) | 強い正の相関 | かなり強い関係がある |
| \(0.3 \leq r < 0.7\) | 中程度の正の相関 | 一定の関係はあるが、外れ値もある可能性 |
| \(0 < r < 0.3\) | 弱い正の相関 | 関係性はあるが、影響は小さい |
| \(r = 0\) | 無相関 | 変数間に関係性がない |
| \(-0.3 < r < 0\) | 弱い負の相関 | 少し関係性があるが、影響は小さい |
| \(-0.7 < r \leq -0.3\) | 中程度の負の相関 | 一定の負の関係性がある |
| \(-1 < r \leq -0.7\) | 強い負の相関 | かなり強い負の関係がある |
| \(r = -1\) | 完全な負の相関 | \(x\)が増えると\(y\)が必ず減る |
相関と因果関係の違い
相関があるからといって、因果関係があるとは限らない ことに注意が必要である。例えば、以下のような関係は相関があるものの、因果関係はない可能性が高い。
[例] アイスクリームの売上と水難事故の発生件数 → 夏に増えるが、直接の関係はない(気温という共通要因がある)。
擬似相関として、2つの変数が無関係なのに、たまたま相関が高くなることがある。この場合は、共通の第三要因が影響を与えている場合 が多い。
ただし、因果関係があれば、相関係数が高いというのは正しい。
分散分析
分散分析は、3つ以上のグループ間の平均値に統計的な差があるかどうかを検証するために用いられる統計学的な手法である。
分散分析の主な目的は、グループ間の違いが偶然か、それとも統計的に有意なものかを判断することにある。例えば、「3種類の肥料(A, B, C)を使ったときの植物の成長量に違いがあるか?」、「3つの異なる教え方(A, B, C)によって生徒の成績に差が出るか?」、このような場合に、分散分析を使って「どのグループの平均値に差があるか」を検定する。
分散分析では、データのばらつきを 「グループ間の変動」 と 「グループ内の変動」 に分解して比較する。
総変動=「グループ間の変動」 +「グループ内の変動」
グループ間の変動は、各グループの平均値の違いによる変動であり、グループ内の変動は、各グループのデータのばらつき(個人差や誤差)による変動である。
もしグループ間の変動が大きく、グループ内の変動よりも統計的に有意に大きければ、「グループごとに平均値に差がある」と判断できる。
分散分析には、様々な種類がある。
・一元配置分散分析:1つの要因(独立変数)によってグループ分けされたデータを分析する場合に用いられる。
・二元配置分散分析: 2つの要因によってグループ分けされたデータを分析する場合に用いられる。
・多変量分散分析:複数の目的変数がある場合に用いられる。
分散分析の前提条件は、以下である。これらの条件を確認してから進めることが重要である。
・正規性:各グループのデータが正規分布に従っていること。
・等分散性:各グループの分散が等しいこと。
・独立性:各観測値が独立していること。
また、各グループのサンプルサイズが十分に大きいことが望ましい。
分散分析では、次の仮説を検定する。
帰無仮説(\(H_0\)):すべてのグループの平均値は等しい。 $$H_0: \mu_1 = \mu_2 = \dots = \mu_k$$
対立仮説(\(H_1\)):少なくとも1つのグループの平均値が異なる。
一元配置分散分析は、1つの要因(独立変数)に対して、複数の水準(グループ)を比較する方法 で、モデルは式(3)で表せる。$$y_{ij} = \mu + \alpha_i + \epsilon_{ij} \;\;\; \cdots (3)$$ここで、\(y_{ij}\) :\(i\) 番目のグループの \(j\)番目の観測値、\(\mu\) :全体の平均(母平均)、\(\alpha_i\) :グループ\(i\) の効果(グループ間の差)、\(\epsilon_{ij}\) :誤差(グループ内の個人差や測定誤差)である。
分散分析では、「F値(F統計量)」を計算し、それが有意かどうかを検定する。$$F = \frac{\text{グループ間の分散}}{\text{グループ内の分散}} = \frac{\text{MSB}}{\text{MSW}}$$ここで、MSB:グループ間の変動の平均、MSW:グループ内の変動の平均、である。
F値が大きいほど、グループ間の差が有意である可能性が高い。
F 値が有意水準よりも大きければ、帰無仮説を棄却し、対立仮説(グループ間に差があると判断)を採択することになる。
二元配置分散分析:一元配置分散分析では 1つの要因 だけを比較したが、二元配置分散分析では 2つの要因 を同時に考慮する。例えば、「肥料(A, B, C)」と「日照条件(短・長)」が植物の成長に与える影響 を同時に分析や、「教育方法(A, B, C)」と「学年(小4, 小5, 小6)」がテスト成績に与える影響 を分析、などである。

