8-3. 測定値の分散分析
統計的な1つのデータの集団を母集団というが、調査対象とする2つ以上の母集団の間に互いに差があるか、どの程度の差があるかを検討するのに分散分析法を使う。
要因と水準
要因:出力変数または応答変数(実験結果)の大きさを評価するための入力(変動)する変数で、因子ともいう。温度、圧力、電流などが因子となる。
水準:因子の影響をみるため、その大きさを何段階かに変えるときの段階のこと。例えば、温度が因子\(C\)とすると、\(C_1 = 30 \)[℃]、\(C_2=50\)[℃]、\(C_3=70\)[℃]は3水準である。
いくつかの要因によって測定値が変動するとき、各因子の水準が異なることにより生じた部分と、誤差により生じた部分を分解して、比較検討することを分散分析という。ここでの誤差は、偶然誤差と測定器の傾向的な系統誤差である。
| 水準 | 1 | 2 | \(k\) | 合計 |
| 測定回数 1 | \(x_{11}\) | \(x_{21}\) | \(x_{k1}\) | |
| 2 | \(x_{12}\) | \(x_{22}\) | \(x_{k2}\) | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | |
| \(n_i\) | \(x_{1n1}\) | \(x_{2n2}\) | \(x_{knk}\) | \(N=n_1+ \cdots+ n_k\) |
| 縦列和 | \(T_1\) | \(T_2\) | \(T_k\) | \(T\)(総和) |
| 縦列平均 | \(\bar{x_1}\) | \(\bar{x_2}\) | \(\bar{x_k}\) | \(\tilde{x}\)(総平均) |
| 2乗和 | \(T_1^2\) | \(T_2^2\) | \(T_k^2\) | \(\sum{T_i^2}\) |
| \(\sum{x_{1j}^2}\) | \(\sum{x_{2j}^2}\) | \(\sum{x_{kj}^2}\) | \(\sum{\sum{x_{ij}^2}}\) |
\(k\):水準の数、\(n_i\):各水準毎の変量の数、\(N\):全変量の数(\(N=\sum{n_i}\))、\(T_i\):縦列毎の変量の和、\(T_i/n_i\):水準\(i\)の変量の平均値\(\bar{x_i}\)、\(T\):全変量の総和、\(T/N\):総平均\(\tilde{x}\)
独立な水準を\(k\)個として、\(i\)番目の水準には\(n_i\)個の標本(測定値)がある。この各標本集団を縦に並べたものが表1である。表1で、縦列和とその総和、縦列平均とその総平均、縦列和の2乗とその総和、縦列データ毎の二乗の和とその総和などを求めると、式(1)が求まる。$$\sum_i{\sum_j{(x_{ij} - \tilde{x})^2}}=\sum_i{n_i(\bar{x_i}-\tilde{x})^2} + \sum_i{\sum_j{(x_{ij} - \bar{x_i})^2}} \;\;\; \cdots (1)$$
測定値:\(x_{ij}\)、 各機器番号\(i \leq k\)、\(j(=1,\ldots , n_i)\)は同一機器からのサンプル
平均値:\(\tilde{x}\)(全平均値)、\(\bar{x_i}\)(\(k\)台ある機器毎の平均値)、全平均値は、すべての標本に機器(水準)間の差が無いと仮定した場合の中央値
全変動:全変動\(S_T\) = 群間変動\(S_B\) + 群内変動\(S_W\) これが、式(1)である。
群間変動:式(1)の右辺第1項で、水準毎の変化の総和で、偶然とは考えられない系統的な誤差の変動の程度を表す。
群内変動:式(1)の右辺第2項で、1水準内での繰り返し測定によるばらつきの総和で、偶然誤差の変動の程度を表す。
分散分析では、式(1)の右辺の2群の変動成分を比較して、$$\text{群内変動(偶然と考える)} << \text{群間変動(必然と考える)}$$ならば、群間変動は有意であるということを検定する。
一元配置法
測定値に変動を生じる要因が1種類と考えられるとき、表1の一元配置法を使う。
式(1)より、$$S_T = \sum_i{\sum_j{(x_{ij} - \tilde{x})^2}} \quad \text{(全変動)} \\ S_B = \sum_i{n_i(\bar{x_i} - \tilde{x})^2} \quad \text{(群間変動)} \\ S_W = \sum_i{\sum_j{(x_{ij} - \bar{x_i})^2}} \quad \text{(群内変動)}$$であり、$$S_T = S_B + S_W$$である。
自由度は、\(F\)分布数値表を引くときに使用する指標で、以下の式により求める。$$S_B \text{の自由度} \quad \phi_B = k-1 \quad \text{平均値が分かっているから1を引く} \\ S_W \text{の自由度} \quad \phi_W = N-k \\ S_T \text{の自由度} \quad \phi_T = N-1$$
不偏分散は、以下の式となる。
・要因の不偏分散 \(V_B=\frac{S_B}{\phi_B}\):誤差と要因効果からなる
・残差の不偏分散 \(V_W=\frac{S_W}{\phi_W}\):誤差成分
・不偏分散比 \(F_{N-k}^{k-1} = \frac{V_B}{V_W}=\text{(誤差+要因効果)/(誤差)}\)
F分布
\(F\)分布は、1つの母集団から抽出した2組のデータ群(標本)による分散比、または2つの母集団の分散比の検定に使われる。\(F\)分布は、2つの独立したカイ二乗分布(\(\chi^2\)分布)を自由度で割った比 によって定義される確率分布である。
ある母集団から2組の実験値を抽出し、平均を\(\bar{x},\;\bar{y}\)、不偏分散を\(\sigma_x^2,\; \sigma_y^2\)とするとき、\(F\)分布は、自由度を\(d_x,\;d_y\)として、式(2)で表される。$$F = \frac{\frac{\sigma_x^2}{d_x}}{\frac{\sigma_y^2}{d_y}} \;\;\; \cdots (2)$$F分布は、自由度(\(d_1,\;d_2\))によって形状が決まり、右に裾野を引く非対称な分布 になる。図1に例を示す。
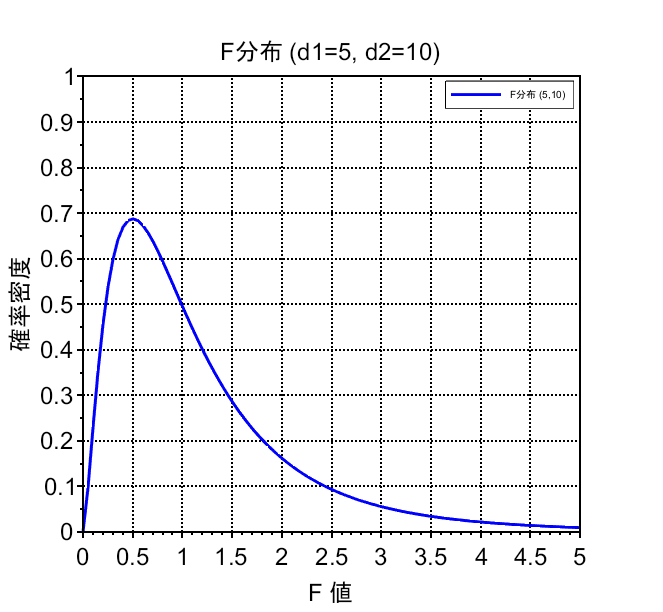
\(\chi^2\)分布
正規分布に従う確率変数の二乗和が従う確率分布 で、母分散の推定、独立性の検定(カイ二乗検定)、適合度検定などで広く使用 される。
カイ二乗分布は、\(k\) 個の独立した標準正規分布(平均0、分散1)に従う確率変数 \(Z_i\)の二乗和によって定義される。$$\chi^2 = Z_1^2 + Z_2^2 + \dots + Z_k^2$$ここで、\(Z_i\) は標準正規分布\(N(0,1)\) に従う独立な確率変数、\(k\)は 自由度である。自由度\(k\)によって、カイ二乗分布の形状が決まる。
カイ二乗分布には以下の特徴がある。
・ 非対称な分布であり、自由度が増えると正規分布に近づく
・ 確率変数は常に非負(\(\chi^2 \geq 0\))
・ 自由度 \(k\) によって分布の形が変わる
(1) 平均(期待値)と分散$$E[\chi^2] = k, \quad \text{Var}[\chi^2] = 2k$$(2) 大数の法則
自由度 \(k\)が大きくなると、カイ二乗分布は正規分布 に近づく。$$\frac{\chi^2 - k}{\sqrt{2k}} \to N(0,1) \quad (k \to \infty$$
\(F\)検定は、2つの標本(または母集団)間のばらつき、すなわち不偏分散(または母分散)に差があるかを統計的に検定する方法のうち、不偏分散比が\(F\)分布に従うような検定である。検定は、帰無仮説(2つの不偏分散に差が無い、不偏分散比\(F=1\))から出発し、計算の結果、「その仮説が間違いだった」として棄却する判断が生じる。その棄却判断の確率的基準を有意水準という。
群間変動\(S_B\)が大きいほど\(F\)値が大きくなり、要因の効果が大きくなる。要因効果が無い場合、各群の平均値の差が無く、\(F\)値は1に近づく。
\(F\)分布曲線の描画用Scilabスクリプト
// F分布図(自由度 d1 = 5, d2 = 10)
clf; clear;
//F分布の確率密度関数
function y = f_pdf(x, d1, d2)
num = gamma((d1+d2)/2)/(gamma(d1/2)gamma(d2/2));
num = num(d1/d2)^(d1/2);
denom = (1+(d1/d2)x).^((d1+d2)/2); y = num(x.^(d1/2-1))./denom;
endfunction
// パラメータ設定
d1 = 5; // 分子の自由度
d2 = 10; // 分母の自由度
// x軸の範囲設定(0から5まで100等分)
x = linspace(0,5,100);
// F分布の確率密度関数(PDF)の計算
y = f_pdf(x,d1,d2);
// グラフ描画
plot(x,y,"b","LineWidth",2);
xlabel("F 値");
ylabel("確率密度");
title("F分布 (d1=5, d2=10)");
legend("F分布 (5,10)", "upper right");
分散分析の評価
\(F\)分布曲線を使って、2つの標本間(または母集団)における不偏分散比の変動が有意であるかどうかを調べる。図1を参照。
・有意水準:検定で定めておくある確率\(\alpha\)。慣例により、\(\alpha\)を0.05(5%)や0.01(1%)にとる。これは小さい確率であるが、これが起これば母集団間に有意な差があったと認める。有意水準は危険率ともいい、危険率(いわゆる気まぐれの確率)が5%や1%ということは、\(\text{信頼度} = 100 \times (1-\alpha)\)[%]がそれぞれ、95%、99%ということになる。
・棄却領域:有意水準(危険率)\(\alpha\)を与える領域のこと。
・評価:分散分析表を作成し、不偏分散比\(F\)の値を求め、評価する。
1)\(F\)値が\(\alpha=0.05\)の値より大きい時、標本間(群間)の差が有意であるとする。\(F\)値が5%、または1%よりはるかに大きい場合は、要因の効果が確実である。
2)\(F\)値が\(\alpha=0.05\)から\(\alpha=0.01\)の間は、有意水準5%で有意差あり、と判定する。
3)\(F\)値が\(\alpha=0.05\)の値以下のとき、群間が均一か、5%以上の危険率をもって群間に差があるとする。
| 要因 | 変動 | 自由度 | 不偏分散 | 不偏分散比 |
| 群間変動 | \(S_B\) | \(\phi_B\) | \(V_B\) | \(F_{N-k}^{k-1}\) |
| 群内変動 | \(S_W\) | \(\phi_W\) | \(V_W\) | |
| 全変動 | \(S_T\) | \(\phi_T\) |
一元配置法の計算例
3水準で、標本が各5である試験データが表3のように得られた。これを分散分析により、評価する。
| 標本 | 1 | 2 | 3 | |
| 変量 1 | 8 | 10 | 12 | |
| 2 | 5 | 7 | 10 | |
| 3 | 7 | 9 | 8 | |
| 4 | 4 | 6 | 7 | |
| \(n_i=5\) 5 | 6 | 8 | 10 | \(N=5+5+5=15\) |
| 縦列和 | \(T_1=30\) | \(T_2 = 40\) | \(T_3 = 47\) | \(T=117\)(総和) |
| 縦列平均 | \(\bar{x_1}=6\) | \(\bar{x_2} = 8\) | \(\bar{x_3}=9.4\) | \(\tilde{x} = 7.8\)(総平均) |
1)残差の二乗和総計$$S_T = \sum_i{\sum_j{(x_{ij} - \tilde{x})^2}} =64$$
2)群間変動$$S_B = \sum_i{n_i(\bar{x_i} - \tilde{x})^2} =29$$
3)群内変動 残差の二乗和$$S_W = \sum_i{\sum_j{(x_{ij} - \bar{x_i})^2}} =35$$
4)\(S_B + S_W = 64\) なので、\(S_T = S_B +S_W\)
5)自由度$$S_B\text{の自由度} \phi_B = k -1 = 3-1=2 \\ S_W \text{の自由度} \phi_W = N-k=15-3 =12 \\ S_T\text{の自由度} \phi_T = N-1=15-1=14$$
6)不偏分散$$\text{要因の不偏分散} V_B=\frac{S_B}{\phi_B}=14.5 \\ \text{残差の不偏分散}V_W = \frac{S_W}{\phi_W}=2.92 \\ \text{不偏分散比}F_{N-k}^{k-1} =\frac{V_B}{V_W}=4.97$$
自由度\(\phi_W = 12\)、\(\phi_B=2\)における\(F\)分布曲線を描き、\(\alpha=0.01\)のとき\(F=6.93\)、\(\alpha=0.05\)のとき\(F=3.89\)を読み取る。この実験データでの\(F=4.97\)は、\(alpha\)が0.05(5%)から0.01(1%)の範囲に入っているので、「有意水準5%で、群間の不偏分散は群内の不偏分散に対して有意差が認められる。」と判定できる。

