8-4. 2次形式表現での最小二乗法

２次形式表現を用いることで、最小二乗法をより簡潔に表現し、計算を効率化することができる。２次形式を利用した最小二乗法は、機械学習や統計モデル、時系列分析、信号処理など幅広い分野で応用されている。ここでは、その表現形式とScilabによる実装を紹介する。

最小二乗法は、観測データに対して最適なモデルをフィットさせるための方法で、誤差の二乗和を最小化することでパラメータを推定する。特に、線形回帰のような問題で広く使われる。
基本的な最小二乗法は、次の形で表される線形モデルを考える。$$y = X\beta + \varepsilon$$ここで、\(y\) は観測データのベクトル（\(n \times 1\)）、\(X\) は設計行列（\(n \times p\)）、\(\beta\) は未知のパラメータベクトル（\(p \times 1\)）、\(\varepsilon\) は誤差ベクトル（\(n \times 1\)）である。
※\(X\)入力データ、\(y\)出力データとか、\(X\)独立変数、\(y\)従属変数とか、分野によりその表現は様々である。
最小二乗法では、残差ベクトル \(\varepsilon\)のノルムの二乗を最小化することで、パラメータ \(\beta\)を求める。$$\min_{\beta} \| y - X\beta \|^2$$

２次形式を用いると、最小二乗法の目的関数は式(1)のように書き換えられる。$$\min_{\beta} (y - X\beta)^T (y - X\beta)\;\;\; \cdots (1)$$この式を展開すると$$y^T y - 2\beta^T X^T y + \beta^T X^T X \beta$$となる。この式は、\(\beta\)に関する2次形式の関数となっており、以下のように書ける。$$Q(\beta) = \beta^T A \beta + b^T \beta + c$$ここで、\(c = y^T y\)（定数項）、\(A = X^T X\)（正定値または半正定値行列）、\(b = -2 X^Ty\)である。
最適な \(\beta\)を求めるために、目的関数の勾配を計算し、ゼロと置く。$$\frac{\partial Q}{\partial \beta} = 2A\beta + b = 0$$これを解くと、通常の最小二乗推定量が得られる。$$\beta =-\frac{1}{2}A^{-1}b = (X^T X)^{-1} X^T y$$この解は、行列 \(X^T X\)が可逆（正則）である場合に存在する。もし \(X^T X\) が特異（非正則）ならば、擬似逆行列を用いて解を求めることもある。
この2次形式より、最小二乗法の問題は「2次関数の最小化問題」として扱える。この観点から、
・正定値行列 \(X^T X\) により、最小二乗推定量がユニークであるかが決まる。
・ヘッセ行列（Hessian） \(2X^T X\)が正定値であれば、目的関数は凸関数であり、最小値が一意に存在する。

２次形式の最小二乗法の数値例

以下の観測データをもとに、最小二乗法を使って係数 \(\beta\)を求める。

データセット$$X = \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ 1 & 4 \\ 1 & 5 \end{bmatrix}, \quad y = \begin{bmatrix} 2 \\ 2.8 \\ 3.6 \\ 4.5 \\ 5.1 \end{bmatrix}$$ここで、\( X\) は独立変数の行列であり、1列目はバイアス項（定数1）、2列目はデータの \(x\) 値である。
目的は、線形モデル$$y = \beta_0 + \beta_1 x + \varepsilon$$の係数 \(\beta_0\)（切片）と \(\beta_1\)​（傾き）を求めることである。
最小二乗法の解は以下の式で求まる。$$\beta = (X^T X)^{-1} X^T y$$
以下の計算ステップで求める。
１．\(X^T X\)を計算
２．\(X^T y\)を計算
３．逆行列 \((X^T X)^{-1}\)を計算
４．\(\beta\)を求める
計算結果：
$$X^T X = \begin{bmatrix} 5 & 15 \\ 15 & 55 \end{bmatrix} \\ X^T y = \begin{bmatrix} 18 \\ 61.9 \end{bmatrix} \\ (X^T X)^{-1} = \begin{bmatrix} 1.1 & -0.3 \\ -0.3 & 0.1 \end{bmatrix} \\ \beta = \begin{bmatrix} 1.23 \\ 0.79 \end{bmatrix}$$よって、求めた回帰式は$$y = 1.23 + 0.79x$$となる。

// Scilab スクリプト: 2次形式の最小二乗法
clc; clear;
// 観測データ
X = [1 1; 1 2; 1 3; 1 4; 1 5]; // 独立変数行列（バイアス項を含む）
y = [2; 2.8; 3.6; 4.5; 5.1]; // 従属変数ベクトル
// 最小二乗法の計算
XT = X'; // X の転置
XTX = XT * X; // X^T * X
XTy = XT * y; // X^T * y
beta = inv(XTX) * XTy; // (X^T X)^(-1) X^T y
// 結果を表示
disp("最小二乗推定値:");
disp(beta);
// プロット
x_vals = [0:0.1:8]'; // x 軸の値を生成
y_pred = beta(1) + beta(2) * x_vals; // 回帰直線
// グラフ描画
plot(X(:,2), y, 'ro'); // データ点（赤い丸）
plot(x_vals, y_pred, 'b-'); // 回帰直線（青線）
xlabel("x");
ylabel("y");
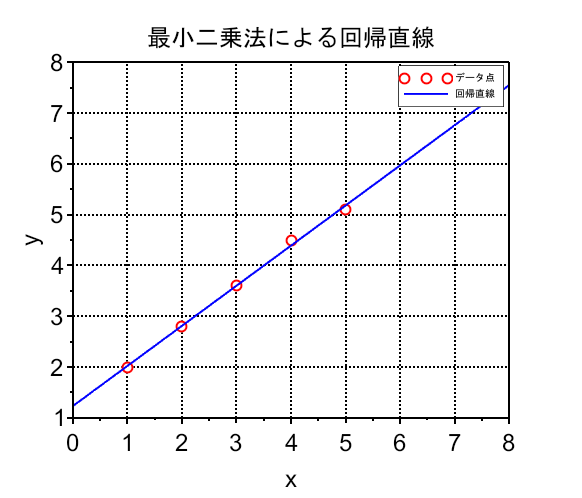
title("最小二乗法による回帰直線");
legend(["データ点", "回帰直線"]);
ーーーーーーーーーーーーーーーーーー

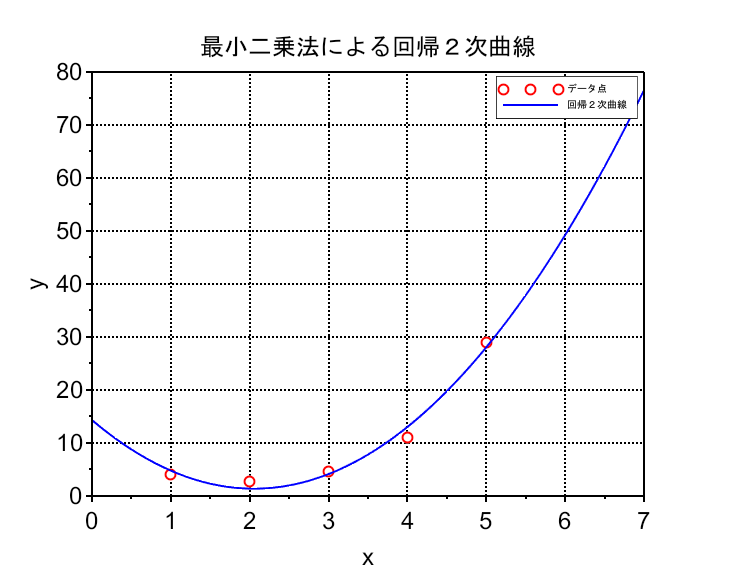
図２に2次曲線への最小２乗法の例を示す。
// Scilab スクリプト: 2次形式の最小二乗法
//２次曲線の場合
clc; clear;
// 観測データ
X = [1 1 1; 1 2 4; 1 3 9; 1 4 16; 1 5 25]; // 説明変数行列（バイアス項、１次項、２次項）
y = [4; 2.8; 4.6; 11; 29]; // 目的変数ベクトル
// 最小二乗法の計算
XT = X'; // X の転置
XTX = XT * X; // X^T * X
XTy = XT * y; // X^T * y
beta = inv(XTX) * XTy; // (X^T X)^(-1) X^T y
// 結果を表示
disp("最小二乗推定値:");
disp(beta);
// プロット
x_vals = [0:0.1:7]'; // x 軸の値を生成
y_pred = beta(1) + beta(2) * x_vals + beta(3) .* x_vals.^2; // 回帰2次曲線
// グラフ描画
plot(X(:,2), y, 'ro'); // データ点（赤い丸）
plot(x_vals, y_pred, 'b-'); // 回帰2次曲線（青線）
xlabel("x");
ylabel("y");
title("最小二乗法による回帰２次曲線");
legend(["データ点", "回帰２次曲線"]);