6. Z変換の演習

※\(\mathcal{Z}\)変換に関することは 2. Z変換法 を参照願います。

6-1. 指数関数の\(\mathcal{Z}\)変換

指数関数\(x(t) = e^{\alpha t},\; t \ge 0\) を周期\(T\)でサンプルして得た信号値系列を\(\mathcal{Z}\)変換せよ。

解答例： 周期\(T\)でサンプルして得た信号値系列は、\(e^0,\;e^{\alpha T},\; e^{2\alpha T},\; e^{3\alpha T},\ldots \)となる。従って、その\(\mathcal{Z}\)変換は、$$X(z) = 1 + e^{\alpha T}z^{-1} + e^{2\alpha T}z^{-2} + e^{3\alpha T}z^{-3} + \cdots$$となる。これは、無限等比級数なので、収束条件下（\(|z| \gt e^{\alpha T}\)）で、$$X(z) =\frac{1}{1 - e^{\alpha T}z^{-1}} = \frac{z}{z-e^{\alpha T}}$$である。

※Scilab で、サンプル値信号列をグラフにするスクリプトを示す。

6-2. 余弦波関数の\(\mathcal{Z}\)変換

余弦波関数\(x(t) = \cos \omega t,\; t \ge 0\) を周期\(T\)でサンプルして得た信号値系列を\(\mathcal{Z}\)変換せよ。

解答例： オイラーの公式より、\(e^{j \theta} = \cos \theta + j \sin \theta\)なので、$$\cos \omega t = \frac{1}{2}\left(e^{j\omega t} + e^{-j\omega t}\right)$$である。従って、周期\(T\)でサンプルして得た信号値系列は、$$x(kT) = \cos k\omega T = \frac{1}{2}\left(e^{jk\omega T} + e^{-jk\omega T}\right)$$となる。よって、その\(\mathcal{Z}\)変換は指数関数の\(\mathcal{Z}\)変換を利用して、$$X(z) = \frac{1}{2} \left(\frac{1}{1-e^{j \omega T}z^{-1}} + \frac{1}{1-e^{-j \omega T}z^{-1}}\right) \\ = \frac{1}{2}\left(\frac{z}{z-e^{j \omega T}} + \frac{z}{z - e^{-j \omega T}}\right) \\ = \frac{1}{2} \cdot \frac{2z^2 -z(e^{j\omega T} + e^{-j\omega T})}{z^2 -z(e^{j\omega T}+e^{-j \omega T})+1} = \frac{1}{2}\cdot \frac{2z^2 - 2z \cos \omega T}{z^2 -2z \cos \omega T + 1} \\= \frac{z^2 -z \cos \omega T}{z^2 - 2 z \cos \omega T +1}$$

6-3. ２次遅れ系の\(\mathcal{Z}\)変換

２次遅れ系のラプラス変換が式(1)で与えられている。周期\(T\)でサンプルして得た信号値系列を\(\mathcal{Z}\)変換せよ。$$X(s) = \frac{1}{s(s + 1)} \;\;\; \cdots (1)$$

解答例：　\(X(s)\)を部分分数展開すると、$$X(s) =\frac{1}{s(s + 1)} = \frac{1}{s} - \frac{1}{s+1}$$これを逆ラプラス変換すると、$$x(t)=I(t) - e^{-t}$$となる。ここで、\(I(t)\)は単位ステップ関数である。\(x(t)\)を周期\(T\)でサンプルして得られた信号値系列を\(\mathcal{Z}\)変換すると$$X(z)=\frac{z}{z-1} - \frac{z}{z- e^{-T}} = \frac{z(1-e^{-T})}{(z-1)(z-e^{-T})}$$となる。

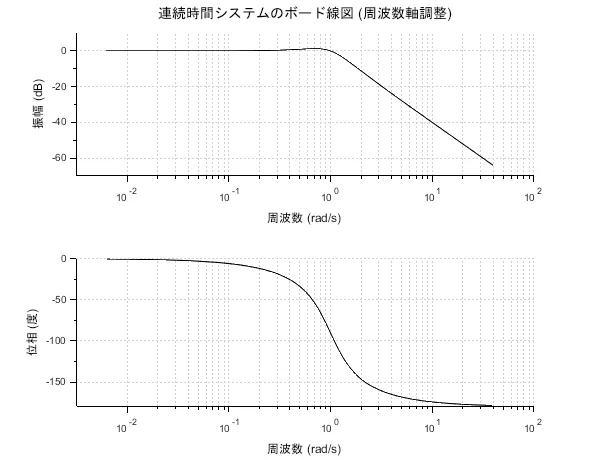
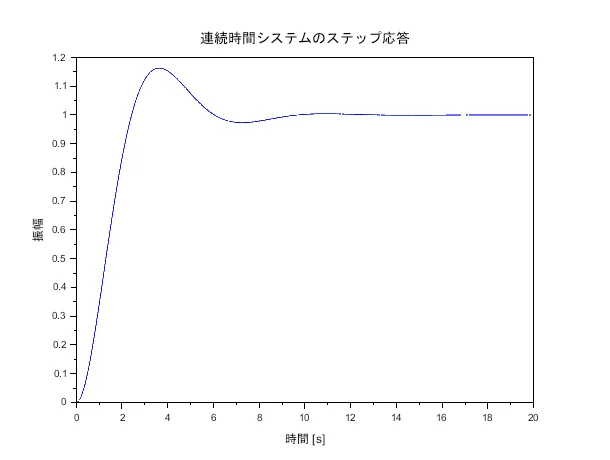
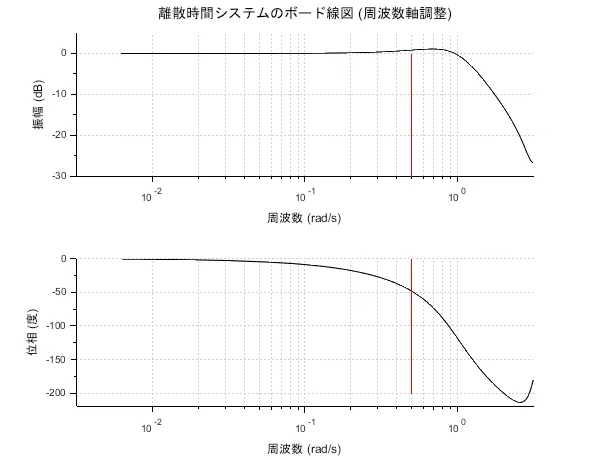
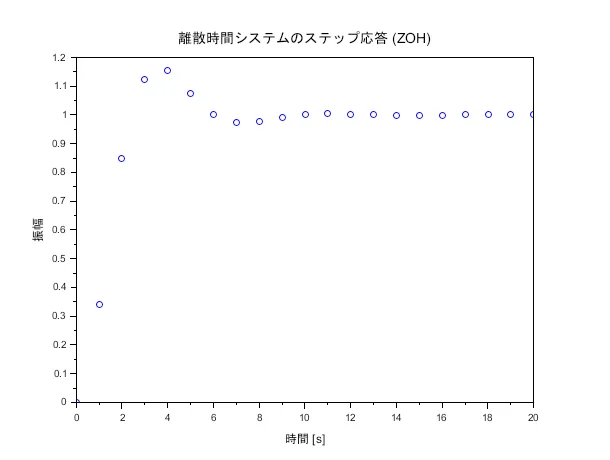
※Scilabによる2次遅れ系を離散化したシステムのボード線図、ステップ応答の描画スクリプトを示す。なお、離散化された伝達関数はPythonで得られた結果を利用している。
離散時間系のボード線図（図５）を見る上で注意点がある。離散時間系は有限な周波数範囲しか持てない（サンプリング定理）。サンプリング周期\(T\)によって、観測可能な周波数は次の範囲に制限される。$$\omega \in \left[0, \frac{\pi}{T}\right] \quad (\text{または} \, [0, \omega_s/2])$$ \(\omega_s = \frac{2\pi}{T}\) はサンプリング角周波数、\(\frac{\omega_s}{2}\)はナイキスト周波数である。

// Scilabスクリプト
// 2次遅れ系の離散化
clc; clear; clf();

// 連続時間システムの伝達関数
s = %s;
H_s = 1 / (s^2 + s + 1);

// パラメータ設定
T = 1.0;                  // サンプリング周期
t=0:0.001:20;             // 時間ベクトル (0〜20秒)
tz = 0:T:20;              // 離散時間

// 連続時間システムのステップ応答
H_ss = syslin('c', H_s);
y_c = csim('step', t, H_ss);

// ZOH を仮定した Z 変換 (Pythonによる離散化結果を利用)
//H_z = (0.00483342*z + 0.00467492) / (z^2 - 1.89532909*z + 0.90483742);
z = %z;
H_z = (0.34029985*z + 0.24168648)/(z^2  - 0.78589311*z + 0.36787944);
H_zs = syslin(T, H_z);

k = 1:length(tz);       // サンプリング点
r(k) = 1;              // ステップ入力
r = r';                // 列ベクトルに変換
y_d = flts(r, H_zs);   // 離散時間シミュレーション

// 周波数範囲の調整
w_min = 0.001;                         // 最小周波数 [rad/s]
w_max = %pi / T;　　　                  // 最大周波数

// ボード線図プロット
scf(0);
bode(H_ss, w_min, w_max, 'rad');       // 連続時間ボード線図
title("連続時間システムのボード線図 (周波数軸調整)");

scf(1);
bode(H_zs, w_min, w_max, 'rad');       // 離散時間ボード線図
title("離散時間システムのボード線図 (周波数軸調整)");

// ステップ応答プロット
scf(2);
plot(t, y_c);
xlabel('時間 [s]');
ylabel('振幅');
title('連続時間システムのステップ応答');

scf(3);
plot(tz, y_d, 'o');
xlabel('時間 [s]');
ylabel('振幅');
title('離散時間システムのステップ応答 (ZOH)');