11. 最小分散制御(1)
最小分散制御(Minimum Variance Control, MVC)は、システムの出力の分散を最小化することを目的とした制御手法である。これは、特にランダムな外乱やノイズの影響を受けるシステムに対して、できるだけ安定した出力を得るために用いられる。手法として、むだ時間分先の出力を予測し、その予測値に基づいて現時刻の操作量を決定する。この制御により、むだ時間を有するシステムに対して追従特性に優れた制御系を設計できるが、対象とするシステムにいくつかの厳しい前提条件を必要とする。
対象システムとして、式(1)の線形離散時間モデルで記述されるシステムを考える。$$A(q^{-1})y_k = q^{-j}B(q^{-1})u_k + C(q^{-1})e_k \;\;\; \cdots (1)$$ここで、\(y_k\)は出力信号、\(u_k\)は入力信号、\(e_k\)は平均値ゼロの白色雑音、\(q^{-1}\)はシフトオペレータ、である。また、\(A(q^{-1}),\; B(q^{-1}),\; C(q^{-1})\)は、以下で与えられる多項式である。$$A(q^{-1}) = 1 + a_1 q^{-1} + a_2 q^{-2} + \cdots + a_n q^{-n} \\ B(q^{-1}) = b_0 + b_1 q^{-1} + b_2 q^{-2} + \cdots + b_m q^{-m} \\ C(q^{-1}) = 1 + c_1 q^{-1} + c_2 q^{-2} + \cdots + c_l q^{-l} $$式(1)の両辺を\(A(q^{-1})\)で割ると、パルス伝達関数に相当する式(2)となる。ただし、\(\mathcal{Z}\)変換を施したのではなく、変数は時間関数のままである。$$y_k = \frac{B(q^{-1})}{A(q^{-1})}u_k q^{-j} + \frac{C(q^{-1})}{A(q^{-1})}e_k \;\;\; \cdots (2)$$ \(w_k\)を目標値として、式(3)の評価関数を導入する。$$J_1 = E\left[(y_{k+j} - w_{k+j})^2\right] \;\;\; \cdots (3)$$ 式(3)は制御偏差の分散を表している。これを最小にするのが、最小分散制御である。
11-1. 出力の予測
式(3)の評価関数\(J_1\)に含まれる\(y_{k+j}\)は、時刻\(k\)においては未知である。時刻\(k\)までの情報に基づいて予測せよ。
解答例: 式(3)の評価関数に含まれる\(y_{k+j}\)を時刻\(k\)までの情報に基づいて予測するためには、以下のように予測器を構成する。
1.式(1)の両辺に\(q^j\)を掛けて式(4)と書き換える。$$A(q^{-1})y_{k+j}=B(q^{−1})u_{k}+C(q^{−1})e_{k+j} \;\;\; \cdots(4)$$
2.多項式\(C(q^{-1})\)を\(A(q^{-1})\)で割って、商\(F(q^{-1})\)と余り\(G(q^{-1})\)を求める。$$C(q^{-1})=A(q^{-1})F(q^{-1})+q^{−j}G(q^{-1}) \;\;\; \cdots (5)$$ここで、$$F(q^{-1}) = 1 + f_1 q^{-1} + f_2 q^{-2} + \cdots + f_{j-1} q^{-(j-1)} \\ G(q^{-1}) = g_0 + g_1 q^{-1} + g_2 q^{-2} + \cdots + g_{n-1} q^{-(n-1)} $$である。
3.式(4)の両辺を\(A(q^{-1})\)で割って、式(5)を代入すると、$$y_{k+j}=\frac{B(q^{-1})}{A(q^{-1})}u_{k}+F(q^{-1})e_{k+j}+\frac{G(q^{-1})}{A(q^{-1})}e_k \;\;\; \cdots(6)$$
4.式(6)の両辺に\(A(q^{-1})\)を掛けると、$$A(q^{-1})y_{k+j} = B(q^{-1})u_{k}+G(q^{-1})e_k+A(q^{-1})F(q^{-1})e_{k+j} \;\;\; \cdots (7)$$式(7)において、時刻\(k\)までの情報に基づいて予測可能な項と、時刻\(k\)以降の情報が必要な項に分ける。
・予測可能な項: \(B(q^{-1})u_{k}\)、\(G(q^{-1})e_k\)
・予測不可能な項: \(A(q^{-1})F(q^{-1})e_{k+j}\) この項は、未来の白色雑音からなっているので、予測可能な項とは無相関である。
従って、時刻\(k\)における\(y_{k+j}\)の予測値\(\hat{y}_{k+j|k}\)は、以下のように与えられる。$$\hat{y}_{k+j∣k} = \frac{B(q^{-1})}{A(q^{-1})}u_{k} + \frac{G(q^{-1})}{A(q^{-1})}e_k \;\;\; \cdots (8)$$ここで、\(e_k\)は観測できないため、代わりに予測誤差\(\hat{e}_k\)を用いる。$$\hat{y}_{k+j∣k} = \frac{B(q^{-1})}{A(q^{-1})}u_{k} + \frac{G(q^{-1})}{A(q^{-1})} \hat{e}_k \;\;\; \cdots (9)$$予測誤差\(\hat{e}_k\)は、$$\hat{e}_k = y_{k} − \hat{y}_{k∣k−1} \;\;\; \cdots (10)$$ここで、\(\hat{y}_{k|k-1}\)は、時刻\(k-1\)における\(y_k\)の予測値である。なお、予測器の性能は、多項式\(A(q^{-1})\)、\(B(q^{-1})\)、\(C(q^{-1})\)の正確さに依存する。
11-2. 最小分散制御の制御則
式(3)の評価関数を最小にする制御則を求めよ。
解答例: 式(3)の評価関数\(J_1\)に式(9)を代入する。$$J_1 = E\left[(\hat{y}_{k+j|k} - w_{k+j})^2 \right]$$評価関数\(J_1\)を最小にするためには、\(\hat{y}_{k+j|k}=w_{k+j}\)となるように制御入力\(u_{k}\)を決定する。
式(9)を代入して\(u_{k}\)について解く。$$\frac{B(q^{-1})}{A(q^{-1})} u_{k} + \frac{G(q^{-1})}{A(q^{-1})}\hat{e}_k = w_{k+j} \\ B(q^{-1})u_{k} = A(q^{-1})w_{k+j} - G(q^{-1}) \hat{e}_k \\ u_{k} = \frac{A(q^{-1})}{B(q^{-1})}w_{k+j} - \frac{G(q^{-1})}{B(q^{-1})} \hat{e}_k \;\;\; \cdots (11)$$これを展開すると、$$u_{k} = \frac{A(q^{-1})}{B(q^{-1})}w_{k+j} - \frac{G(q^{-1})}{B(q^{-1})}(y_k - \hat{y}_{k|k-1})$$となる。これが評価関数\(J_1\)を最小にする制御則である。
制御則の第1項は、目標値\(w_{k+j}\)に追従するための項である。また、制御則の第2項は、予測誤差\(\hat{e}_k\)を補償するための項である。
Pythonによるシミュレーション例
以下のシステムを考える。$$A(q^{-1})=1−0.4q^{-1}, \quad B(q^{-1})=1+0.2q^{-1} ,\quad C(q^{-1})=1,\quad j=1$$このとき、式(5)より、$$F(q^{-1})=1,\quad G(q^{-1})=0.4$$となる。したがって、式(9)より、$$\hat{y}_{k+1} = \frac{1+0.2q^{-1}}{1-0.4q^{-1}}u_k + \frac{0.4}{1-0.4q^{-1}}\hat{e}_k$$よって、$$\hat{y}_k = u_{k-1} + 0.2u_{k-2} + 0.4\hat{e}_{k-1} + 0.4\hat{y}_{k-1}$$となる。また、 予測誤差は、$$\hat{e}_k=y_k − \hat{y}_{k∣k−1}$$である。 制御則は、式(11)より、$$u_k = \frac{1-0.4q^{-1}}{1+0.2q^{-1}}w_{k+1} - \frac{0.4}{1+0.2q^{-1}}\hat{e}_k$$よって、$$u_k = w_{k+1} - 0.4w_k -0.4\hat{e}_k - 0.2u_{k-1}$$となる。
#Python スクリプト
import numpy as np
import matplotlib.pyplot as plt
# システムパラメータ (安定な領域に設定)
a0 = 1
a1 = -0.4 # |a1| < 1 が安定条件
b0 = 1
b1 = 0.2
c1 = 0
g0 = 0.4
j = 1
# Simulation parameters
N = 200 # Number of simulation steps
w = np.ones(N) # Target value (step input)
y = np.zeros(N) # System output
y_hat = np.zeros(N) # Predicted output
e_hat = np.zeros(N) # Prediction error
u = np.zeros(N) # Control input
# Noise settings
noise_std = 0.05 # Standard deviation of white noise
noise = np.random.normal(0, noise_std, N) # Generate white noise
# Initial conditions
y[0] = 0
y[1] = 0
y_hat[0] = 0
y_hat[1] = 0
u[0] = 0
u[1] = 0
e_hat[0] = 0
e_hat[1] = 0
# Simulation loop
for k in range(2, N-1): # Start from k = 2 because of u_{k-2} dependency
# Compute control input using the given control law
u[k] = (w[k+1] + a1 * w[k] - g0 * e_hat[k] - b1 * u[k-1])/b0
# Compute predicted output using the predictor equation
y_hat[k] = (u[k-1] + b1 * u[k-2] + g0 * e_hat[k-1] - a1 * y_hat[k-1])/a0
# Simulate actual system output (includes noise)
y[k] = y_hat[k] + noise[k]
# Compute prediction error
e_hat[k] = y[k] - y_hat[k]
# Plot results
plt.figure(figsize=(10, 5))
plt.plot(range(N//2), w[:N//2], 'k--', label='w (Target Value)')
plt.plot(range(N//2), y[:N//2], 'b', label='y (System Output)')
plt.plot(range(N//2), u[:N//2], 'r', label='u (Control Input)')
plt.xlabel('Time Step')
plt.ylabel('Signal Value')
plt.title('System Output and Control Input with White Noise')
plt.legend()
plt.grid()
plt.show()
plt.figure(figsize=(10, 5))
plt.plot(range(N//2), w[:N//2], 'k--', label='w (Target Value)')
plt.plot(range(N//2), y_hat[:N//2], 'g', label='ŷ (PredictedOutput)')
plt.plot(range(N//2), e_hat[:N//2], 'r', label='e (prediction error)')
plt.xlabel('Time Step')
plt.ylabel('Signal Value')
plt.title('System Output and Control Input with White Noise')
plt.legend()
plt.grid()
plt.show()
※白色雑音が無い場合
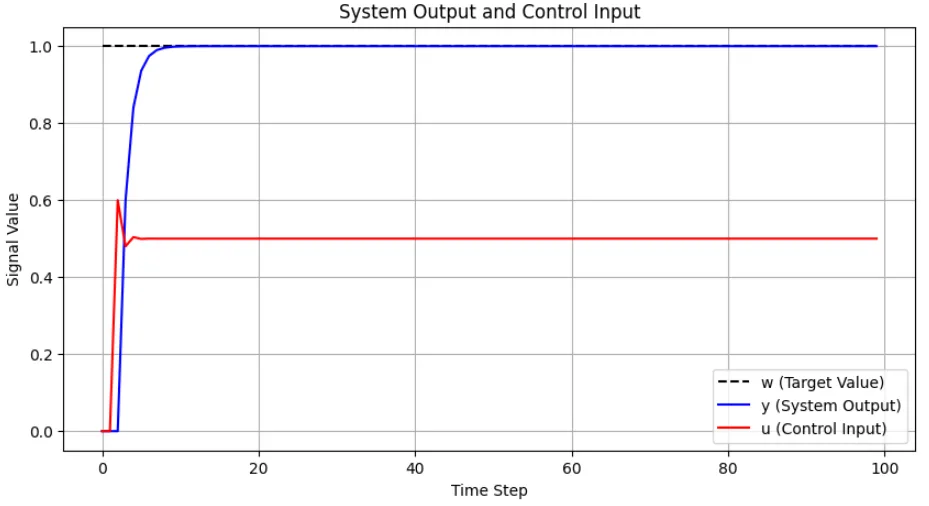
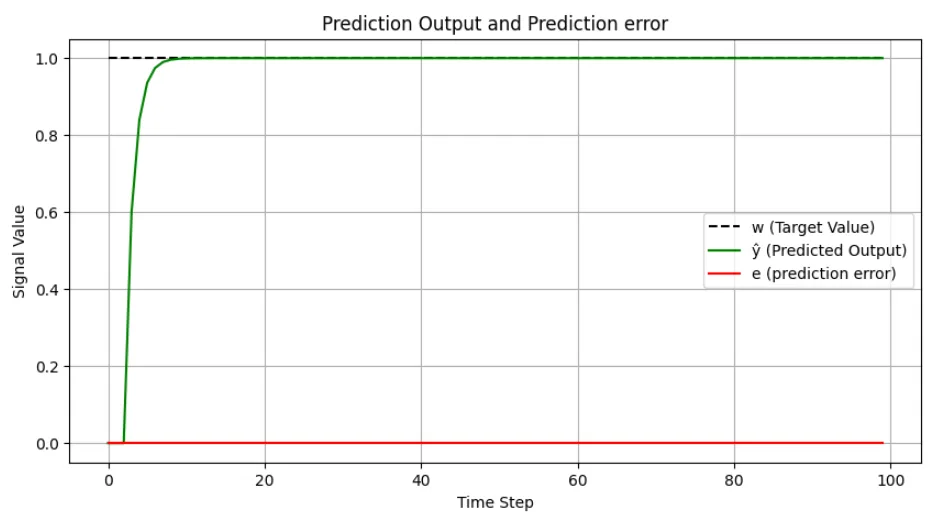
※白色雑音がある場合
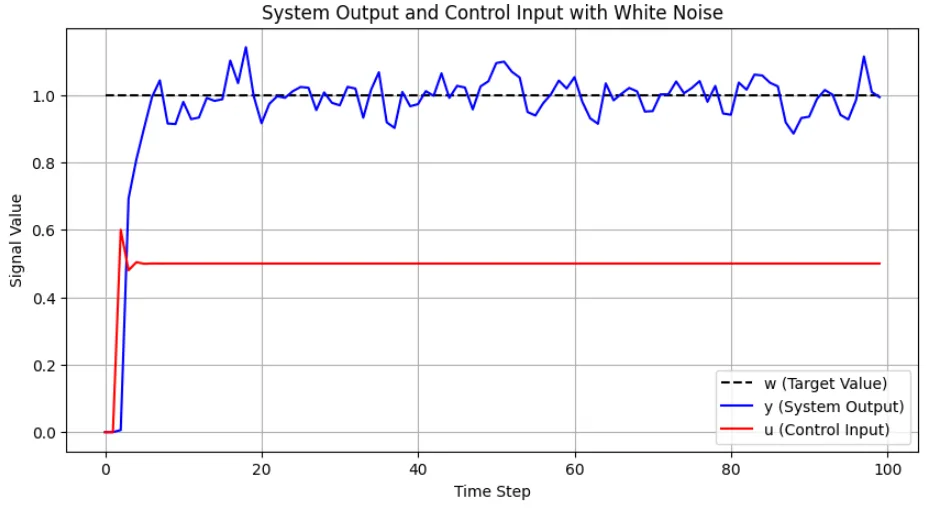
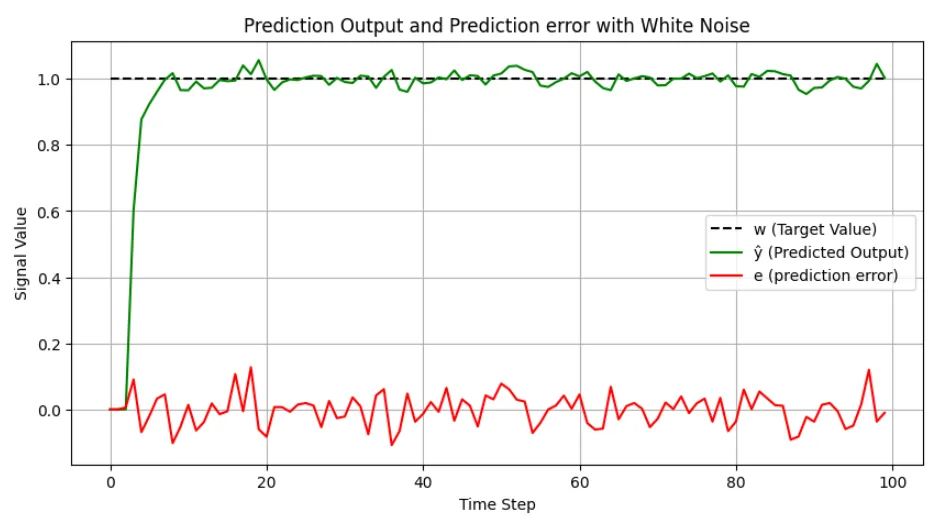


“11. 最小分散制御(1)” に対して1件のコメントがあります。
コメントは受け付けていません。