12. 最小分散制御（２）

※最小分散制御(1)の内容を再整理する。数式表現が異なるが、こちらの方が分かりやすいと思う。

式(1)の線形離散時間モデルで記述されるシステムを考える。$$A(q^{-1})y_k = q^{-j}B(q^{-1})u_k + C(q^{-1})e_k \;\;\; \cdots (1)$$ここで、\(y_k\)は出力信号、\(u_k\)は入力信号、\(e_k\)は平均値ゼロの白色雑音、\(q^{-1}\)はシフトオペレータ、である。\(A(q^{-1}),\; B(q^{-1}),\; C(q^{-1})\)は、以下の多項式である。$$A(q^{-1}) = 1 + a_1 q^{-1} + a_2 q^{-2} + \cdots + a_n q^{-n} \\ B(q^{-1}) = b_0 + b_1 q^{-1} + b_2 q^{-2} + \cdots + b_m q^{-m} \\ C(q^{-1}) = 1 + c_1 q^{-1} + c_2 q^{-2} + \cdots + c_l q^{-l} $$評価関数は、$$J_1 = E\left[(y_{k+j} - w_{k+j})^2 \right]$$とする。$$C(q^{-1}) = A(q^{-1}) F(q^{-1}) + q^{-j}G(q^{-1}) \;\;\; \cdots (2)$$とする。ここで、$$F(q^{-1}) = 1 + f_1 q^{-1} + f_2 q^{-2} + \cdots + f_{j-1} q^{-(j-1)} \\ G(q^{-1}) = g_0 + g_1 q^{-1} + g_2 q^{-2} + \cdots + g_{n-1} q^{-n_1} ,\quad n_1 = \text{max}\{n-1, l-j\}$$である。
式(1)の両辺に\(q^{j} F(q^{-1})\)を掛ける。$$A(q^{-1})F(q^{-1})y_{k+j} = B(q^{-1})F(q^{-1})u_k + C(q^{-1})F(q^{-1})e_{k+j}$$式(2)を使うと、$$C(q^{-1})y_{k+j} = G(q^{-1})y_k + B(q^{-1})F(q^{-1})u_k + C(q^{-1})F(q^{-1})e_{k+j}$$よって、$$y_{k+j} = \frac{1}{C(q^{-1})} \left\{G(q^{-1})y_k + B(q^{-1})F(q^{-1})u_k\right\} + F(q^{-1})e_{k+j}$$となる。ここで、第２項の\(F(q^{-1})e_{k+j}\)は未来の白色雑音となり、第１項と無相関なので、\(y_{k+j}\)の最適予測値は、$$\hat{y}_{k+j|k}=\frac{1}{C(q^{-1})} \left\{G(q^{-1})y_k + B(q^{-1})F(q^{-1})u_k\right\}$$である。\(\hat{y}_{k+j|k}\)は、時刻\(k\)までの情報に基づく\(j\)ステップ最適予測値を表す。
$$y_{k+j} = \hat{y}_{k+j|k} + F(q^{-1})e_{k+j}$$なので、これを評価関数に代入すると、$$J_1 = E \left[\left\{\hat{y}_{k+j|k} + F(q^{-1})e_{k+j} - w_{k+j} \right\}^2 \right] \\ = E\left[(\hat{y}_{k+j|k} - w_{k+j})^2 \right] +2 E \left[(\hat{y}_{k+j|k} - w_{k+j})F(q^{-1})e_{k+j}\right] + E\left[\left\{F(q^{-1})e_{k+j}\right\}^2\right]$$ここで、未来に印可される白色雑音\(F(q^{-1})e_{k+j}\)と \(\hat{y}_{k+j|k}\)、\(w_{k+j}\)とは無相関なので第2項はゼロとなる。従って、$$J_1 = E\left[(\hat{y}_{k+j|k} - w_{k+j})^2 \right] + E\left[\left\{F(q^{-1})e_{k+j}\right\}^2\right]$$である。この評価関数を最小にする操作量\(u_k\)は、\(\hat{y}_{k+j|k} - w_{k+j}=0\)を満たすものである。よって、$$w_{k+j} = \frac{1}{C(q^{-1})} \left\{G(q^{-1})y_k + B(q^{-1})F(q^{-1})u_k\right\}$$となり、これを\(u_k\)について解くと、$$u_k = \frac{1}{B(q^{-1})F(q^{-1})}\left\{C(q^{-1})w_{k+j} - G(q^{-1})y_k\right\}$$となる。これが最小分散制御の操作量である。図１に最小分散制御系のブロック線図を示す。

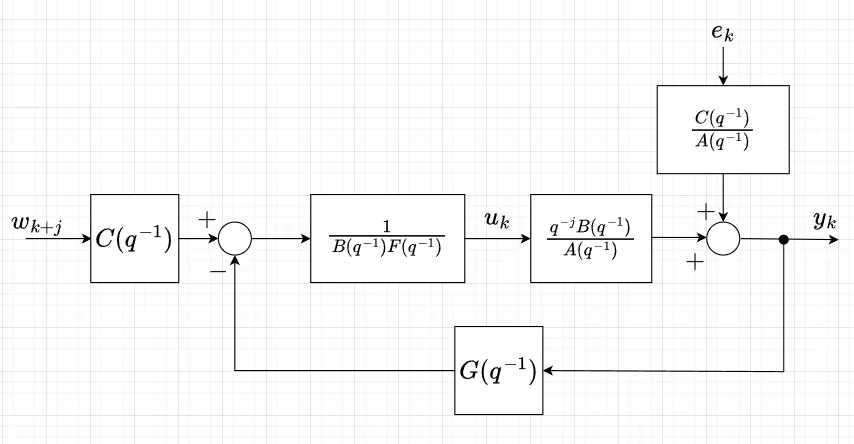
水位制御モデルの最小分散制御

式(1)で示すむだ時間を有する水位制御モデルをサンプリング周期\(T=3 \text{[s]}\)で離散化して最小分散制御を適用せよ。$$G(s) = \frac{30}{25.04 s^3 + 78.84 s^2 + 41.1 s +1}e^{-9s} \;\;\; \cdots (1)$$

解答例：　式(1)の伝達関数をゼロホールド (ZOH)を仮定して、離散化する。Pythonのcontrol ライブラリを用いると、ゼロホールド変換 (ZOH) による離散化を計算できる。

図２の実行結果より、むだ時間を除いた離散化後のシステムは$$A(q^{-1})=1−1.080q^{-1}+0.1426q^{-2}−7.855×10^{-5} q^{-3} \\ B(q^{-1})=0.9925+0.8683q^{-1}+0.01413q^{-2} $$である。サンプリング周期\(T=3\)なので、むだ時間のステップ数は\(j=3\)となり、 $$A(q^{-1}) y_k = q^{-3} B(q^{-1}) u_k$$と表せる。このシステムにはノイズの項がない。設計アルゴリズムで\(C(q^{-1})\)が必要なときは、\(C(q^{-1})=1\)とすればよい。式(2)より、$$1 = A(q^{-1})F(q^{-1}) + q^{-3}G(q^{-1})$$なので、$$A(q^{-1})=1−1.080q^{-1}+0.1426q^{-2}−7.855×10^{-5} q^{-3} \\ F(q^{-1}) = 1 + f_1 q^{-1} + f_2 q^{-2} \\ G(q^{-1}) = g_0 + g_1 q^{-1} + g_2 q^{-2}$$を代入展開し、係数を比較することで、$$F(q^{-1}) = 1 + 1.080q^{-1} +1.024q^{-2} \\G(q^{-1}) = 0.9519 - 0.1459q^{-1} + 8.043 \times 10^{-5} q^{-2}$$が求まる。
$$y_k = \frac{q^{-3}B(q^{-1})}{A(q^{-1})} \\ \hat{y}_{k+j|k}=\frac{1}{C(q^{-1})} \left\{G(q^{-1})y_k + B(q^{-1})F(q^{-1})u_k\right\} \\ u_k = \frac{1}{B(q^{-1})F(q^{-1})}\left\{C(q^{-1})w_{k+j} - G(q^{-1})y_k\right\}$$以上の結果より、シミュレーションを行う。

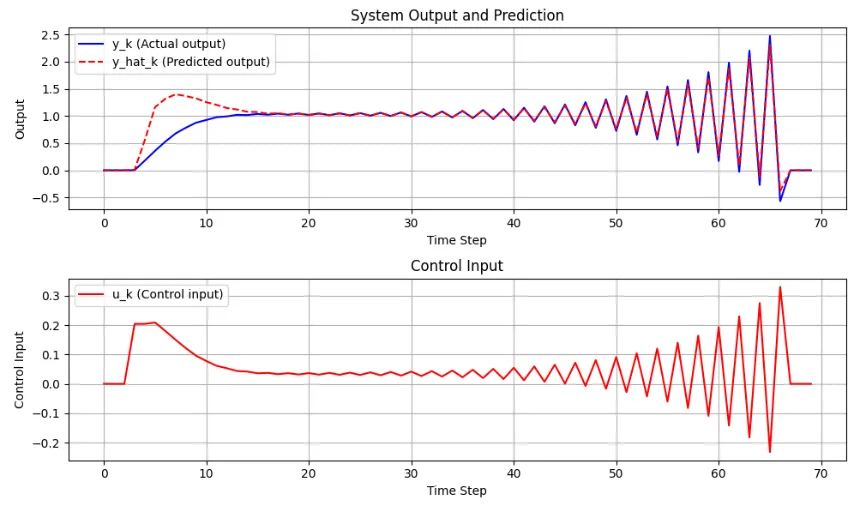
Pythonによるスクリプトとシミュレーション結果を示す。この制御系では制御器の極\(B(q^{-1})F(q^{-1})\)が不安定である。従って、シミュレーション結果は図３のように振動発散する。このようなシステムのシミュレーションの数値計算は難しいので、このスクリプトは参考程度にして欲しい。
import numpy as np
import matplotlib.pyplot as plt
# Define system parameters
T = 3  # Sampling period
j = 3  # Time delay steps
N = 70  # Number of time steps
# Define system polynomials
A = np.array([1, -1.080, 0.1426, -7.855e-5])
B = np.array([0.9925, 0.8683, 0.01413])
F = np.array([1, 1.080, 1.024])
G = np.array([0.9519, -0.1459, 8.043e-5])
# Initialize variables
y = np.zeros(N)  # System output
y_hat = np.zeros(N)  # Predicted output
u = np.zeros(N)  # Control input
w = np.ones(N)  # Reference signal (step input)
# Simulation loop
for k in range(j, N - j):
    # Compute control input
    B_F = np.convolve(B, F)[:len(B)]
    G_y = np.sum(G[:min(k+1, len(G))] * y[max(0, k-len(G)+1):k+1])
    if np.sum(B_F) != 0:
        u_k = (w[k + j] - G_y) / np.sum(B_F)
    else:
        u_k = 0  # Avoid division by zero
    u_k = np.clip(u_k, -5, 5)  # Input constraints
    u[k] = u_k
    # Compute system output
    y_k = (np.sum(B[:min(k+1, len(B))] * u[max(0, k-len(B)+1):k+1]) -
           np.sum(A[1:min(k+1, len(A))] * y[max(0, k-len(A)+2):k+1]))
    y[k] = y_k
    # Compute predicted output
    y_hat[k] = G_y + np.sum(B[:min(k+1, len(B))] * u[max(0, k-len(B)+1):k+1]) * np.sum(F)
# Plot results
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(range(N), y, 'b', label='y_k (Actual output)')
plt.plot(range(N), y_hat, 'r--', label='y_hat_k (Predicted output)')
plt.xlabel('Time Step')
plt.ylabel('Output')
plt.legend()
plt.title('System Output and Prediction')
plt.grid(True)
plt.subplot(2, 1, 2)
plt.plot(range(N), u, 'r', label='u_k (Control input)')
plt.xlabel('Time Step')
plt.ylabel('Control Input')
plt.legend()
plt.title('Control Input')
plt.grid(True)
plt.tight_layout()
plt.show()