13. 一般化最小分散制御
最小分散制御を適用するには、制御対象は最小位相系で、むだ時間が正確にわかっている必要がある。この条件を緩和するために一般化最小分散制御が提案された。式(1)の線形離散時間モデルの制御対象を考える。$$A(q^{-1})y_k = q^{-j_m} B(q^{-1})u_k + C(q^{-1})e_k \;\;\; \cdots (1)$$ここで、$$A(q^{-1}) = 1 + a_1 q^{-1} + a_2 q^{-2} + \cdots a_n q^{-n} \\ B(q^{-1}) = b_0 + b_1 q^{-1} + \cdots + b_m q^{-m} \\ C(q^{-1}) = 1 + c_1 q^{-1} + c_2 q^{-2} + \cdots + c_l q^{-l}$$である。\(j_m\)は、想定されるむだ時間の最小値で、むだ時間が既知の場合は、\(j_m = j\)、まったく把握できない場合は、\(j_m =1\)とする。
評価関数は、$$J_2 = E\left[ \phi_{k+ j_m} ^2\right] \;\;\; \cdots (2)$$とする。\(\phi_{k + j_m}\)は、一般化出力で、$$\phi_{k + j_m} = P(q^{-1}) y_{k + j_m} + S(q^{-1}) u_k - R(q^{-1})w_{k+j_m}$$である。ここで、$$P(q^{-1}) = 1 + p_1 q^{-1} + p_2 q^{-2} + \cdots p_{n_p} q^{-n_p} \\ S(q^{-1}) = s_0 + s_1 q^{-1} + \cdots + s_{n_s} q^{-n_s} \\ R(q^{-1}) = r_0 + r_1 q^{-1} + r_2 q^{-2} + \cdots + r_{n_r} q^{-n_r}$$である。
13-1. 評価関数\(J_2\)を最小にする制御則
$$P(q^{-1}) C(q^{-1}) = A(q^{-1}) F(q^{-1}) + q^{-j_m} G(q^{-1}) \;\;\; \cdots (3)$$とする。ここで、$$F(q^{-1}) = 1 + f_1 q^{-1} + f_2 q^{-2} + \cdots + f_{j_m -1}q^{-(j_m-1)} \\ G(q^{-1}) = g_0 + g_1 q^{-1} + g_2 q^{-2} + \cdots + g_{n_2} q^{-n_2} , \quad n_2 = \text{max} \left\{n-1, n_p +1-j_m \right\}$$である。
式(1)の両辺に\(q^{j_m} F(q^{-1})\)を掛ける。$$A(q^{-1})F(q^{-1})y_{k+j_m} = B(q^{-1})F(q^{-1})u_k + C(q^{-1})F(q^{-1})e_{k+j_m}$$ 式(3)を使うと、$$P(q^{-1}) C(q^{-1}) y_{k + j_m} = G(q^{-1}) y_k + B(q^{-1}) F(q^{-1}) u_k + C(q^{-1}) F(q^{-1}) e_{k + j_m}$$となる。これより、$$P(q^{-1})y_{k+j_m} =\frac{1}{C(q^{-1})}\left\{G(q^{-1}) y_k + B(q^{-1}) F(q^{-1}) u_k\right\} + F(q^{-1}) e_{k + j_m}$$となる。これを一般化出力の式に代入すると、$$\phi_{k + j_m} = \frac{1}{C(q^{-1})}\left[G(q^{-1}) y_k + \left\{B(q^{-1}) F(q^{-1})+C(q^{-1})S(q^{-1})\right\}u_k \\ - C(q^{-1})R(q^{-1})w_{k+j_m}\right] + F(q^{-1}) e_{k + j_m} \;\;\; \cdots (4)$$である。これを式(2)の評価関数に代入し、\(e_k\)が白色雑音で\(E[e_k]=0\)であることを考慮すると、操作量\(u_k\)は、$$u_k = \frac{C(q^{-1}) R(q^{-1})w_{k+j_m} - G(q^{-1})y_k}{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})} \;\;\; \cdots(5)$$となる。
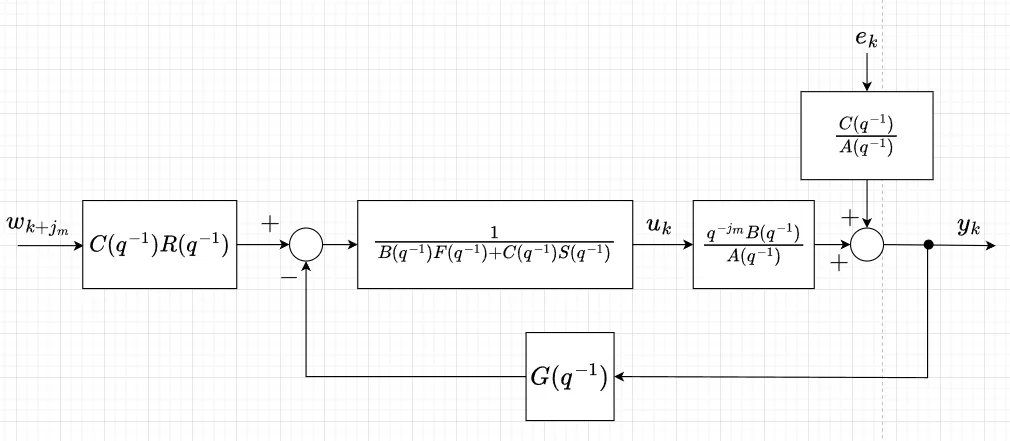
図1に一般化最小分散制御系のブロック線図を示す。
13-2. 水位制御モデルの一般化最小分散制御
12. 最小分散制御(2)で示した数位制御モデルに一般化最小分散制御を適用することを考える。
式(6)で示すむだ時間を有する水位制御モデルをサンプリング周期\(T=3 \text{[s]}\)で離散化する。$$G(s) = \frac{30}{25.04 s^3 + 78.84 s^2 + 41.1 s +1}e^{-9s} \;\;\; \cdots (6)$$
離散化結果は、以下となる。$$A(q^{-1})y_k = q^{-3}B(q^{-1})u_k \\ A(q^{-1})=1−1.080q^{-1}+0.1426q^{-2}−7.855×10^{-5} q^{-3} \\ B(q^{-1})=0.9925+0.8683q^{-1}+0.01413q^{-2}$$式(3)において\(P(q^{-1})=1\)と選ぶと、最小分散制御と同じになるので、$$F(q^{-1}) = 1 + 1.080q^{-1} +1.024q^{-2} \\G(q^{-1}) = 0.9519 - 0.1459q^{-1} + 8.043 \times 10^{-5} q^{-2}$$となる。
ここで、式(4)の一般化出力の重み多項式を\(P(q^{-1})=1, \; S(q^{-1}) = 20, \; R(q{-1}) = 1\)とすると、制御器の極は、式(5)の分母より、\(B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})=0\)を解いて、\(0.1014514\pm j 0.3725104,\quad -0.2787368, \quad -0.0165895\)となり、安定であることが分かる。
図1より、開ループの多項式\(L(q^{-1})\)は、$$L(q^{-1}) = \frac{1}{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})} \frac{q^{-j_m} B(q^{-1})}{A(q^{-1})} F(q^{-1})$$となる。閉ループ制御系の特性多項式\(T(q^{-1})\)は、\(1+L(q^{-1})=0\)なので、式(3)を使ってこの式を整理すると、$$T(q^{-1}) = B(q^{-1})P(q^{-1})+ A(q^{-1})S(q^{-1}) = 0$$となる。\(T(q^{-1})=0\)を解くと、特性根として、\(0.8214875, \quad 0.1655387,\quad 0.0005503\)を得る。これより、システムが安定であることが分かる。
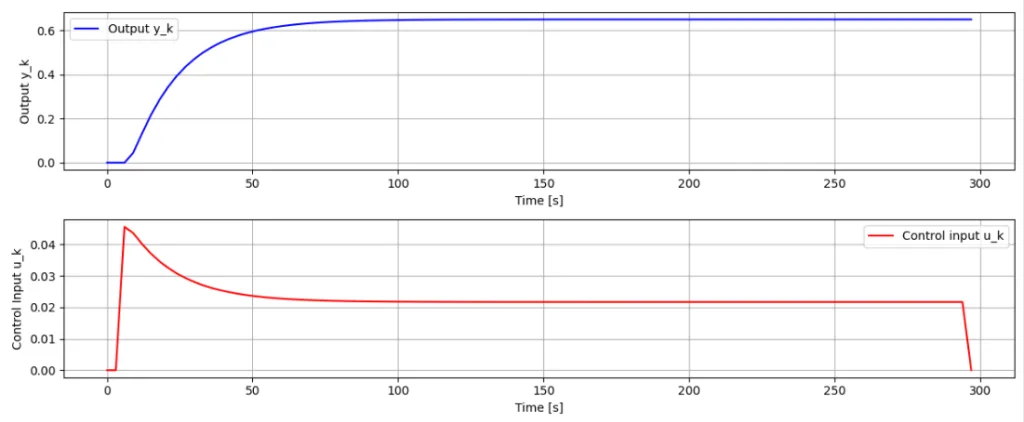
水位制御モデルの一般化分散制御系のPythonスクリプトによるシミュレーションを示す。図2にシミュレーション結果を示す。12. 最小分散制御(2)では、不安定であったシステムが一般化最小分散制御を適用することで安定化できることが分かる。しかし、出力\(y_k\)は60%程度にしか到達しておらず大きな定常位置偏差が生じている。
import numpy as np
import matplotlib.pyplot as plt
# Sampling time
T = 3 # seconds
N = 100 # Number of time steps
# System coefficients
A = [1, -1.080, 0.1426, -7.855e-5]
B = [0.9925, 0.8683, 0.01413]
F = [1, 1.080, 1.024]
G = [0.9519, -0.1459, 8.043e-5]
C = [1] # Assuming C(q^{-1}) = 1
S = 20
R = 1
# Input and output initialization
y = np.zeros(N) # Output
u = np.zeros(N) # Control input
w = np.ones(N) # Step reference input
# Simulation loop
for k in range(2, N - 1):
# Compute u_k
numerator = C[0] * R * w[k] - (G[0] * y[k] + G[1] * y[k - 1] + G[2] * y[k - 2])
denominator = (B[0] * F[0] + B[1] * F[1] + B[2] * F[2]) + (C[0] * S)
u_k = numerator / denominator
# Store control input
u[k] = u_k
# Compute y_k using system equation
y[k + 1] = -A[1] * y[k] - A[2] * y[k - 1] - A[3] * y[k - 2] + B[0] * u_k + B[1] * u[k - 1] + B[2] * u[k - 2]
# Time axis
time = np.arange(0, N * T, T)
# Plot results
plt.figure(figsize=(12, 5))
plt.subplot(2, 1, 1)
plt.plot(time, y, label='Output y_k', color='b')
plt.xlabel('Time [s]')
plt.ylabel('Output y_k')
plt.legend()
plt.grid()
plt.subplot(2, 1, 2)
plt.plot(time, u, label='Control input u_k', color='r')
plt.xlabel('Time [s]')
plt.ylabel('Control Input u_k')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
13-3. 重み調整法による定常偏差の低減
時刻\(k\)における制御偏差\(err_k\)を目標値\(w_k\)と出力\(y_k\)との差\(err_k = w_k - y_k\)で定義する。ここで、出力\(y_k\)は図1より、$$y_k = \frac{B(q^{-1})R(q^{-1})}{T(q^{-1})}w_k + \frac{B(q^{-1})F(q^{-1})+C(q^{-1})S(q^{-1})}{T(q^{-1})}e_k$$と表せる。ここで、$$T(q^{-1}) = B(q^{-1})P(q^{-1})+ A(q^{-1})S(q^{-1})$$である。\(e_k\)は白色雑音なので、制御偏差\(err_k\)の期待値をとると$$E[errr_k] = w_k - \frac{B(q^{-1})R(q^{-1})}{T(q^{-1})}w_k = \frac{T(q^{-1}) - B(q^{-1})R(q^{-1})}{T(q^{-1})} w_k$$となる。目標値\(w_k\)が単位ステップとしたとき、定常偏差の期待値は、最終値定理を使って、$$E[err_\infty] = \lim_{k \to \infty} E[err_k] = \lim_{q \to 1} (1 - q^{-1})\frac{T(q^{-1}) - B(q^{-1})R(q^{-1})}{T(q^{-1})} \cdot \frac{q}{q-1} \\ = \frac{T(1) - B(1)R(1)}{T(1)}$$となる。
13-2.の水位制御モデルで計算すると、$$B(1)=1.875,\quad P(1)=1,\quad A(1)=0.06252, \quad S(1)=20$$となり、\(T(1) = 3.1254\)となる。よって、$$E[err_\infty] = \frac{T(1) - B(1)R(1)}{T(1)} = 0.4001$$ である。これは定常位置偏差が約40%となることを示している。この\(E[err_\infty]\)を0にするには、\(T(1)-B(1)R(1)=0\)すなわち、$$B(1)P(1) + A(1)S(1) - B(1)R(1)=0$$が成立するように重み多項式を設定すればよい。例えば、$$P(q^{-1}) = 1,\quad S(q^{-1}) = \lambda ,\quad R(q^{-1}) = 1 + \lambda\frac{A(1)}{B(1)}$$とすれば良い。
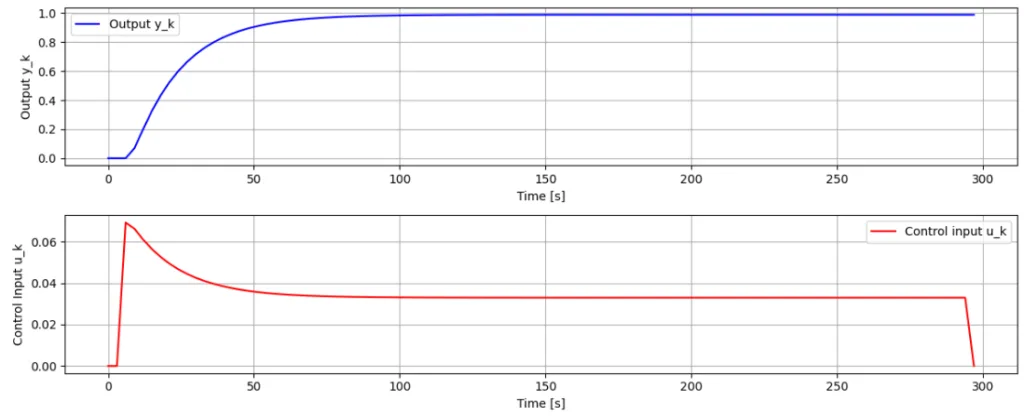
13-2.のPythonスクリプトで、\(R=1.52\)とした場合の時間応答を図3に示す。定常位置偏差が0になっていることが分かる。