2. 線形系のスライディングモード制御

ここでは、式(1)の状態方程式で示す線形時不変のシステムを制御対象とする。$$\dot{x} = Ax + Bu \;\;\; \cdots (1)$$ここで、\(x \in R^n , \quad u \in R^m\)である。また、\(B\)行列の\(m\)個の列ベクトルは、\(b_i \quad (i=1,2, \cdots, m)\)とする。

可変構造系の基本用語の定義

１．可変構造制御系の構造は、ベクトル関数の切換関数\(\sigma(x)\)の符号に支配される。切換関数は\(m\)次元で線形である。$$\sigma(x) = Sx,\quad \sigma(x) = [\sigma_1(x), \sigma_2(x), \cdots ,\sigma_m(x)]^T \;\;\; \cdots (1)$$ $$S = [S_1^T, S_2^T, \cdots , S_m^T]^T$$として、$$\sigma_i(x) = S_i^Tx$$各スカラの切換関数\(\sigma_i(x)\)は、線形な面\(\sigma_i(x)=0\)を含んでおり、切換面と定義される。
２．\(\sigma\)上に任意の初期値\(x_0\)があるならば、全ての\(t \gt t_0\)に対して\(x(t)\)は\(\sigma\)上に常に存在する。このとき、\(x(t)\)はスライディングモード状態にあるという。
３．もし\(\sigma\)上のすべての点が終点であるならば、すなわち、\(\sigma\)上の全ての点に対して\(\sigma\)の両側からの軌道が\(\sigma\)に向かう状態のとき、切換面\(\sigma\)は滑り面と呼ばれる。
４．状態が滑り面の方向に向かうときや滑り面にたどり着く条件は到達条件と呼ばれる。
以上の定義より、\(m\)個の入力を持つ\(n\)次系のシステムは、\(2^m-1\)個の切換面を持つ。また、すべての切換面\(\sigma_i \quad (i=1,2,\cdots , m)\)の交線は\(n-m\)次元の一つの切換面\(\sigma_e\)になる。\(\sigma_e\)は、すべての切換面が最終的に到達しなければならない最終切換面と呼ばれる。$$\sigma_e = \left\{x | \sigma(x) = Sx = 0\right\}= \sigma_1 \cap \sigma_2 \cap \cdots \cap \sigma_m$$ \(\sigma_e\)に関するスライディングモードは最終スライディングモードと呼ばれる。

到達条件と到達モード

状態が滑り面の方に向かって動き、かつ、滑り面に到達する条件を到達条件と呼ぶ。到達条件下でのシステムの軌跡は到達モード、または到達位相と呼ばれる。到達条件を指定するためのアプローチとして、以下のような方法がある。

１）直接切換関数法：この方法は初期に提案されたもので、スライディング面（切換関数）を状態変数の線形結合などによってあらかじめ定義し、その面に状態を到達させるように制御入力を設計する手法で、理論的には明快かつ強力な方法であるが、実際の制御系への適用には困難が伴う。特に、多入力のスライディングモードに対して適用するのは困難とされている。
切換関数の設計では、 明確化された制御目標を達成するために、適切な形状を持つ切換関数\(\sigma(x)\)を設計する。ここで、\(x\)はシステムの状態ベクトルで、この切換関数は、スライディングモードが発生するべき面\(\sigma(x)=0\)を定義する。
制御入力の設計では、設計された切換関数に基づいて、システムの状態がスライディング面に到達し、その面上を滑るように、不連続な制御入力\(u\)を設計する。一般的な制御入力の形は、$$u = \begin{cases} u^+ & \sigma(x) > 0 \\ u^- & \sigma(x) < 0 \end{cases} $$ここで、\(u^+\)と\(u^-\)は、\(\sigma(x)\)の符号に応じて選択される制御入力で、これらの値は、システムのダイナミクスと制御目標を考慮して適切に決定される。次に、設計された切換関数と制御入力が、システムの状態を有限時間内にスライディング面に到達させるための条件（到達条件）を満たすか確認する。一般的な到達条件としては、以下の Lyapunov 関数\(V=\frac{1}{2}\sigma^2(x)\)の時間微分\(\dot V = \sigma(x) \dot{\sigma}(x)\)が負になるように制御入力を設計する。

２）リアプノフ関数法：リアプノフ関数法を用いることで、システムの状態が有限時間内にスライディング面に到達することを保証するための制御入力の設計指針を得ることができる。リアプノフ関数法では、系の安定性を解析するために、正定値関数\(V(x)\)（リアプノフ候補関数）を導入し、その時間微分\(\dot V (x)\)が負定または半負定であることを示すことで、平衡点の安定性を保証する。最も一般的な形は、以下の正定値関数で、$$V(x)=\frac{1}{2}\sigma^2(x)$$システムの状態がスライディング面に近づき、最終的に到達するためには、\(V(x)\)が時間とともに減少し、最終的にゼロになる必要がある。従って、このリアプノフ候補関数の時間微分\(\dot V (x)\)が負になるように制御入力 \(u\)を設計することが、到達条件を満たすための基本的な考え方となる。$$\dot V (x) = \sigma(x) \dot{\sigma}(x)$$ここで、\(\dot{\sigma}(x)\)はスライディング変数\(\sigma(x)\)の時間微分であり、システムのダイナミクスと制御入力\(u\)に依存する。到達条件を保証するためには、\(\dot V(x) \lt 0\)（または、\(\dot V(x) \leq -\eta |\sigma(x)| \text{ここで、} \eta \gt 0 \) ）となるように制御入力\(u\)を設計する。これは、\(\sigma(x)\)と\(\dot{\sigma}(x)\)が常に逆符号を持つように制御入力を選択することを意味する。具体的には、以下のような条件を満たすように制御入力\(u\)を設計する。
・\(\sigma(x) \gt 0\)のとき、\(\dot{\sigma}(x) \lt 0\)
・\(\sigma(x) \lt 0\)のとき、\(\dot{\sigma}(x) \gt 0\)
これにより、\(\sigma(x) \dot{\sigma}(x) \lt 0\)となり、\(\dot{V}(x) \lt 0\)が保証され、\(\sigma(x)\)は時間とともに0に近づき、最終的にスライディング面に到達する。
より具体的な到達条件としては、指数的到達条件が用いられる。状態 x(t)x(t)x(t) がスライディング面 σ(x)=0\sigma(x) = 0σ(x)=0 に指数的に到達するためには、状態がスライディング面に向かって収束する速度が指数関数的である必要があります。これを数式で表現すると、$$\dot{\sigma}(x) = -\alpha |\sigma(x)| \quad (\alpha > 0)$$ここで、\(\alpha\)は正の定数で、指数的に減衰する速度を決定する。この式は、スライディング面に到達する速度が指数的に速くなることを保証する。指数的到達を保証するために、リアプノフ関数を使ってその安定性を確認する方法が一般的です。リアプノフ関数として、スライディング面に向かって収束するエネルギー関数を定義する。$$V(x) = \frac{1}{2} \sigma(x)^2$$このリアプノフ関数の時間微分\(\dot{V}(x)\)を計算する。$$\dot{V}(x) = \sigma(x) \dot{\sigma}(x)$$上記の指数的到達条件$$\dot{\sigma}(x) = -\alpha |\sigma(x)|$$を代入すると、次のようになる。$$\dot{V}(x) = -\alpha |\sigma(x)|^2$$ \(\dot{V}(x)\)が負であるため、リアプノフ関数は単調減少となる。これにより、状態\(x(t)\)がスライディング面に指数的に収束することが保証される。
リアプノフ関数の時間微分が負であることから、状態 \(\sigma(x)\)がスライディング面に向かって指数的に収束することが確認できる。具体的には、次のように収束する。$$|\sigma(t)| \leq |\sigma(t_0)| e^{-\alpha (t - t_0)}$$これにより、状態 \(\sigma(x)\)は時間\(t\)が経過するにつれて、指数的に0に近づいていくことがわかる。

線形システムへの適用例

線形時不変システムへのスライディングモードの適用として、状態方程式が$$\dot x = Ax + Bu $$で表される以下の2次元システムを扱う。ここで、状態ベクトル：\(x \in R^2\)、入力：\(u \in R^1\)、行列： $$A = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}, \quad B = \begin{bmatrix} 0 \\ 1 \end{bmatrix}$$スライディングモード制御によって目標状態 $$x_{ref} = [1, 0]^T \text{（= 単位ステップ）}$$へ状態を追従させるようにする。
スライディング面の定義は、 $$S = C(x - x_{ref})$$として、目標値への誤差に基づいた制御にする。

※線形システムにスライディングモード制御を適用した場合の数値シミュレーション用Pythonスクリプト例を以下に示す。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# System matrices
A = np.array([[0, 1],
              [0, 0]])
B = np.array([[0],
              [1]])
# Sliding surface vector: S = C(x - x_ref)
C = np.array([1, 2])
# Control gain
k = 5.0
# Reference state (unit step)
x_ref = np.array([1.0, 0.0])
# Sliding Mode Control input with reference tracking
def control_input(x):
    S = C @ (x - x_ref)
    return -k * np.sign(S)
# System dynamics under SMC
def dynamics(t, x):
    u = control_input(x)
    dxdt = A @ x + B.flatten() * u
    return dxdt
# Initial condition
x0 = [0.0, 0.0]  # Start from origin
# Time span and time points
t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 500)
# Numerical simulation
sol = solve_ivp(dynamics, t_span, x0, t_eval=t_eval)
# Compute control input u
u_values = np.array([control_input(x) for x in sol.y.T])
# Plot 1: State vs Time
plt.figure(figsize=(10, 4))
plt.plot(sol.t, sol.y[0], label='$x_1(t)$')
plt.plot(sol.t, sol.y[1], label='$x_2(t)$')
plt.axhline(y=1.0, color='red', linestyle='--', linewidth=1.0, label='Reference $x_1$')
plt.title('State Trajectories Over Time (with Step Reference)')
plt.xlabel('Time [s]')
plt.ylabel('States')
plt.grid(True)
plt.legend()
plt.tight_layout()
# Plot 2: Control Input vs Time
plt.figure(figsize=(10, 4))
plt.plot(sol.t, u_values, label='$u(t)$', color='orange')
plt.axhline(0, color='gray', linestyle='--', linewidth=0.8)
plt.title('Control Input Over Time')
plt.xlabel('Time [s]')
plt.ylabel('Control Input $u(t)$')
plt.grid(True)
plt.legend()
plt.tight_layout()
# Plot 3: Phase Plane (x1 vs x2)
plt.figure(figsize=(5, 5))
plt.plot(sol.y[0], sol.y[1], color='darkblue', label='Trajectory')
plt.scatter(x0[0], x0[1], color='red', label='Initial State')
plt.scatter(x_ref[0], x_ref[1], color='green', label='Reference State')
plt.axhline(0, color='gray', linestyle='--', linewidth=0.8)
plt.axvline(0, color='gray', linestyle='--', linewidth=0.8)
plt.title('Phase Plane Plot')
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.grid(True)
plt.legend()
plt.axis('equal')
plt.tight_layout()
plt.show()

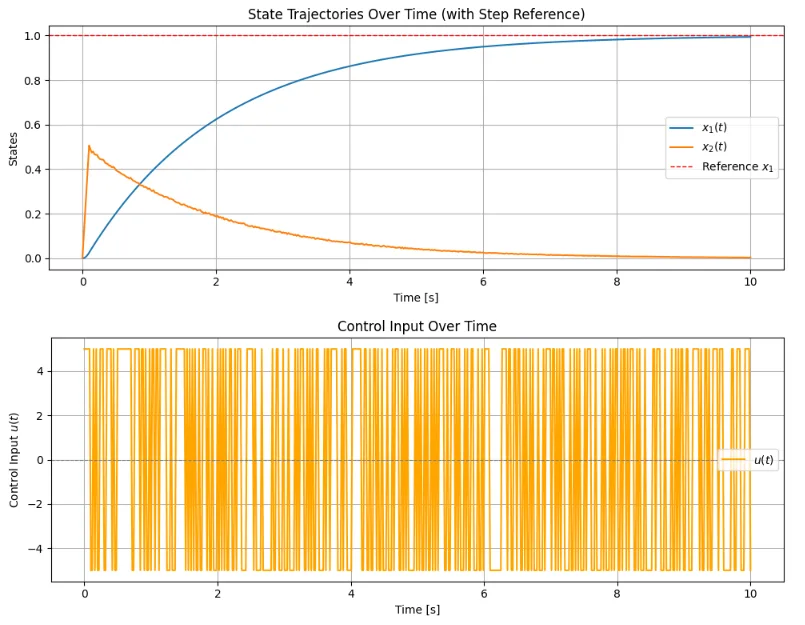
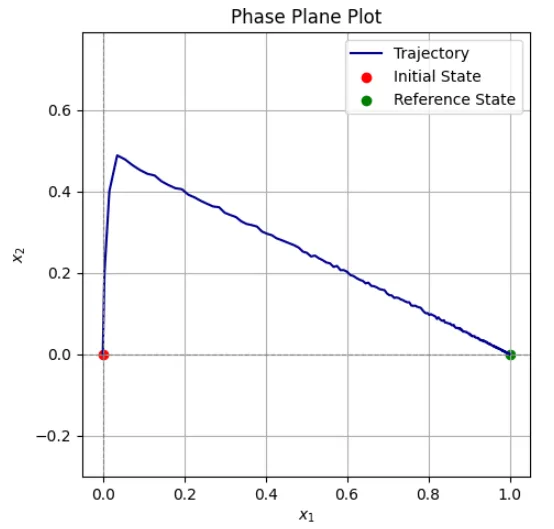
図１に状態量の時間応答（ステップ応答）を示す。状態量\(x_1(t)\)は、目標値（単位ステップ）に追従していることが分かる。当然、状態量\(x_2(t)\)は0に収束する。また、入力\(u(t)\)は、図に示すように、連続的な切換動作を繰り返すことになる。これは、スライディングモード制御の実装の難しさ（高速な切換やチャタリングなどの問題）を表している。図２は、\(x_1(t),\; x_2(t)\)による位相平面上の軌跡である。図のように初期値（原点）から切換線に向かって移動し、\(x_2(t)=0.5\)の点でスライディングモードに移行した後に目標値の\(x_{ref} = [1, 0]^T\)に到達している。スライディングモードの過程では、\(x_2(t)\)に小さな揺らぎが見られる。これは、入力\(u(t)\)の頻繁な切換による。\(x_1(t)\)は、\(x_1(t) = \int x_2(t)\)なので、この揺らぎはシステムの安定な動作に実質的に影響しない。