3. スライディングモード切換方式

スライディングモード制御則の設計では、スライディングモードに入る方式の選択と制御則の構造を予め指定するかどうかの問題がある。ここでは、スライディングモードに入る方式を考える。
制御対象は、線形時不変システムで以下とする。
$$\dot{x} = Ax + Bu,\quad x \in R^n, \; u \in R^m \\ \text{切換関数}\sigma(x) = Sx, \quad \sigma(x) = [\sigma_1(x), \sigma_2(x), \cdots, \sigma_m(x)]^T \\ S=[S_1^T, S_2^T, \cdots, S_m^T]^T \\ \sigma_i(x) = S_i^Tx$$

固定次数切換方式

この方式は、スライディング面への到達速度を一定の次数で制御することを目指す。制御入力が状態に応じて決定され、スライディング面への到達に一定の速度や次数を与えることができる。ここで、スライディング面 \(\sigma (x)\)を\(\sigma(x) = Sx\)と定義する。これは、状態ベクトル\(x(t)\)の関数で、システムが到達すべき平面（もしくは超平面）を示している。\(S\)は設計パラメータで、スライディング面の方向を決定する。固定次数切換方式では、スライディング面への到達が固定次数で行われるように制御入力\(u(t)\)を設計する。
スライディング面への到達速度（次数）の制御を具体的に示すために、次のような高次切換関数を導入する。$$ \dot{\sigma}(x) = -\alpha |\sigma(x)|^n \quad (\alpha > 0, n > 0)$$ここで、\(n\)は固定次数を意味し、制御入力は状態 \(\sigma(x)\)がスライディング面に到達する速度を決定する。この式では、状態がスライディング面に到達する際の収束速度が次数\(n\)によって制御され、指数的な収束が保証される。スライディング面への到達を固定次数で行うために、制御入力を次のように設計する。$$u(t) = -K \cdot \text{sign}(\sigma(x)) - \lambda \cdot \dot{\sigma}(x)$$ここで、\(K\)は制御ゲイン、\(\lambda\)は設計パラメータで、\(\text{sign}(\sigma(x))\)はスライディング面に向かって状態を収束させるための符号関数である。\(\lambda \cdot \dot{\sigma}(x)\)によってスライディング面に向かって状態が収束する速度を調整する。
微分方程式 \(\dot{\sigma}(x) = - \alpha |\sigma(x)|^n \)の一般解を考える。
１）\(\sigma(x) \gt 0\)のとき
このとき、\(∣\sigma(x)∣=\sigma(x)\)なので、微分方程式は$$\frac{d \sigma}{dt}= -\alpha \sigma^n$$となる。これを変数分離して積分する。$$\sigma^{-n} d\sigma = - \alpha dt$$両辺を積分する。以下、\(\sigma(x(t)) \equiv \sigma(t)\)と記述する。
・\(n=1\)の場合： $$ \int \frac{1}{\sigma} d\sigma = \int -\alpha dt , \quad \ln|\sigma| = -\alpha t + C_1 \\ |\sigma| = e^{-\alpha t + C_1} = e^{C_1} e^{-\alpha t} $$ \(\sigma \gt 0\)より、 $$ \sigma(t) = A e^{-\alpha t} \quad (A = e^{C_1} \gt 0) $$
・\(n \neq 1\)の場合: $$ \int \sigma^{-n} d\sigma = \int -\alpha dt , \quad \frac{\sigma^{-n+1}}{-n+1} = -\alpha t + C_1 \\ \sigma^{1-n} = (1-n)(-\alpha t + C_1) $$ $$ \sigma(t) = [(1-n)(C_1 - \alpha t)]^{\frac{1}{1-n}} $$ 初期条件 \(\sigma(t_0) = \sigma_0 \gt 0\)を用いると、 $$ \sigma_0^{1-n} = (1-n)(C_1 - \alpha t_0) \Rightarrow C_1 = \frac{\sigma_0^{1-n}}{1-n} + \alpha t_0 $$ 従って、 $$ \sigma(t) = \left[ \sigma_0^{1-n} + (1-n)\alpha (t_0 - t) \right]^{\frac{1}{1-n}} $$
２）\(\sigma(x) \lt 0\)のとき
このとき、\(|\sigma(x)|=−\sigma(x)\)なので、微分方程式は$$ \frac{d \sigma}{dt} = - \alpha(-\sigma)^n = - \alpha (-1)^n \sigma^n$$となる。
・\(n\)が偶数（ \(n=2m, m \in Z^+ \) ）の場合：$$ \frac{d\sigma}{dt} = -\alpha \sigma^{2m} $$ これは１）と同様の形になり、解は$$ \sigma(t) = - \left[(1-2m)(C_1 - \alpha t) \right]^{\frac{1}{1-2m}}, \quad​ （\sigma \lt 0 \text{の初期条件を考慮})$$となる。
・\(n\)が奇数 (\(n=2m+1, m \in Z \geq 0\)​)の場合: $$ \frac{d\sigma}{dt} = -\alpha (-\sigma)^{2m+1} = \alpha \sigma^{2m+1} $$ $$ \sigma^{-(2m+1)} d\sigma = \alpha dt $$ $$ \frac{\sigma^{-2m}}{-2m} = \alpha t + C_1 $$ $$ \sigma^{-2m} = -2m(\alpha t + C_1) $$ $$ \sigma(t) = [-2m(\alpha t + C_1)]^{-\frac{1}{2m}} $$ 初期条件 \(\sigma(t_0) = \sigma_0 \lt 0\)を用いると、 $$ \sigma_0^{-2m} = -2m(\alpha t_0 + C_1) \Rightarrow C_1 = -\frac{\sigma_0^{-2m}}{2m} - \alpha t_0 $$ したがって、 $$ \sigma(t) = \left[ \frac{\sigma_0^{-2m}}{2m} - \alpha (t - t_0) \right]^{-\frac{1}{2m}} $$
３）\(\sigma(x)=0\)のとき
\(\dot{\sigma} (x)=0\)なので、\(\sigma(t)=0\)は自明な解である。
＊有限時間収束について
特に\(0 \lt n \lt 1\)の場合、\(\sigma(t)\)は有限時間で 0 に到達する。例えば、\(\sigma_0 \gt 0\)のとき、\(\sigma(t)=0\)となる時間\(t_f\)は、$$0 = \left[\sigma_0^{1-n} - (n-1)\alpha(t_f - t_0)\right]^{\frac{1}{1-n}} \\ \sigma_0^{1-n} = (n-1)\alpha(t_f - t_0) \\ t_f = t_0 +\frac{\sigma_0^{1-n}}{(n-1)\alpha}$$となる。\(n \lt 1\)なので、\(1-n \gt 0\)であり、\(t_f\)は有限の値を持つことがわかる。

固定次数切換方式を線形2次系に適用した例

線形2次系の制御対象に対して固定次数切換方式のスライディングモード制御を適用した場合のシミュレーションを行う。線形2次系の状態方程式は次のように書ける$$\dot{x}(t) = A x(t) + B u(t)$$ここで、状態ベクトル\(x(t) \in R^2\)は、システムの状態（例えば位置と速度）を表し、制御入力 \(u(t)\) は操作量である。行列\(A\)はシステムのダイナミクスを決定し、\(B\)は制御入力\(u(t)\)のシステムへの影響を示す。
具体的には、状態方程式を以下のように定義する。$$\dot{x}_1(t) = x_2(t) \\ \dot{x}_2(t) = -a_1 x_1(t) - a_2 x_2(t) + b_1 u(t)$$ここで、\(x_1(t)\)は位置、\(x_2(t)\)は速度、\(a_1\)と\(a_2\)はシステムパラメータ、\(b_1\)は制御入力が速度に及ぼす影響を示す。目標値を単位ステップとし、状態\(x(t) = [x_1(t), x_2(t)]\)に対して、\(x_1(t) \to 1.0,　\quad x_2(t) \to 0\)（= 静止した状態で目標位置に達する。）とする。スライディング面 \(\sigma(x)\)を$$\sigma(x) = (x_1 - x_{\text{target}}) + x_2$$と定義する（\(​x_{\text{target}} \)は、単位ステップ）。制御入力\(u(t)\)はスライディングモード制御則に基づいて、$$u(t) = -K \cdot \text{sign}(\sigma(x)) - \lambda \cdot \dot{\sigma}(x)$$ と設計する。
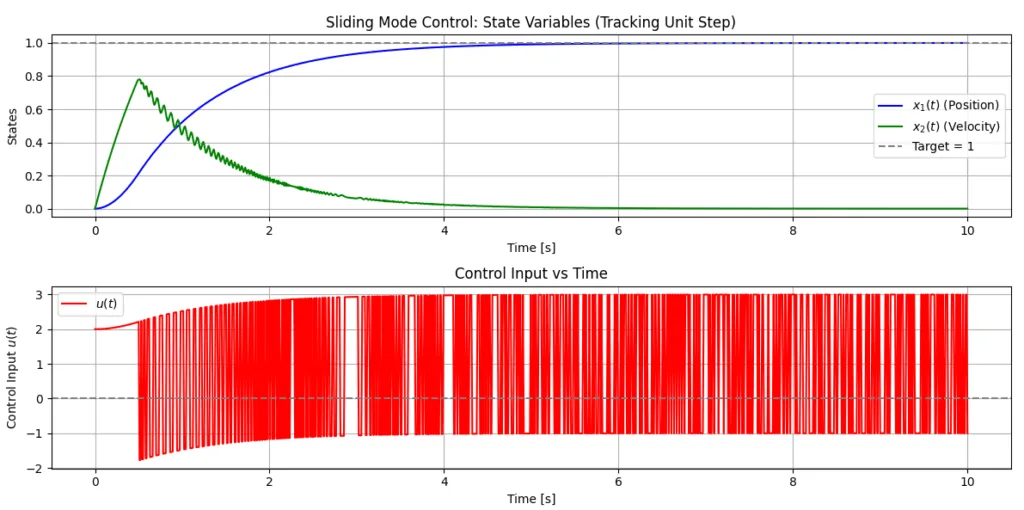
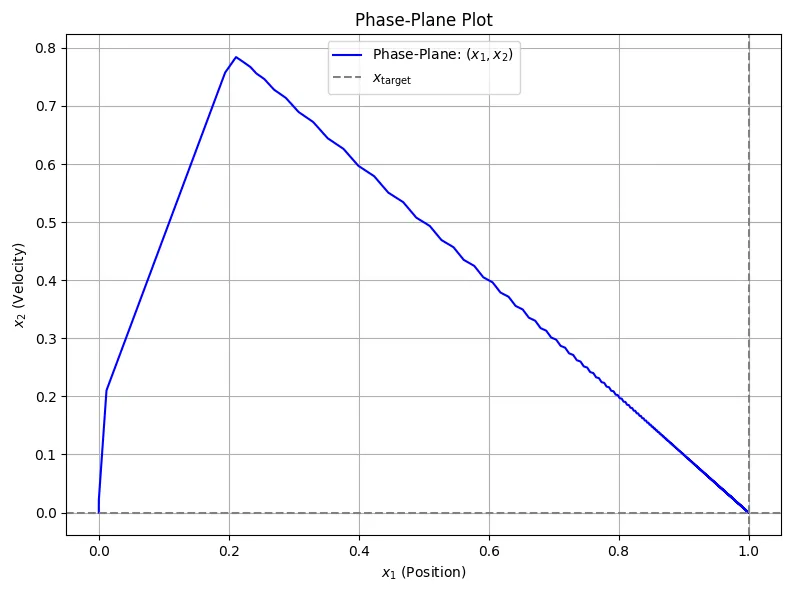
※Pythonスクリプトの例とシミュレーション結果を図１、図２に示す。図２より、\(x_1=0.2,\quad x_2=0.8\)近傍でスライディング面に到達し、スライディングモードで目標値に到達する様子が分かる。また、図１の制御入力\(u(t)\)の時間応答を見ると、スライディング面に到達するまで加速して速度を増加させ、スライディング面に到達した後、スライディングモードで減速しながら目標値に近づいていることが分かる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# System parameters
a1 = 1.0
a2 = 1.0
b1 = 1.0
K = 2.0
lambda_ = 1.0
# Initial and target values
x_target = 1.0          # Target position (unit step)
x_0 = np.array([0.0, 0.0])  # Initial position and velocity
t0 = 0
t_end = 10
# System dynamics with target tracking
def system_dynamics(t, x):
    # Define sliding surface
    sigma = (x[0] - x_target) + x[1]
    # Estimate sigma_dot without control input first
    dx1 = x[1]
    dx2_wo_u = -a1 * x[0] - a2 * x[1]
    sigma_dot_est = x[1] + dx2_wo_u
    # Control input (sliding mode control)
    u = -K * np.sign(sigma) - lambda_ * sigma_dot_est
    # System dynamics with control input
    dx2 = dx2_wo_u + b1 * u
    return [dx1, dx2]
# Solve the system
sol = solve_ivp(system_dynamics, [t0, t_end], x_0, dense_output=True)
# Extract results
x1_vals = sol.y[0]
x2_vals = sol.y[1]
# Time points for evaluation
t_vals = np.linspace(t0, t_end, 1000)
x_vals = sol.sol(t_vals)
# Post-calculate control input and sliding surface
sigma_vals = (x_vals[0, :] - x_target) + x_vals[1, :]
dx2_wo_u_vals = -a1 * x_vals[0, :] - a2 * x_vals[1, :]
sigma_dot_vals = x_vals[1, :] + dx2_wo_u_vals
u_vals = -K * np.sign(sigma_vals) - lambda_ * sigma_dot_vals
# Plot state trajectories
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(t_vals, x_vals[0, :], label=r'$x_1(t)$ (Position)', color='b')
plt.plot(t_vals, x_vals[1, :], label=r'$x_2(t)$ (Velocity)', color='g')
plt.axhline(x_target, color='gray', linestyle='--', label='Target = 1')
plt.xlabel('Time [s]')
plt.ylabel('States')
plt.title('Sliding Mode Control: State Variables (Tracking Unit Step)')
plt.grid(True)
plt.legend()
# Plot control input
plt.subplot(2, 1, 2)
plt.plot(t_vals, u_vals, label=r'$u(t)$', color='r')
plt.axhline(0, color='gray', linestyle='--')
plt.xlabel('Time [s]')
plt.ylabel('Control Input $u(t)$')
plt.title('Control Input vs Time')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
# Phase-plane plot (x1 vs x2)
plt.figure(figsize=(8, 6))
plt.plot(x1_vals, x2_vals, label=r'Phase-Plane: $(x_1, x_2)$', color='b')
plt.xlabel(r'$x_1$ (Position)')
plt.ylabel(r'$x_2$ (Velocity)')
plt.title('Phase-Plane Plot')
plt.axhline(0, color='gray', linestyle='--')
plt.axvline(x_target, color='gray', linestyle='--', label=r'$x_{\text{target}}$')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

最終スライディングモード切換方式

最終スライディングモード切換方式（Terminal Sliding Mode Control, TSMC）は、線形スライディングモード制御（Linear Sliding Mode Control, LSMC）が漸近的な安定性しか保証しないのに対し、有限時間内でのスライディング面への到達と平衡点への収束を可能にする非線形制御手法である。LSMCでは、通常、線形なスライディング関数\(\sigma(x)=Sx\) が用いられ、スライディングモード上でのダイナミクスは線形となる。これにより、状態は漸近的に平衡点に収束するが、有限時間内での収束は保証されない。これに対し、TSMCでは、非線形なスライディング関数を導入することで、スライディングモード上での状態が有限時間内に平衡点に到達する特性を持たせる。一般的な最終スライディング関数の一例は、$$\sigma(x) = x + \beta|x|^\gamma \text{sign}(x), \quad (0 \lt \gamma \lt 1,\quad \beta \gt 0)$$である。さらに、多次元システムの場合、状態ベクトル\(x=[x_1​,x_2​,...,x_n​]^T\) に対して、$$\sigma_i(x) = x_i +\beta_i|x_i| \gamma_i \text{sign}(x_i), \quad (0 \lt \gamma_i \lt 1, \quad \beta_i \gt 0, \; i=1,2,\ldots,n)$$ここで、\(0 \lt \gamma \lt 1\)であることが、有限時間収束を実現するための鍵となります。この非線形項 \(|x|\gamma \text{sgn}(x)\)の導入により、平衡点近傍での収束速度が速くなり、有限時間収束が保証される。
TSMCの設計は、主に以下の2つのステップで行われる。
・最終スライディング関数の設計: 所望の有限時間収束特性（収束時間など）を考慮して、適切な非線形スライディング関数\(\sigma(x)\)を設計する。パラメータ\(\beta\)と\(\gamma\)の選択が重要となる。
・制御入力の設計: 設計されたスライディング関数\(\sigma(x)\)を用いて、到達条件（スライディング面への有限時間到達を保証する条件）を満たすような制御入力\(u(t)\)を設計する。一般的な制御入力は、不連続な切換項を含み、スライディング変数の符号に基づいて制御方向を切り替える形となる。$$u(t)=−K \text{sign}(\sigma(x))−f(x,t)$$ここで、\(K\)は制御ゲイン、\(f(x,t)\)はシステムの理想的なダイナミクスを補正するための項などである。

最終スライディングモード切換方式を線形2次系に適用した例

線形2次系の制御対象に対して最終スライディングモード切換方式のスライディングモード制御を適用した場合のシミュレーションを行う。状態方程式を以下のように定義する。$$\dot{x}_1(t) = x_2(t) \\ \dot{x}_2(t) = -a_1 x_1(t) - a_2 x_2(t) + b_1 u(t)$$ここで、\(x_1(t)\)は位置、\(x_2(t)\)は速度、\(a_1\)と\(a_2\)はシステムパラメータ、\(b_1\)は制御入力が速度に及ぼす影響を示す。目標値を単位ステップとし、状態\(x(t) = [x_1(t), x_2(t)]\)に対して、\(x_1(t) \to 1.0,　\quad x_2(t) \to 0\)（= 静止した状態で目標位置（\(x_{target}\)に達する。）とする。スライディング面 \(\sigma(x)\)は、$$\sigma(x)=(x_1​−x_{target}​)+\beta|x_1​−x_{target}|^\gamma​\cdot⋅\text{sign}(x_1​−x_{target}​) + x_2​$$と定義する。また、制御入力\(u(t)\)はスライディングモード制御則に基づいて、$$u(t) = −K\cdot \text{sign}(\sigma(x))−f(x,t)$$と設計する。ここで、\(f(x,t) = -a_1 x_1 - a_2 x_2\)で、システムの理想的なダイナミクスを補正するための項である。
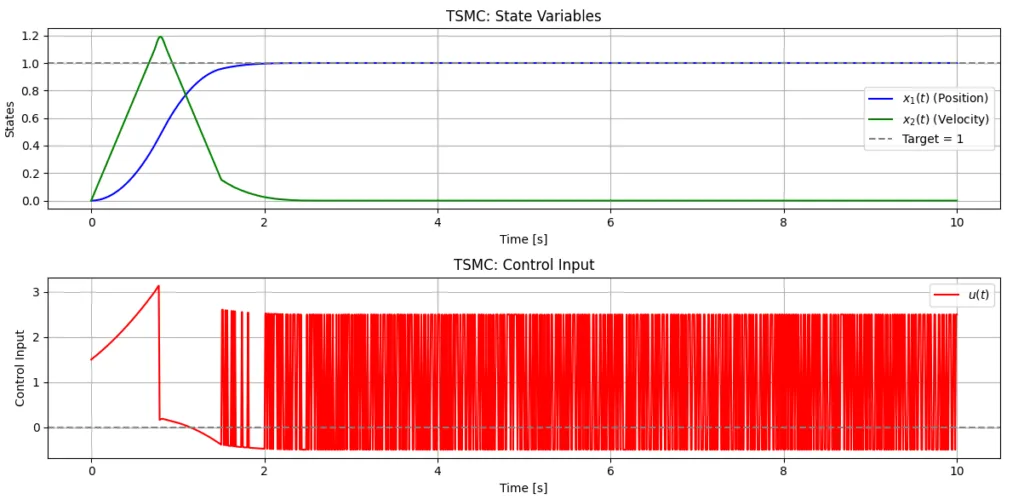
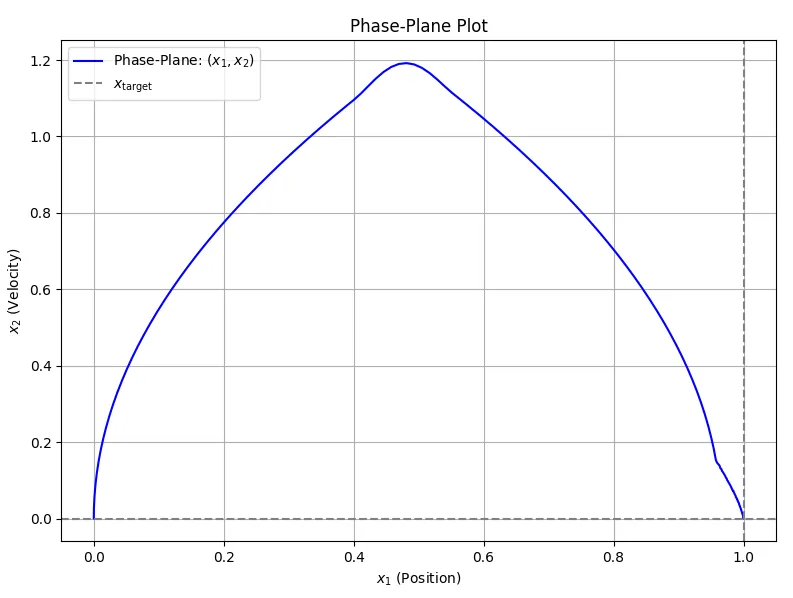
※Pythonスクリプトの例を示す。また、シミュレーション結果を図３、図４に示す。図３の制御入力\(u(t)\)を見ると、この方式では、加速・減速により目標値の近傍まで達した後、スライディング面に到達してスライディングモードに入り、目標値に達する。図４より、\(x_1=0.95,\quad x_2=0.15\)近傍でスライディング面に到達し、スライディングモードに入ることが分かる。このように、この方式では目標値近傍に早く到達するため、図１に比べて目標値に到達する時間が短縮できる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# System parameters
a1 = 1.0     # coefficient for x1
a2 = 1.0     # coefficient for x2
b1 = 1.0     # control gain
K = 1.5      # sliding mode control gain
# Terminal sliding mode parameters
beta = 1.0
gamma = 0.7  # must satisfy 0 < gamma < 1
# Target value (unit step)
x_target = 1.0
# Initial state: x1 = 0 (position), x2 = 0 (velocity)
x0 = [0.0, 0.0]
# Time domain
t0, t_end = 0, 10
t_eval = np.linspace(t0, t_end, 1000)
# Terminal sliding surface
def sigma(x):
    e = x[0] - x_target
    return e + beta * np.abs(e)**gamma * np.sign(e) + x[1]
# Equivalent dynamics compensation term
def f_xt(x):
    return -a1 * x[0] - a2 * x[1]
# Control law
def control_input(x):
    return -K * np.sign(sigma(x)) - f_xt(x)
# System dynamics under control
def system_dynamics(t, x):
    u = control_input(x)
    dx1 = x[1]
    dx2 = -a1 * x[0] - a2 * x[1] + b1 * u
    return [dx1, dx2]
# Solve the system
sol = solve_ivp(system_dynamics, [t0, t_end], x0, t_eval=t_eval)
# Extract results
x1_vals = sol.y[0]
x2_vals = sol.y[1]
t_vals = sol.t
sigma_vals = np.array([sigma(x) for x in sol.y.T])
u_vals = np.array([control_input(x) for x in sol.y.T])
# Plot state variables
plt.figure(figsize=(12, 6))
# Plot x(t) (position and velocity)
plt.subplot(2, 1, 1)
plt.plot(t_vals, x1_vals, label=r'$x_1(t)$ (Position)', color='b')
plt.plot(t_vals, x2_vals, label=r'$x_2(t)$ (Velocity)', color='g')
plt.axhline(x_target, color='gray', linestyle='--', label='Target = 1')
plt.xlabel('Time [s]')
plt.ylabel('States')
plt.title('TSMC: State Variables')
plt.grid(True)
plt.legend()
# Plot control input u(t)
plt.subplot(2, 1, 2)
plt.plot(t_vals, u_vals, label=r'$u(t)$', color='r')
plt.axhline(0, color='gray', linestyle='--')
plt.xlabel('Time [s]')
plt.ylabel('Control Input')
plt.title('TSMC: Control Input')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
# Phase-plane plot (x1 vs x2)
plt.figure(figsize=(8, 6))
plt.plot(x1_vals, x2_vals, label=r'Phase-Plane: $(x_1, x_2)$', color='b')
plt.xlabel(r'$x_1$ (Position)')
plt.ylabel(r'$x_2$ (Velocity)')
plt.title('Phase-Plane Plot')
plt.axhline(0, color='gray', linestyle='--')
plt.axvline(x_target, color='gray', linestyle='--', label=r'$x_{\text{target}}$')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()