26. 積分型最適レギュレータ
目標値がステップ関数であるサーボシステムの構成として、積分型最適レギュレータがある。これは、入力\(u(t)\) はできるだけ緩やかに変化させながら制御対象の出力\(y(t)\) と一定目標値\(r(t)\) との偏差\(e(t)\) をできるだけ速やかに零に収束させようとするものである。
連続時間系に対する積分型最適レギュレータ
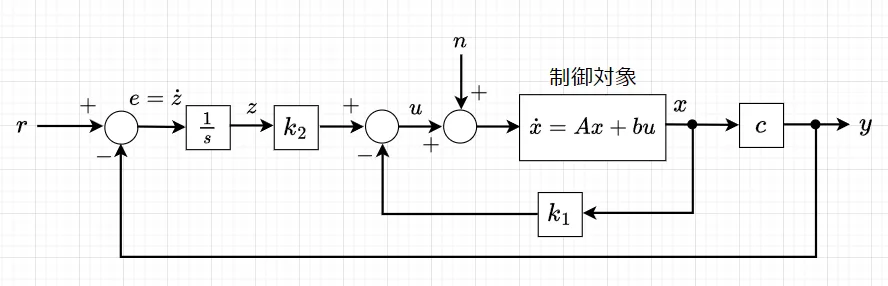
図1に連続時間系に対する積分型最適レギュレータのブロック線図を示す。制御対象には状態フィードバックが施されており、その前段に積分器が置かれ、積分器の入力は、制御対象の出力\(y\)と目標値\(r\)との偏差\(e\)である。この構成の開ループシステムは、原点に極を持つ(\(1/s\)があるから)。従って、状態フィードバックの係数ベクトル\(k_1\)と積分器の係数\(k_2\)が閉ループシステムが安定になるように選ばれていれば、内部モデル原理により、ステップ状の外乱\(n\)に対する制御対象の出力\(y\)は目標値\(r\)のステップ関数に追従し、定常偏差は零となる。状態フィードバック係数ベクトル\(k_1\)と積分器の係数\(k_2\)は最適レギュレータの手法により決定される。
制御対象の状態方程式、出力方程式を$$\dot{x} = A x + bu \;\;\; \cdots (1)\\ y = c x $$とする。ただし、\(x(t) \in R^{n \times 1} , \;\; u(t) \in R , \;\; y(t) \in R\)である。また、制御対象の伝達関数\(P(s) = c(sI -A)^{-1} b\)の零点が\(s=0\)に存在しないものとする。つまり、\(P(0) = -cA^{-1} b \neq 0\)とする。制御対象の状態方程式を基に、図1を参考に考える。状態\(x(t)\)の微分\(\dot{x}(t)\)と偏差\(e(t)\)を新たな状態変数ベクトルとする。$$e(t) = r(t) - y(t) = r(t) - cx \;\;\; \cdots (2)$$であり、式(1)、式(2)を微分すると、$$\frac{d}{dt} \begin{bmatrix} \dot{x} \\ e \end{bmatrix} = \begin{bmatrix} A & 0 \\ -c & 0\end{bmatrix} \begin{bmatrix} \dot{x} \\ e\end{bmatrix} + \begin{bmatrix} b \\ 0\end{bmatrix} \dot{u} \;\;\; \cdots (3) \\ e = \begin{bmatrix} 0 & 1 \end{bmatrix} \begin{bmatrix} \dot{x} \\ e\end{bmatrix} $$の\(n+1\)次元の拡大システムが求まる。式(3)について評価関数$$J = \int_0^{+\infty} \left\{ \begin{bmatrix} \dot{x} \\ e \end{bmatrix} ^T Q \begin{bmatrix} \dot{x} \\ e \end{bmatrix} + r |\dot{u}|^2 \right\} dt \;\;\; \cdots (4)$$を最小とする\(u(t)\)を求める。ただし、\(Q\)は\(n+1\)次の正定対称行列、\(r\)は正の実数である。式(4)の評価関数\(J\)を小さくすることは、入力\(u(t)\)の変化\(\dot{u}(t)\)を小さく抑えて、拡大システムの状態変数ベクトル\([\dot{x}(t) \;\;\;\; e(t)]^T\)を速やかに零にする最適レギュレータ問題となっている。従って、式(4)の評価関数\(J\)を最小にする最適な入力\(\dot{u}(t)\)は、状態変数ベクトル\([\dot{x}(t) \;\;\;\; e(t)]^T\)の状態フードバックで与えられる。これは、もとの制御対象の状態方程式(式(1))で考えると、制御対象への入力\(u(t)\)と状態変数\(x(t)\)の変化をできるだけ小さく抑えながら、出力\(y(t)\)と偏差\(e(t)\)を速やかに零に収束させる制御システムを設計することになる。
制御対象が可制御、可観測であれば、拡大システムも可制御、可観測である。従って、その最適レギュレータ問題の解は、状態フィードバック$$\dot{u} = -r^{-1}\begin{bmatrix} b \\ 0 \end{bmatrix}^T P \begin{bmatrix} \dot{x} \\ e \end{bmatrix}$$で与えられる。\(P \in R^{(n+1) \times (n+1)}\)は、拡大システムの係数行列から作られるリッカチ行列方程式$$ \begin{bmatrix} A & 0 \\ -c & 0 \end{bmatrix}^T P + P \begin{bmatrix} A & 0 \\ -c & 0 \end{bmatrix} - r^{-1} P \begin{bmatrix} b \\ 0 \end{bmatrix} \begin{bmatrix} b \\ 0 \end{bmatrix}^T P = -Q \;\;\; \cdots (5)$$の解で、\((n+1)\)次の正定対称行列である。
ここで、$$\begin{bmatrix} k_1 & k_2 \end{bmatrix} = r^{-1}\begin{bmatrix} b \\ 0 \end{bmatrix}^T P , \;\;\;\;\; k_1 \in R^{1 \times n} , \;\;\; k_2 \in R$$とおくと、$$\dot{u} = -k_1 \dot{x} - k_2 e$$と書けるので、これを積分すると、$$u = - k_1 x -k_2 \int_0^t e(\tau) d\tau$$を得る。つまり、図1に示すように、操作入力\(u(t)\)は、制御対象の\(x(t)\)による状態フィードバックと偏差\(e(t)\)の積分値のフィードバックとして与えられることが分かる。
偏差\(e(t)\)の積分を$$z(t) = \int_0^t e(\tau) d\tau$$とおくと、積分型最適レギュレータの状態方程式は、$$\frac{d}{dt} \begin{bmatrix} x \\ z \end{bmatrix} = \left\{ \begin{bmatrix} A & 0 \\ -c & 0 \end{bmatrix} - \begin{bmatrix} b \\ 0 \end{bmatrix} \begin{bmatrix} k_1 & k_2 \end{bmatrix} \right\} \begin{bmatrix} x \\ z \end{bmatrix} + \begin{bmatrix} 0 \\1 \end{bmatrix} r + \begin{bmatrix} b \\0 \end{bmatrix} n \\ y = \begin{bmatrix} c & 0 \end{bmatrix} \begin{bmatrix} x \\ z \end{bmatrix} $$と表せる。
積分型最適レギュレータの例
連続時間制御対象を$$\dot{x}(t) = \begin{bmatrix} 2 & 1 \\ 0 & 1 \end{bmatrix} x +\begin{bmatrix} 1 \\ 2 \end{bmatrix} u , \;\;\; x(0) = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \\ y = \begin{bmatrix} 1 & 2 \end{bmatrix} x$$とする。2次形式評価関数の重みを$$Q = \begin{bmatrix} 1 & & \\ & 1 & \\ & & 1\end{bmatrix}, \;\;\; r=1$$として、積分型最適レギュレータを設計する。拡大システムの状態方程式は、$$\frac{d}{dt} \begin{bmatrix} \dot{x} \\ e \end{bmatrix} = \begin{bmatrix} 2 & 1 & 0 \\ 0 & 1 & 0 \\ -1 & -2 & 0 \end{bmatrix} \begin{bmatrix} \dot{x} \\ e \end{bmatrix} + \begin{bmatrix} 1 \\ 2 \\ 0 \end{bmatrix} u , \;\;\;\; e = \begin{bmatrix} 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \dot{x} \\ e \end{bmatrix}$$となる。式(5)のリッカチ行列方程式を解くと、$$P = \begin{bmatrix} 30.702132 & -10.084218 & 6.4248839 \\ -10.084218 & 4.5822586 & -2.7124419 \\ 6.4248839 & -2.7124419 & 2.3160713\end{bmatrix}$$が求まる。よって、$$u = -k_1 x - k_2 \int_0^t e(\tau) d\tau$$ $$k_1 = \begin{bmatrix} 10.533696 & -0.9197006 \end{bmatrix} , \;\;\; k_2 =1$$となる。また、閉ループ系の極は、$$-2.242604 \pm 0.8719052j \;\;\;\;\; -1.2090873$$である。
※リッカチ行列方程式の解\(P\)やフィードバックゲインベクトル\(k_1,\;k_2\)、閉ループ系の極などは、以下のScilabスクリプトにより求めた。
Scilabスクリプト
//26. 積分型最適レギュレータ
clear;clf();
i=%i;
//制御対象の状態方程式
A0=[2 1; 0 1];
b0=[1; 2];
c0=[1 2];
x0 = [0;0]; /* 初期状態変数 / sysP=syslin('c',A0,b0,c0);
//制御対象の固有値
spec(A0);
//可制御性のチェック
Uc=cont_mat(A0,b0); n=rank(Uc);
//拡大システムの定義
A= [2 1 0; 0 1 0; -1 -2 0]; b= [1 ; 2 ; 0];
//重み係数
Q=[1 0 0 ; 0 1 0 ; 0 0 1]; r=1;
//状態フィードバック係数の決定 P=riccati(A,binv(r)b',Q,'c','eigen');
f=inv(r)b'P;
//極配置の確認
cpoles=spec(A-bf);
//積分型最適レギュレータのステップ応答
t=0:0.01:10;
//閉ループ系の状態方程式
A2=A-b*f;
b2=[0; 0; 1] ;
c2 = [1 2 0]
sysP2=syslin('c',A2,b2,c2);
y=csim('step',t,sysP2);
scf(0);plot(t',y');
//閉ループ系の極(固有値)
spec(A2);
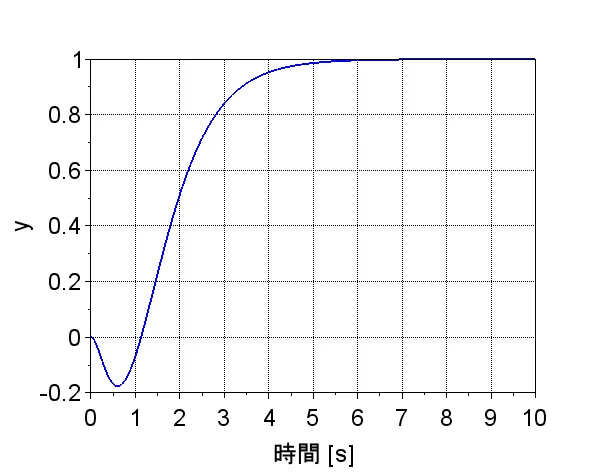
図2に積分型最適レギュレータを適用したシステムのステップ応答の例を示す。図から定常偏差が零に出来ていることが分かる。

