1. 機械学習のタイプ
機械学習には、データの種類や目的に応じていくつかの主要なタイプがある。それぞれのタイプには特徴的なアルゴリズムと応用範囲がある。機械学習システムは、学習中に受ける人間の関与の程度、タイプによって分類できる。主要なタイプは、教師あり学習、教師なし学習、強化学習、半教師あり学習、自己教師あり学習、の5種類である。
機械学習システムの主要タイプ
教師あり学習(Supervised Learning)
入力データ(特徴量)と、それに対応する正解データ(ラベル)が与えられた状態でモデルを学習させる。
用途:「回帰(数値予測):住宅価格予測」、「分類(カテゴリー分け):スパムメールの分類」
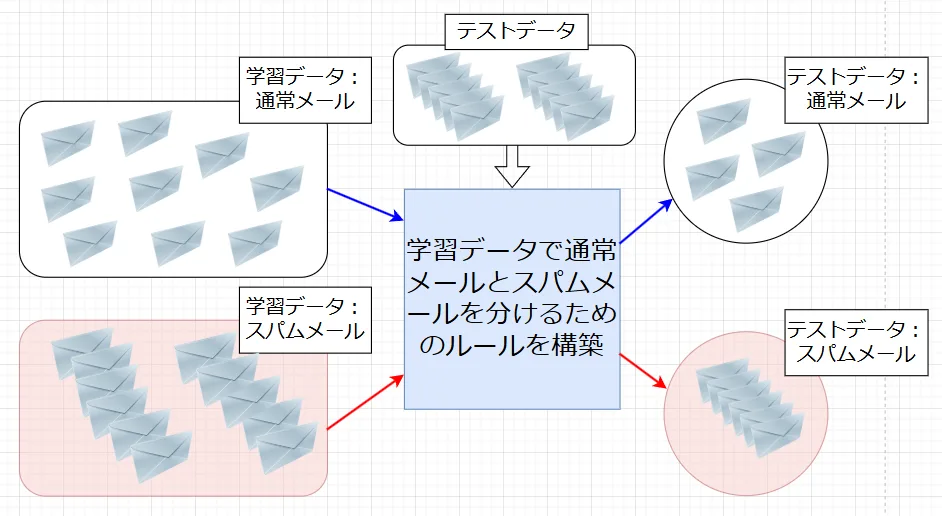
受信した電子メールがスパム(迷惑メール)かどうかを自動判定するには、教師あり学習が有効である。図1に示すように、以下の手順で教師あり学習を実施する。
1.過去に受信したメールにたいして、人間側が「通常のメール」と「スパムメール」の正解(ラベル)を付与した学習データを読み込ませる。
2.学習データでコンピュータがルールを作る。
3.ルールに従って「通常のメール」と「スパムメール」の正解を付与したテストデータをちゃんと分けることができれば良い。
具体的なアルゴリズムとしては、「線形回帰」、「サポートベクターマシーン(SVM)」、「ランダムフォレスト」、「決定木」、「k近傍法(kNN)」などがある。
(ラベル付き学習セット)
教師なし学習(Unsupervised Learning)
正解ラベルのないデータを使い、データの構造やパターンを発見する。
用途:「クラスタリング(グループ分け):顧客セグメント分析」、「次元削減:データの可視化や効率化」
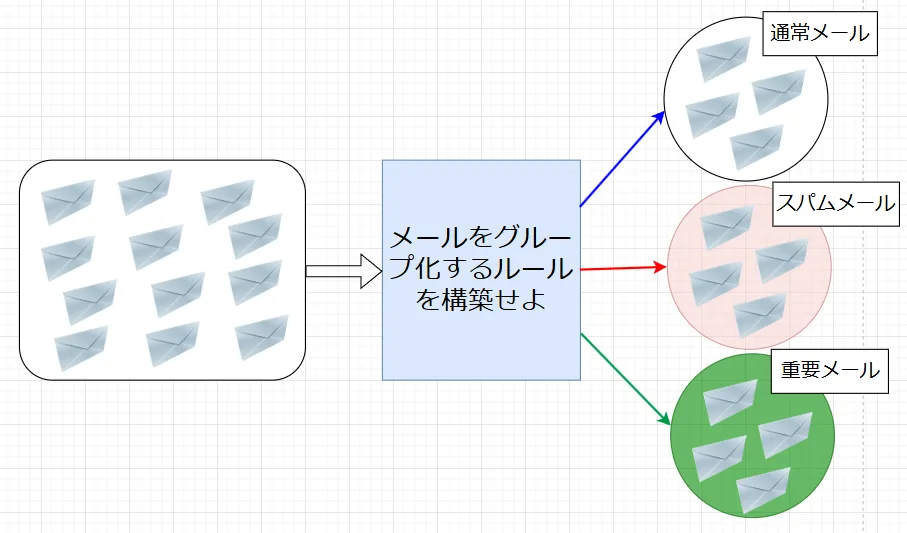
教師あり学習の場合、受信したメールを「スパム」「通常」と正解ラベルを人間側が付与する。これに対し、「どれがスパムか通常か分からない状況で、とにかくメールの特徴からグループ分けしたい」という場合には、教師なし学習を実施する。図2参照。
具体的なアルゴリズムとしては、「クラスタリング」、「主成分分析」、「k平均法(k-means)」などがある。
(ラベルのない学習セット)
強化学習(Reinforcement Learning)
エージェント(学習主体)が環境との相互作用を通じて、報酬を最大化するような行動を学習する。
用途:「ゲームAI(囲碁、将棋)」、「自律走行車の制御」
強化学習は、試行錯誤を繰り返すことで、ある目標を達成するための最適な行動を学習する 機械学習の手法で、エージェントが環境と相互作用しながら、報酬を最大化するような行動を学習していく。
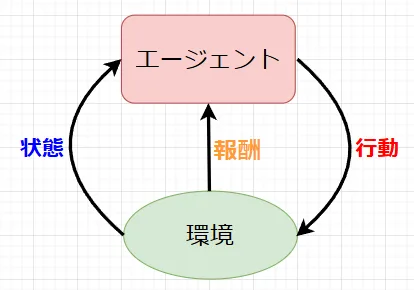
図3に示すように、エージェントが、環境に対して行動を起こし、その結果として得られる報酬や状態の変化を基に学習する。正しい答えが与えられるのではなく、行動の結果として得られる報酬や罰によって学習を進める。また、即座の報酬だけでなく、将来的な報酬も考慮しながら、最適な行動を選択する。
*強化学習の構成要素
・エージェント: 学習を行う主体
・環境:エージェントが行動する場所
・状態:環境の状態を表す情報
・行動:エージェントが実行できる動作
・報酬:行動の結果として得られる評価
半教師あり学習(Semi-Supervised Learning)
教師ありと教師なしの中間で、一部のラベル付きデータと大量のラベルなしデータを用いる。半教師あり学習では、ラベル付けされたデータとラベル付けされていないデータの両方を使って学習する。教師あり学習では全てのデータにラベルが必要であるが、半教師あり学習では、一部のデータにのみラベルが付いていれば学習することができる。
半教師あり学習により、以下が期待できる。
・データのラベル付けのコスト削減: 全てのデータをラベル付けするのは、時間とコストがかかる作業である。半教師あり学習では、一部のデータにのみラベル付けすることで、コストを削減できる。
・大量のデータの活用:ラベル付けされていないデータを有効活用することで、モデルの精度向上を期待できる。
・教師あり学習の限界克服:教師あり学習では、十分な量のラベル付きデータが必要だが、半教師あり学習では、少ないラベル付きデータでも学習が可能である。
アルゴリズムの例としては、以下がある。
・ラベル伝播法(Label Propagation):ラベル付きデータのラベルを、データの類似性やクラスタの構造をもとにラベルなしデータに伝播していく方法。
・自己学習(Self-Training):初期モデルをラベル付きデータで学習し、そのモデルを使ってラベルなしデータに疑似ラベルを付けて再学習する方法。
・生成モデル(Generative Models):ラベル付きデータとラベルなしデータを組み合わせてデータの分布をモデリングし、ラベルの予測を行う。
・コントラスト学習(Contrastive Learning):ラベルなしデータの中で類似したデータ同士を近づけ、異なるデータを遠ざけるように学習する。
自己教師あり学習(Self-Supervised Learning)
データ自体から疑似ラベルを生成して学習する新しいアプローチで、画像や自然言語処理の分野で注目されている。自己教師あり学習では、データ自体を利用して疑似ラベルを生成し、そのラベルを用いてモデルを学習する。この方法では、従来のように人間がラベルを付ける必要がなく、未ラベルデータを効率的に活用できる。自己教師あり学習は、特に画像認識や自然言語処理(NLP)の分野で注目されており、ディープラーニングモデルの事前学習において多用されている。
自己教師あり学習は、次のようなステップで進行する。
・タスク設計:元データを部分的に加工し、自己教師ありタスク(疑似ラベルを予測するタスク)を設定する。
・モデルの学習:加工されたデータを使い、モデルが疑似ラベルを予測することで学習する。
・事前学習モデルの活用:学習済みモデルを別のタスクに転用することで、高精度な予測を実現。
バッチ学習とオンライン学習
機械学習における学習方法には、大きく分けてバッチ学習とオンライン学習の2種類がある。それぞれの学習方法には特徴やメリット・デメリットがあり、どのようなシステムで、どのようなデータに対してどのような学習を行うかによって最適な手法は異なる。
バッチ学習
バッチ学習は、全ての学習データを一度にまとめて読み込み、一度の学習でモデルのパラメータを更新する方法。ただし、新しいデータが追加されるたびに、最初から再学習する必要がある。
バッチ学習の特徴:
・全データを用いて学習するため、学習結果が安定しやすい。
・一般的に高精度なモデルが得られる。
バッチ学習のメリット:
・安定した学習:データ全体を考慮して学習するため、パフォーマンスが安定する。
・高精度:大量のデータを一括で使用することで、複雑なパターンを学習しやすい。
・再現性が高い:学習結果がデータセットに依存するため、同じデータで学習すれば同じ結果が得られる。
バッチ学習のデメリット:
・全データをメモリに読み込む必要があるため、大規模データには不向き。
・大規模データを一括処理するため、メモリや計算負荷が高い。
・データの分布が変化した場合、モデルを再学習する必要がある。
用途としては、「画像認識(大量の固定データで学習するディープラーニングモデル)」、「医療診断(静的な患者データの分析)」などがある。
オンライン学習
オンライン学習は、新しいデータが到着するたびにモデルを逐次的に更新する。つまり、データを1つずつ、または小さなバッチ単位で順次読み込み、その都度モデルのパラメータを更新する方法となる。データは一度に全て揃っているわけではなく、ストリームとして提供されることが前提である。オンライン学習の特徴:
・データが連続的に生成される場合や、データの分布が時間とともに変化する場合に適している。
・モデルをリアルタイムに更新できる。
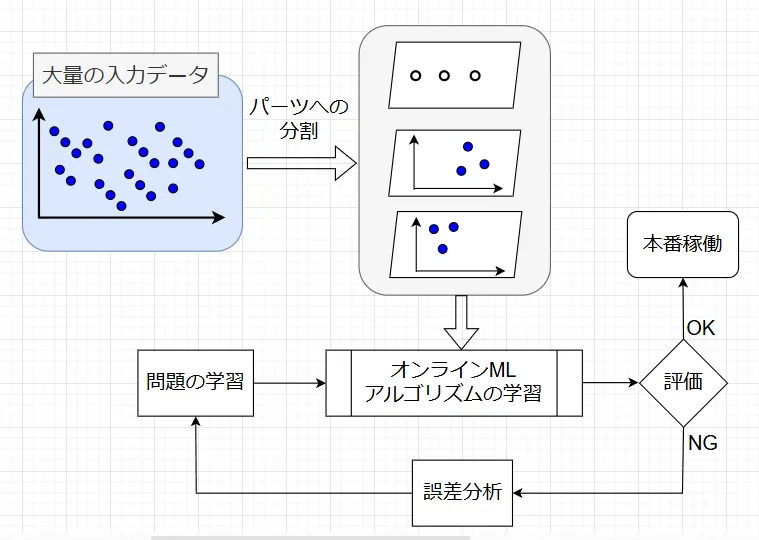
図4に大きなデータセットをオンライン学習で処理する場合の手順を示す。アルゴリズムは、データをパーツに分解することでデータの一部をロードして、それを基に学習を実行し、大量の入力データをすべて処理し終わるまで処理を繰り返す。
オンライン学習のメリット:
・リアルタイム対応:新しいデータを即座に反映できるため、変化する環境に適応可能。
・計算コストが低い:データを小分けにして学習するため、メモリ消費を抑えられる。
・適応性:時間経過とともにモデルが新しいデータに適応する。
オンライン学習のデメリット:
・学習結果が不安定になる場合がある。データが少ない場合やノイズが多い場合、モデルが過剰適応(オーバーフィッティング)する可能性がある。
・バッチ学習に比べて、一般的に精度が低い。
・履歴データの喪失、古いデータが考慮されなくなる場合がある。
用途としては、「フィンテック(株価予測や不正取引検出)」、「レコメンデーションシステム(ユーザ行動に基づくリアルタイム提案)」、「自動運転(センサデータを基にした瞬時の判断)」などがある。
インスタンスベース学習とモデルベース学習
インスタンスベース学習とモデルベース学習は、機械学習アルゴリズムを分類する方法の一つで、学習プロセスや予測の方法が異なる。それぞれの手法には特徴、利点、課題がある。
インスタンスベース学習
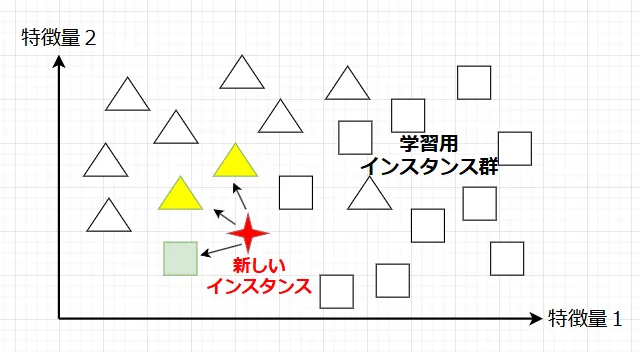
インスタンスベース学習は、過去の事例(インスタンス)をそのまま記憶し、新しいデータに対して、最も近い過去の事例を参照して予測を行う手法です。明示的なモデルを構築せず、トレーニングデータ自体が予測の基盤となる。「記憶ベース学習」とも呼ばれる。
インスタンスベース学習の特徴:
・過去の事例を単純に記憶するため、複雑なモデルを構築しない。
・新しいデータが来ても、過去の事例との類似度を計算するだけで予測が可能。
・学習プロセスは単純で高速。
インスタンスベース学習のアルゴリズム例:
k近傍法(k-Nearest Neighbors, k-NN):新しいデータポイントに対して、保存されたデータから距離が近い\(k\)個を見つけ、多数決や平均で予測を行う。
局所加重回帰(Local Weighted Regression):データの近傍のみを考慮して回帰を行う。
インスタンスベース学習のメリット:
・単純で直感的:データを直接使うため、複雑なモデリングが不要。
・動的な適応:新しいデータをそのまま追加することで、モデルの更新が簡単。
・非線形問題への適用:データ間の複雑な関係も学習可能。
インスタンスベース学習のデメリット:
・計算コスト:過去の事例を全て保持する必要があるため、メモリコストが高い。
・スケーラビリティ:大量のデータがある場合、ストレージや検索時間が問題になる。
・ノイズへの感度:ノイズや外れ値に影響を受けやすい。
用途としては、「小規模データセットの分類や回帰」、「パーソナライズされたシステム(例: レコメンデーション)」などがある。
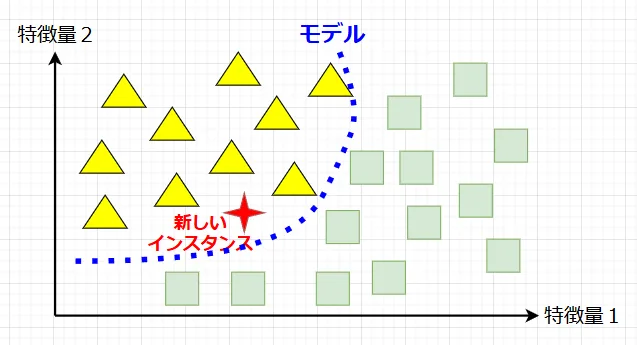
モデルベース学習
モデルベース学習は、過去の事例から一般化されたモデルを構築し、そのモデルを用いて新しいデータに対して予測を行う手法。トレーニングデータを使って明示的なモデルを構築し、そのモデルを用いて予測を行う。モデルは、データのパターンを抽出し、一般化された関数として表現される。
モデルベース学習の特徴:
・学習フェーズでは時間がかかることがあるが、予測は高速。
・データセット全体を必要とせず、学習後はモデルのみを保持する。
モデルベース学習のアルゴリズム例:
・線形回帰(Linear Regression):データ間の関係を直線で表現するモデル。
・サポートベクトルマシン(SVM):ハイパープレーンを用いてデータを分類。
・ニューラルネットワーク:非線形問題にも対応できる柔軟なモデル。
・決定木やランダムフォレスト:データの特徴を階層構造で捉えるモデル。
モデルベース学習のメリット:
・予測が高速:一度モデルを構築すれば、予測時には少ない計算で済む。
・一般化能力:トレーニングデータから抽象的なパターンを学習し、新しいデータにも適用可能。
・データ効率性:モデルだけを保持するため、大規模データにも対応しやすい。
モデルベース学習のデメリット:
・モデル設計の難しさ:適切なアルゴリズムやハイパーパラメータを選ぶ必要がある。
・過学習のリスク:トレーニングデータに過剰に適応し、新しいデータに対応できない場合がある。
・初期学習コスト:モデル構築に時間や計算リソースがかかる。
用途としては、「予測が頻繁に求められるリアルタイムシステム」、「大規模データセットを用いた学習(例: 音声認識、画像認識)」などがある。
ノーフリーランチ定理
ノーフリーランチ定理(No Free Lunch Theorem, NFL)は、すべての最適化問題や機械学習アルゴリズムにおいて、「特定の問題クラスを仮定しない場合、すべてのアルゴリズムの性能は平均的に等しい」という主張を示している。
*定理の前提条件
最適化問題の定式化
関数空間 \(\mathcal{F}\):\(\mathcal{F}\) はすべての可能な関数(問題)の集合。
例えば、入力\(x\)に対して出力\(f(x)\)を与える全関数のセット。
アルゴリズム \(A\):アルゴリズム\(A\)は関数\(f\)の値を一部サンプリングして、最適な解を探索する。
性能評価:各アルゴリズムの性能は、関数 \(f\)に対する結果(例えば、探索効率や解の正確性)で評価される。
*仮定
・すべての問題に対して偏りがない、完全なランダム性を仮定する。
・問題空間(関数空間 \(\mathcal{F}\))の関数\(f\)はすべて等確率で出現する。
*平均性能の計算
アルゴリズム\(A\)の性能を評価するため、関数\(f\)に対する性能値を定義する。
例えば、ある入力集合\(S\) に基づいて、探索点\(x\)が最適解にどれだけ近いかを評価する。$$P_A(f) = \text{アルゴリズム } A \text{ による関数 } f \text{ の性能値}$$ \(\mathcal{F}\) 内のすべての関数\(f\)に対する平均性能は次のように定義される。:$$\langle P_A \rangle = \frac{1}{|\mathcal{F}|} \sum_{f \in \mathcal{F}} P_A(f)$$ここで、\(|\mathcal{F}|\)は関数空間の関数の総数である。
*アルゴリズム間の性能差の比較
同様に、別のアルゴリズム\(B\)に対する平均性能は次のように表される。:$$\langle P_B \rangle = \frac{1}{|\mathcal{F}|} \sum_{f \in \mathcal{F}} P_B(f)$$ここで、すべての関数\(f\)が等確率で選ばれるという仮定のもとでは、\(P_A(f)\)と\(P_B(f)\)の振る舞いが対称的である。この対称性により、次のような関係が成立する。$$\langle P_A \rangle = \langle P_B \rangle$$すなわち、関数空間全体での平均的な性能は、どのアルゴリズムも等しいという結論が得られる。
以上より、次のことが言える。
・アルゴリズム\(A\)が特定の関数\(f_1\)に特化して高性能を示す場合、必然的に他の関数\(f_2\) では性能が悪化する。
・全体で見ると、すべての関数にわたる平均性能は均一化される。
*注意:ただし、実際の問題空間はランダムでないことが多く、現実世界ではノーフリーランチ定理の仮定は完全には適用されない。しかしながら、この定理は、アルゴリズムの選択や設計において、問題の特性を考慮する重要性を強調しているといえる。
線形回帰アルゴリズムと最小二乗法
線形回帰アルゴリズム
概要:
線形回帰アルゴリズムは、入力データ(説明変数)と出力データ(目的変数)の間の関係を直線または超平面で表現する機械学習モデルである。
モデルが「線形」であることを前提に、予測や回帰分析を行う。
特性:
・線形回帰はデータの関係を表現するモデル全体を指す。
・モデルには複数の「学習アルゴリズム」が適用できます(例: 最小二乗法、確率的勾配降下法など)。
・学習アルゴリズムを用いて、モデルのパラメータ(回帰係数)を最適化する。
最小二乗法(最小二乗法の詳細はこちらへ)
概要:最小二乗法は、線形回帰モデルのパラメータ(回帰係数)を計算するための具体的な手法の1つで、モデルの誤差(観測値と予測値の差)を最小化するアルゴリズムである。他の手法(例えば、勾配降下法)と異なり、数学的な直接解を導出する。
線形回帰モデルの学習手段の1つであり、二乗誤差を最小にする回帰係数を算出する。他のアルゴリズムと比べて効率的に計算できる場合があるが、大規模データでは計算負荷が高くなることがある。
まとめ
線形回帰アルゴリズムは、説明変数と目的変数の関係をモデル化し、学習・予測する枠組み全体であり、最小二乗法は、その枠組みの中でモデルを学習するための具体的な数学的手法の1つ。

