16. 特殊関数Ⅱ（微分方程式）

ルジャンドルの微分方程式

ルジャンドルの微分方程式は、球対称性や直交性を持つ関数を特徴付ける重要な微分方程式で、その解であるルジャンドル関数は、数学と物理学の多くの分野で用いられる。
ルジャンドルの微分方程式は、二階の線形常微分方程式で、次の形をしている。$$(1 - z^2) \frac{d^2x}{dz^2} - 2z\frac{dx}{dz} + \nu(\nu + 1) x = 0 \;\;\; \cdots (1)$$ここで、
・\(x=x(z)\) は未知関数
・\(\nu\) は非負整数または一般の実数（通常は整数）
・\(z\) は独立変数（通常 \(-1 \leq z \leq 1\)の範囲で定義）。\(z\)は極座標の方位角\(\theta\)と\(z=\cos \theta\)という関係があるので、 \(-1 \leq z \leq 1\)の範囲で考えることが多い。
式(1)で、\(\frac{1}{2}(1-z)=t\)と変数変換すると、$$t(1-t)x'' +(1-2t)x' +\nu(\nu +1)x=0$$という、\(a=-\nu, b=\nu+1,c=1\)の超幾何微分方程式になる。

ルジャンドル多項式

\(\nu =n\)のとき\(P_n(z)\)は\(n\)次の多項式になる。\(z=1-2t\)とするとき、定義より、$$P_n(z) =\sum_{k=0}^n \frac{(-n)_k (n+1)_k}{(1)_k k!}t^k = \sum_{k=0}^n \frac{(-1)^k (n+k)!}{(n-k)!(k!)^2}t^k$$である。また、ルジャンドルの多項式 \(P_n(z)\) は、次数\(n\)のルジャンドル微分方程式を満たす解で、次の形式で定義できる。$$P_n(z) = \frac{1}{2^n n!} \frac{d^n}{dz^n} (z^2 - 1)^n $$この形式は、一般的なルジャンドルの多項式を生成する直接的な方法である。なお、これはルジャンドル多項式のロドリーグの公式と呼ばれている。
低次のルジャンドル多項式をロドリーグの公式で計算すると以下となる。
\(n=0\)：$$P_0​(z) = \frac{1}{2^0 0!}\frac{d^0}{dz^0}(z^2-1)^0=1$$ \(n=1\)：$$P_1(z) = \frac{1}{2^1 1!}\frac{d}{dz}(z^2-1)^1=\frac{1}{2}2z = z$$ \(n=2\)：$$P_2​(z) = \frac{1}{2^2 2!}\frac{d^2}{dz^2}(z^2-1)^2=\frac{1}{8}\frac{d^2}{dz^2}(z^4 -2z^2 +1) = \frac{1}{8}(12z^2-4) = \frac{1}{2}(3z^2-1)$$

ベッセルの微分方程式

ベッセル関数は、円柱関数とも呼ばれ、波動方程式を円柱座標で考えるとき、動径方向を記述する関数として現れる。三角関数は減衰しない波を記述するが、ベッセル関数は遠くにいくに従って減衰していく波を記述する。
ベッセル関数が従う微分方程式がベッセルの微分方程式で、円筒形の対称性を持つ物理問題でしばしば現れる重要な微分方程式である。特に振動現象や波動の解析に広く応用されている。
ベッセル微分方程式は、パラメータを\(\nu\)とすると式(2)で表せる。$$t^2\frac{d^2x}{dt^2}+ t\frac{dx}{dt} +(t^2 - \nu^2)x=0 \;\;\; \cdots(2)$$ここで、\(t\) は独立変数、\(\nu\)は次数（実数または複素数）、\(x(t)\)は解となる関数である。特異点は\(t=0,\;t=\infty\)の２つである。そして\(x=0\)のみが確定特異点になっている。
ベッセルの微分方程式 式(2)を\(x=0\)でのべき展開で解く。$$x=\sum_{n=0}^\infty \alpha_n t^{\rho +n}$$これを式(2)に代入すると、式(3)となる。$$\sum_{n=0}^\infty \left\{(\rho + n)(\rho + n-1) + (\rho + n) - \nu^2\right\}\alpha_n t^{\rho +n} + \sum_{n=0}^\infty \alpha_n t^{\rho +n +2} = 0 \;\;\; \cdots (3)$$式(3)を整理すると$$\sum_{n=0}^\infty \left\{(\rho+n)^2 - \nu^2\right\}\alpha_n t^n + \sum_{n=2}^\infty \alpha_{n-2} t^n =0 \;\;\; \cdots (4)$$となる。従って、$$(\rho^2 - \nu^2)\alpha_0 = 0 \;\;(\alpha_0 \neq 0) \\ \left\{(\rho+1)^2 - \nu^2\right\}\alpha_1 = 0 \\ \left\{(\rho+n)^2 - \nu^2\right\}\alpha_n + \alpha_{n-2} = 0\;\;(n=2,3,\cdots) \;\;\; \cdots (5)$$でなければならない。式(5)の第１式は決定方程式で、その解は、\(\rho = \nu,\;\rho=-\nu\)である。
\(\rho = \nu\)の場合、式(5)の第２式、第３式は、$$(2 \nu +1)\alpha_1 = 0 \\ n(2\nu +n)\alpha_n = -\alpha_{n-2} \;\; (n=2,3,\cdots) \;\;\; \cdots (6)$$となる。式(6)の第１式から\(\nu \neq -1/2\)である限り、\(\alpha_1=0\)である。これを第２式に代入すると\(n\)が奇数ならば\(\alpha_n = 0\)である。つまり\(n\)が偶数の場合だけが残る。従って、\(n=2m\)とおくと、式(6)の第２式は\(\nu\)が負の整数でなければ、$$\alpha_{2m}=-\frac{\alpha_{2m-2}}{2m(2\nu +2m)}=\frac{-\alpha_{2(m-1)}}{2^2 m(\nu +m)}$$となる。よって、$$\alpha_{2m} = \frac{(-1)^m \alpha_0}{2^{2m} m! (\nu +1)_m}$$が求まる。これより解は、$$x_1=\alpha_0 \sum_{m=0}^\infty \frac{(-1)^m}{2^{2m}m!(\nu +1)_m}t^{\nu+2m} \;\;\; \cdots (7)$$である。
なお、\(\nu =1/2\)のときは、\(t^2\frac{d^2x}{dt^2}+ t\frac{dx}{dt} +(t^2 - 1/4)x=0\)となり、 \(x=v/\sqrt{t}\)と変数変換すると$$\frac{dx}{dt} = t^{-\frac{1}{2}}\frac{dv}{dt} - t^{-\frac{3}{2}}\frac{v}{2} \\ \frac{d^2 x}{dt^2} = t^{-\frac{1}{2}} \frac{d^2 v}{dt^2} - t^{-\frac{3}{2}}\frac{3}{2} \frac{dv}{dt} + t^{-\frac{5}{2}}\frac{3}{4}v$$なので、これらを代入すると、$$t^2\frac{d^2x}{dt^2}+ t\frac{dx}{dt} +\left(t^2 - \frac{1}{4}\right)x \\ = t^2\left( t^{-\frac{1}{2}} \frac{d^2 v}{dt^2} - t^{-\frac{3}{2}}\frac{3}{2} \frac{dv}{dt} + t^{-\frac{5}{2}}\frac{3}{4}v\right) + t \left(t^{-\frac{1}{2}}\frac{dv}{dt} - t^{-\frac{3}{2}}\frac{v}{2}\right) + \left(t^2 - \frac{1}{4}\right)t^{-\frac{1}{2}}v \\ =t^{\frac{3}{2}} \left(\frac{d^2 v}{dt^2} + v\right)=0$$ よって、$$ \frac{d^2 v}{dt^2} + v =0$$となる。これは単振動の微分方程式であり、一般解は$$v(t) = A \cos(t) + B\sin(t)$$ (A, B は任意定数)である。よって、元の変数\( x\) についての解は$$x(t) = \frac{1}{\sqrt{t}}(A \cos(t) + B\sin(t))$$の三角関数で表せる。
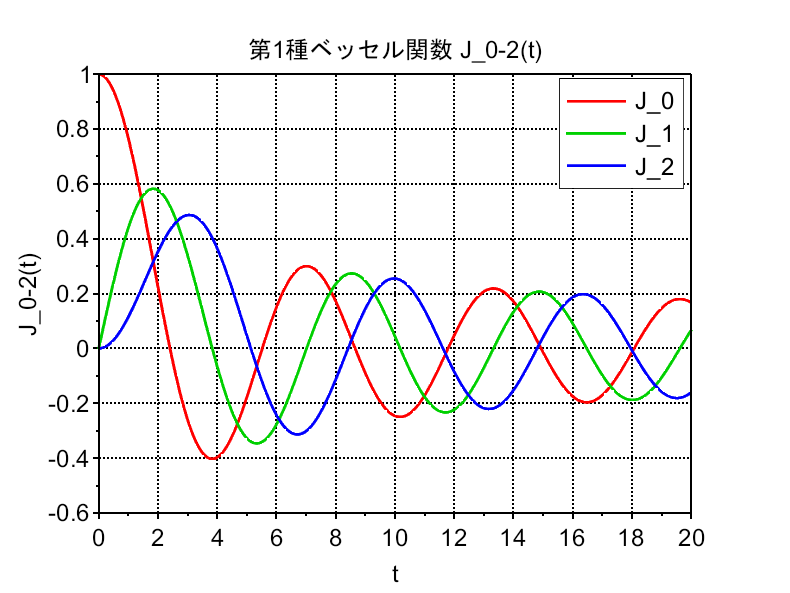
式(7)で\(\alpha_0=\frac{2^{-\nu}}{\Gamma(\nu +1)}\)とおいたものを、「第１種ベッセル関数」といい、式(8)のように書く。$$J_\nu (t)=\sum_{m=0}^\infty \frac{(-1)^m}{m! \Gamma(\nu + m+1)}\left(\frac{t}{2}\right)^{\nu + 2m} \;\;\; \cdots (8)$$ここで、\(\rho=-\nu\)の解は、式(8)の\(\nu\)を\(-\nu\)に変えた式で与えられる。
式(8)から、次の関係式が得られる。$$\frac{d}{dt}\left(t^{-\nu}J_\nu (t)\right)= -t^{-\nu}J_{\nu +1}(t)\\ \frac{d}{dt}\left(t^\nu J_\nu (t) \right)=t^\nu J_{\nu-1}(t)$$次に\(\nu\)が整数の場合、\(\nu\)が０または正の整数\(n\)ならば、式(8)から、$$J_n(t)=\sum_{m=0}^\infty \frac{(-1)^m}{m! (n+m)!}\left(\frac{t}{2}\right)^{n+2m}$$である。\(\nu\)が負の整数\(-n\)の場合は、\(\frac{1}{\Gamma(-n+m+1)}\)が\(m \lt n\)のとき0なので、和は\(m=n\)から始まるので$$J_{-n}(t) = \sum_{m=n}^\infty \frac{(-1)^m}{m! (m-n)!}\left(\frac{t}{2}\right)^{-n+2m}$$である。さらに、\(m-n=k\)と書き換えると$$J_{-n}(t) = \sum_{k=0}^\infty \frac{(-1)^{n+k}}{(n+k)!k!}\left(\frac{t}{2}\right)^{n+2k}$$なので、$$J_{-n}(t) = (-1)^n J_n(t)$$である。
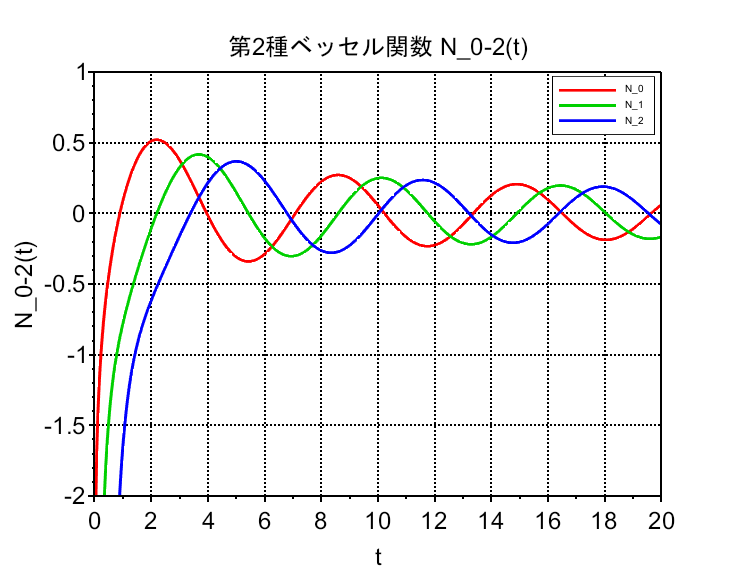
\(\nu\)が整数の場合も含めて第１種ベッセル関数と独立な「第２種ベッセル関数（ノイマン関数）」を$$N_\nu(t) =\frac{\cos(\nu \pi) J_\nu(t) - J_{-\nu}(t)}{\sin(\nu \pi)}$$で定義する。\(J_\nu(t)\)とは独立な解であり、原点\(t=0\)で特異点を持ち無限大に発散する。振動的な挙動を持ち、特に大きい\(t\)に対しては \(J_\nu(t)\)と同様に振る舞う。用途として、\(t=0\)を含まない物理問題、または境界条件が特異性を有す場合に使用される。\(J_\nu(t)\) 及び \(N_\nu(t)\)はどちらも、負の実軸を除く複素平面上で \(t\)の解析的な関数（正則な関数）である。\(\nu\)が正の整数のとき、これらの関数は負の実軸上に分岐点を持たず、したがって\( t\)の整関数となる。また、固定した \(t\)に対してベッセル関数は \(\nu\)の整関数となる。

ラゲールの微分方程式

ベッセルの微分方程式と似ていて、より簡単な微分方程式が、式(9)に示すラゲールの微分方程式である。$$tx'' + (1-t)x' + \nu x=0 \;\;\; \cdots (9)$$ $$x = \sum_{n=0}^\infty \alpha_n t^{\rho + n}$$として、式(9)に代入すると、$$t^\rho \sum_{n=0}^\infty \left\{(\rho +n)^2 \alpha_n t^{n-1} + (-\rho -n +\nu)\alpha_n t^n\right\}=0$$となる。よって、決定方程式は、\(\rho^2=0\)となる。\(\rho=0\)なので、\(n \geq 1\)に対して$$n^2 \alpha_n + \left\{-(n-1)+\nu\right\}\alpha_{n-1}=0$$であるから、\(\alpha_0 = 1\)とすると、$$\alpha_n = \frac{(-\nu)_n}{(n!)^2}$$となる。よって、特殊解は$$x = \sum_{n=0}^\infty \frac{(-\nu)_n}{(n!)^2}t^n \;\;\; \cdots (10)$$である。

ラゲール多項式

式(10)は、\(\nu=0,1,2,\cdots\)ならば有限次となり、式(11)の\(n\)次の多項式、ラゲール多項式となる。$$L_n(t) = \sum_{k=0}^n \frac{(-1)^k n!}{(n-k)!(k!)^2}t^k \;\;\; \cdots (11)$$ラゲール多項式は、ラゲールの微分方程式 式(9)を満たす。すなわち、$$t L_n''(t) + (1-t)L_n'(t) + n L_n(t)=0 \;\;\; \cdots (12)$$である。
式(11)から$$tL_n'(t) = \sum_{k=0}^n k\cdot \frac{(-1)^k n!}{(n-k)!(k!)^2} t^k \;\;\;\cdots (13)$$となるが、\(k=n-(n-k)\)と書き換えると、式(13)の右辺は、\(nL_n - nL_{n-1}\)に等しい。よって、$$tL_n'(t)= n\left\{L_n(t) - L_{n-1}(t)\right\} \;\;\;\cdots (14)$$である。これを微分すると$$L_n'(t)+tL_n''(t) = n\left\{L_n'(t) - L_{n-1}'(t)\right\}$$となり、これを式(12)に代入し整理すると$$-tL_n'(t)+n\left\{L_n'(t)+L_n(t)-L_{n-1}'(t)\right\}=0$$となる。この第１項に式(14)を代入すると$$L_n'(t)+L_{n-1}(t)-L_{n-1}'(t)=0$$となる。これに\(t\)を乗じて再度 式(14)を代入して整理すると式(15)の漸化式が得られる。$$nL_n(t)=(2n-1-t)L_{n-1}(t) -(n-1)L_{n-2}(t) \;\;\;\cdots (15)$$

参考

特殊関数のグラフを作成しようかと考えたが、下記の優れたサイトを見つけたので、それを紹介することでグラフは省略する。
＊URL：http://math-functions-1.watson.jp、サイトの管理者：Souichiro Ikebe