19. 偏微分方程式（微分方程式）

偏微分方程（Partial Differential Equation, PDE）は、複数の独立変数に依存する未知関数とその偏導関数を含む方程式である。これは、物理学、工学、生物学、経済学など、多くの分野で自然現象やシステムの挙動を記述するために広く用いられる。常微分方程式では独立変数が１個であるが、例えば、時間と空間の両方を独立変数とすると偏微分方程式での取り扱いとなる。また、時間変化がない静的な問題であっても、対象が点でなく、広がった物体や波動、さらに場を取り扱う場合には３次元空間を表す３つの座標を独立変数にしなければならないので、偏微分方程式が必要である。
偏微分方程式は、未知関数の偏導関数を含む方程式なので、式(1)の一般形で表される。$$F\left( x_1,x_2,\ldots,x_n, u, \frac{\partial u}{\partial x_1}, \frac{\partial u}{\partial x_2}, \ldots,\frac{\partial^2 u}{\partial x_1 \partial x_2}, \ldots \right) = 0 \;\;\; \cdots (1)$$ここで、\(x_1,x_2 ,\ldots,x_n\)は独立変数、\(u\)は未知関数、\(\partial u / \partial x_1\)などは\(u\)の偏導関数である。偏微分方程式の階数は、方程式中に現れる最高次の偏導関数の階数によって決まる。例えば、二階の偏導関数が含まれる場合、その方程式を二階偏微分方程式と呼ぶ。
偏微分方程式の簡単な例は、\(x,\;y\)を独立変数、\(f(x,y)\)を既知関数、\(\Phi(x,y)\)を未知関数とするとき、$$\frac{\partial \Phi(x,y)}{\partial x}=f(x,y) \;\;\;\cdots (2)$$で、その解は、$$\Phi(x,y) = \int f(x,y)dx \;\;\; \cdots(3)$$ である。「偏積分」という記号はなく、式(3)の\(x\)積分は、\(y\)を定数と考えてする積分となる。従って、不定積分に含まれる任意定数は、\(y\)の任意関数となる。一般に\(n\)個の独立変数をもつ偏微分方程式の一般解は、\(n-1\)個の独立変数をもつ任意関数を含むことになる。偏微分方程式で現れる任意関数を固定するには、常微分方程式の場合と同様で、初期条件、または、境界条件を与えることでなされる。特定の初期条件や境界条件の下で偏微分方程式の解を求める問題をコーシー問題という。コーシー問題では、ある偏微分方程式に対して、定義域内の特定の超曲面上で与えられた初期条件を満たす解を求める。具体的には、\(n\)次元空間内の偏微分方程式と、\(n−1\)次元の滑らかな多様体（コーシー曲面）上での初期条件が与えられ、その条件を満たす未知関数を見つけることが目的となる。
偏微分方程式を考える際に気を付けることは、独立変数は個々ではなく、必ずセットで認識しなければならないことである。すなわち、\((x,\;y)\)という独立変数の系で、\(y\)のみを\(\hat{y}\)に変数変換したときでも、新しい独立変数の系は\((\hat{x},\;\hat{y})\)である。偏微分の変換は一般に$$\frac{\partial}{\partial x} = \frac{\partial \hat{x}}{\partial x}\frac{\partial}{\partial \hat{x}} + \frac{\partial \hat{y}}{\partial x}\frac{\partial}{\partial \hat{y}} \\ \frac{\partial}{\partial y} = \frac{\partial \hat{x}}{\partial y}\frac{\partial}{\partial \hat{x}} + \frac{\partial \hat{y}}{\partial y}\frac{\partial}{\partial \hat{y}}$$なので、変換において\(x=\hat{x}\)であっても、\(\hat{y}\)が\(x\)に依存してる限り、\(\frac{\partial}{\partial x}=\frac{\partial}{\partial \hat{x}}\)とはならない。

２階同次線形偏微分方程式

偏導関数の係数が定数の場合の同次線形偏微分方程式を考える。独立変数が２個の場合の１階偏微分方程式は、式(4)で表せる。$$a\frac{\partial \Phi}{\partial x} + b\frac{\partial \Phi}{\partial y} +f(x,y)\Phi =0 \;\;\; \cdots (4)$$ この式で、\(\hat{x}=x/a,\;\; \hat{y}=(x/a)-(y/b)\)と変数変換する。これは、\(x=a \hat{x} ,\;\; y=b\hat{x} - b \hat{y}\)である。次に元の偏微分を新しい変数に関する偏微分に変換する。$$\frac{\partial \Phi}{\partial x} = \frac{\partial \Phi}{\partial \hat{x}} \frac{\partial \hat{x}}{\partial x} + \frac{\partial \Phi}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial x} ,\;\;\;\; \frac{\partial \Phi}{\partial y} = \frac{\partial \Phi}{\partial \hat{x}} \frac{\partial \hat{x}}{\partial y} + \frac{\partial \Phi}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial y}$$これらの偏微分を計算すると$$\frac{\partial \hat{x}}{\partial x} = \frac{1}{a}, \quad \frac{\partial \hat{x}}{\partial y} = 0, \quad \frac{\partial \hat{y}}{\partial x} = \frac{1}{a}, \quad \frac{\partial \hat{y}}{\partial y} = -\frac{1}{b}$$​従って、$$\frac{\partial \Phi}{\partial x} = \frac{1}{a} \frac{\partial \Phi}{\partial \hat{x}} + \frac{1}{a} \frac{\partial \Phi}{\partial \hat{y}} ,\quad \frac{\partial \Phi}{\partial y} = -\frac{1}{b} \frac{\partial \Phi}{\partial \hat{y}}$$​これらを元の方程式に代入すると、$$a\left(\frac{1}{a} \frac{\partial \Phi}{\partial \hat{x}} + \frac{1}{a} \frac{\partial \Phi}{\partial \hat{y}}\right) + b\left(-\frac{1}{b} \frac{\partial \Phi}{\partial \hat{y}}\right) + f(x,y)\Phi = 0$$これを簡略化すると$$\frac{\partial \Phi}{\partial \hat{x}} + \frac{\partial \Phi}{\partial \hat{y}} - \frac{\partial \Phi}{\partial \hat{y}} + f(x,y)\Phi = 0 ,\quad \frac{\partial \Phi}{\partial \hat{x}} + f(x,y)\Phi = 0$$となる。また、\(f(x,y)\) を新しい変数で表現する。元の変数\(x\)と\(y\) を新しい変数で表すと、$$x = a\hat{x}, \quad y = b(\hat{x} - \hat{y})$$したがって、\(f(x,y)\)は \(f(a\hat{x}, b(\hat{x} - \hat{y}))\)と表せ、これを\(\hat{f}(\hat{x},\hat{y})\)とする。以上より、変数変換後の偏微分方程式は式(5)となる。$$\frac{\partial \Phi}{\partial \hat{x}} + \hat{f}(\hat{x}, \hat{y})\Phi= 0 \;\;\; \cdots(5)$$さらに、式(5)で\(\Phi = e^{-\Phi}\)とおくと、$$\frac{\partial \Phi}{\partial \hat{x}} = \frac{\partial}{\partial \hat{x}}e^{-\Phi} = -e^{-\Phi}\frac{\partial \Phi}{\partial \hat{x}} = -\Phi\frac{\partial \Phi}{\partial \hat{x}}$$ これを元の方程式に代入すると$$-\Phi \frac{\partial \Psi}{\partial \hat{x}} + \hat{f}(\hat{x},\hat{y})\Phi = 0$$よって、$$\Phi \frac{\partial \Psi}{\partial \hat{x}} = \hat{f}(\hat{x},\hat{y})\Phi , \quad \frac{\partial \Psi}{\partial \hat{x}} = \hat{f}(\hat{x},\hat{y})$$となり、式(2)に帰着する。以上のように変数変換は、偏微分方程式の解法において強力な手法であり、特に方程式の形状を簡略化する際に有効である。
２階偏微分方程式の場合も同様に、適当な１次変換で式(6)の３つの標準形のどれかで表せる。$$\frac{\partial^2 \Phi}{\partial x^2} +\frac{\partial ^2 \Phi}{\partial y^2} +f(x,y)\Phi =0 \\ \frac{\partial^2 \Phi}{\partial x^2} - \frac{\partial ^2 \Phi}{\partial y^2} +f(x,y)\Phi =0 \\ \frac{\partial^2 \Phi}{\partial x^2} -\frac{\partial \Phi}{\partial y} +f(x,y)\Phi =0 \;\;\; \cdots (6)$$ 具体例としては、以下がある。
・ラプラス方程式：電場や重力場のポテンシャルのような調和関数を記述する。$$\frac{\partial^2 \Phi}{\partial x^2} + \frac{\partial^2 \Phi}{\partial y^2} = 0$$
・波動方程式：時間と空間における波の伝播を示す。$$\frac{\partial^2 \Phi}{\partial t^2} = c^2 \frac{\partial^2 \Phi}{\partial x^2}$$ここで、\(c\)は波の速度。
・熱方程式：時間と空間における温度の変化を示す。$$\frac{\partial \Phi}{\partial t} = \alpha \frac{\partial^2 \Phi}{\partial x^2}$$ここで、\(\alpha\)は熱拡散率。

ラプラシアン

ラプラシアンは、数学や物理学において重要な微分作用素であり、関数の各変数に関する二階偏導関数の和として定義される。これは、関数の曲率や変化の度合いを解析する際に用いられる。直交座標系において、スカラー関数 \(f(x, y, z)\)のラプラシアンは次のように定義される。$$\Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}\;\;\; \cdots (7)$$これは、関数 \(f\)の各変数に関する二階偏導関数を合計したものである。ラプラシアンは、関数の勾配（各変数に関する一階偏導関数のベクトル）の発散（ダイバージェンス）としても表現できる。つまり、ラプラシアンは関数の変化の度合いを示す指標であり、特に関数がどの程度平坦であるか、あるいはどの程度急激に変化しているかを表現する。式(6)の第１式で\(f \equiv 0\)とした方程式をラプラスの微分方程式という。２次元の場合は式(8)となる。$$\Delta \Phi =\left(\frac{\partial^2}{\partial x^2} +\frac{\partial^2}{\partial y^2}\right)\Phi =0 \;\;\; \cdots (8)$$ ここで\(\Delta\)が２次元ラプラシアンである。
\(f(x,y)\)がある場合、すなわち$$(\Delta +f(x,y))\Phi= 0 \;\;\; \cdots (9)$$は一般には解けない。しかし、\(f(x,y)\)が特別な形の場合、例えば、\(x\)のみの関数と\(y\)のみの関数との和になっている場合は、常微分方程式に帰着させられる。
\(f(x,y)=g(x)+h(y)\)のとき、\(\Phi(x,y)=\phi(x) \varphi(y)\)とおくと、式(9)は、$$\frac{1}{\phi(x)}\left(\frac{\partial^2}{\partial x^2} +g(x)\right)\phi(x)= - \frac{1}{\varphi(y)}\left(\frac{\partial^2}{\partial y^2} +h(y)\right)\varphi(y)$$と書ける。左辺は\(x\)のみの関数、右辺は\(y\)のみの関数であるので、等しいためには定数でなくてはならない。この定数を\(\lambda\)とおくと、$$\frac{1}{\phi(x)}\left(\frac{\partial^2}{\partial x^2} +g(x)\right)\phi(x)=\lambda\quad \Rightarrow \quad \left(\frac{d^2}{dx^2} + g(x) - \lambda\right)\phi(x)=0$$ $$- \frac{1}{\varphi(y)}\left(\frac{\partial^2}{\partial y^2} +h(y)\right)\varphi(y)=\lambda \quad \Rightarrow \quad \left(\frac{d^2}{dy^2} + h(y) + \lambda\right)\varphi(y)=0$$このように常微分方程式で表せる。

２次元ラプラシアンの極座標変換

ラプラシアンは何次元でも座標回転で不変である。微分演算子をラプラシアンでのみ含む偏微分方程式は、極座標に変換すると便利なことが多い。
２次元の極座標\((r,\;\theta)\)と直交座標の関係は、\(x=r \cos \theta,\; y = r \sin \theta\)、もしくは、\(r=\sqrt{x^2 + y^2},\;\theta = \tan^{-1}(y/x)\)である。これらより、$$\frac{\partial r}{\partial x}=\frac{\partial \sqrt{x^2 + y^2}}{\partial x} = \frac{1}{2\sqrt{x^2+y^2}}\cdot 2x = \frac{x}{r} = \cos \theta$$となり、以下同様にして、$$\frac{\partial \theta}{\partial x}= -\frac{y}{r^2} = -\frac{\sin \theta}{r} ,\quad \frac{\partial r}{\partial y}=\frac{y}{r} = \sin \theta,\quad \frac{\partial \theta}{\partial y} = \frac{x}{r^2} = \frac{\cos \theta}{r}$$である。よって、$$\frac{\partial}{\partial x} = \frac{\partial r}{\partial x}\frac{\partial}{\partial r} +\frac{\partial \theta}{\partial x}\frac{\partial}{\partial \theta}=\cos\theta \frac{\partial}{\partial r} -\frac{\sin \theta}{r}\frac{\partial}{\partial \theta} \\ \frac{\partial}{\partial y} = \frac{\partial r}{\partial y}\frac{\partial}{\partial r} +\frac{\partial \theta}{\partial y}\frac{\partial}{\partial \theta}=\sin\theta \frac{\partial}{\partial r} +\frac{\cos \theta}{r}\frac{\partial}{\partial \theta}$$を得る。オイラーの公式より、$$\frac{\partial}{\partial x} \pm j \frac{\partial}{\partial y} = e^{\pm j\theta}\left(\frac{\partial}{\partial r} \pm \frac{j}{r} \frac{\partial}{\partial \theta}\right)$$であるので、$$\Delta = \left(\frac{\partial}{\partial x} -j \frac{\partial}{\partial y}\right)\left(\frac{\partial}{\partial x} + j\frac{\partial}{\partial y}\right)\\= e^{- j\theta}\left(\frac{\partial}{\partial r} - \frac{j}{r} \frac{\partial}{\partial \theta}\right) e^{j\theta}\left(\frac{\partial}{\partial r} + \frac{j}{r} \frac{\partial}{\partial \theta}\right) \;\;\; \cdots (10)$$となる。ここで、ある関数\(f(r,\theta)\)に作用させることを考えると、$$e^{-j\theta}\frac{\partial f e^{j\theta}}{\partial \theta} = e^{-j\theta}\left(\frac{\partial f}{\partial \theta}e^{j\theta} + f je^{j\theta}\right) = \frac{\partial f}{\partial \theta} + f j$$となるので、$$e^{-j\theta}\frac{\partial}{\partial \theta}e^{j \theta} = \frac{\partial}{\partial \theta}+ j$$と書ける。以下このように関数\(f(r,\theta)\)に作用させることを念頭に、積の微分と複素数の性質を繰り返し適用して式(10)を展開する。$$e^{- j\theta}\left(\frac{\partial}{\partial r} - \frac{j}{r} \frac{\partial}{\partial \theta}\right) e^{j\theta}\left(\frac{\partial}{\partial r} + \frac{j}{r} \frac{\partial}{\partial \theta}\right) \\ = e^{-j\theta}\left(\frac{\partial}{\partial r} - \frac{j}{r}\frac{\partial}{\partial \theta}\right)\left(e^{j\theta}\frac{\partial}{\partial r} + \frac{j}{r} e^{j\theta}\frac{\partial}{\partial \theta}\right) \\ =e^{-j\theta}\frac{\partial}{\partial r}\left(e^{j \theta}\frac{\partial}{\partial r}\right) + e^{-j \theta}\frac{\partial}{\partial r}\left(\frac{j}{r}e^{j \theta}\frac{\partial}{\partial \theta}\right) - \frac{j}{r}e^{-j \theta}\frac{\partial}{\partial \theta}\left(e^{j\theta}\frac{\partial}{\partial r}\right) - \frac{j}{r}e^{-j \theta}\frac{\partial}{\partial \theta}\left(\frac{j}{r}e^{j\theta}\frac{\partial}{\partial \theta}\right) \\ = \frac{\partial^2}{\partial r^2} - \frac{j}{r^2}\frac{\partial}{\partial \theta} + \frac{j}{r}\frac{\partial^2}{\partial r \partial \theta} + \frac{1}{r}\frac{\partial}{\partial r} - \frac{j}{r}\frac{\partial^2}{\partial \theta \partial r} + \frac{j}{r^2}\frac{\partial}{\partial \theta} + \frac{1}{r^2}\frac{\partial^2}{\partial \theta^2} \\ = \frac{\partial^2}{\partial r^2} +\frac{1}{r}\frac{\partial}{\partial r} +\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}$$この計算の結果より、２次元ラプラシアンは極座標で式(11)である。$$\Delta = \frac{\partial^2}{\partial r^2} +\frac{1}{r}\frac{\partial}{\partial r} +\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2} \;\;\; \cdots (11)$$
※https://w3e.kanazawa-it.ac.jp/math/category/bibun/henbibun/henkan-tex.cgi?target=/math/category/bibun/henbibun/rapurashian-2_1.htmlも参考になるが、軽微な記載ミスがある。導出法、結果に問題はないと思う。

３次元ラプラシアンの極座標変換

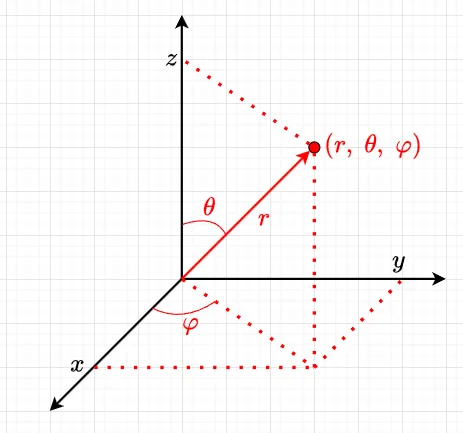
３次元ラプラシアンを極座標に変換した結果は式(13)となる。$$\Delta = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2 \frac{\partial}{\partial r}\right) + \frac{1}{r^2 \sin \theta}\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right) + \frac{1}{r^2 \sin^2\theta}\frac{\partial^2}{\partial \varphi^2} \;\;\; \cdots(13)$$

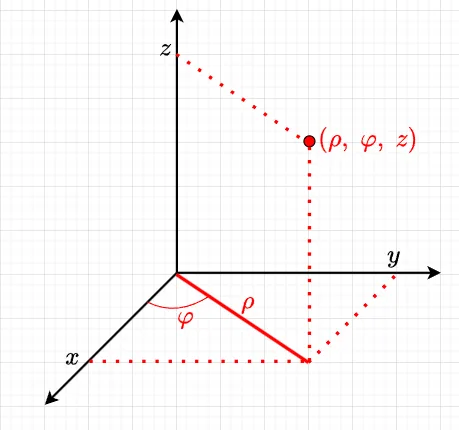
次に\(\rho = r\sin\theta,\;z = r\cos\theta\)という変数変換を行う。式(14)において、第１項と第４項の和は２次元のラプラシアンなので、式(11)を使って$$ \frac{\partial^2}{\partial \rho^2} +\frac{\partial^2}{\partial z^2} =\frac{\partial^2}{\partial r^2} +\frac{1}{r}\frac{\partial}{\partial r} +\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}$$となる。次に、２次元ラプラシアンの極座標変換における$$\frac{\partial}{\partial y} = \frac{\partial r}{\partial y}\frac{\partial}{\partial r} +\frac{\partial \theta}{\partial y}\frac{\partial}{\partial \theta}=\sin\theta \frac{\partial}{\partial r} +\frac{\cos \theta}{r}\frac{\partial}{\partial \theta}$$の関係を使って、 $$\frac{1}{\rho}\frac{\partial}{\partial \rho} =\frac{1}{r\sin \theta}\left(\sin\theta \frac{\partial}{\partial r} +\frac{\cos \theta}{r}\frac{\partial}{\partial \theta}\right)=\frac{1}{r}\frac{\partial}{\partial r} +\frac{\cos \theta}{r^2\sin\theta}\frac{\partial}{\partial \theta}$$となる。また、 $$\frac{1}{\rho^2}\frac{\partial^2}{\partial \varphi^2}=\frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial \varphi^2}$$以上より、$$\Delta=\left(\frac{\partial^2}{\partial r^2} +\frac{1}{r}\frac{\partial}{\partial r} +\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}\right) + \left(\frac{1}{r}\frac{\partial}{\partial r} +\frac{\cos \theta}{r^2\sin\theta}\frac{\partial}{\partial \theta}\right) + \frac{1}{r^2\sin^2\theta}\frac{\partial^2}{\partial \varphi^2}$$である。
この前２つの括弧を整理する。$$\left(\frac{\partial^2}{\partial r^2} +\frac{1}{r}\frac{\partial}{\partial r}\right) + \left(\frac{1}{r}\frac{\partial}{\partial r}\right) = \frac{\partial^2}{\partial r^2} + \frac{2}{r}\frac{\partial}{\partial r}= \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2 \frac{\partial}{\partial r}\right)$$また、$$\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2} + \frac{\cos \theta}{r^2\sin\theta}\frac{\partial}{\partial \theta} = \frac{1}{r^2} \left( \frac{\partial^2}{\partial \theta^2} + \frac{\cos \theta}{\sin\theta}\frac{\partial}{\partial \theta} \right)$$ ここで、$$\frac{\cos \theta}{\sin\theta} = \frac{d}{d\theta} \left( \ln|\sin\theta| \right)$$従って、$$\frac{1}{r^2} \left( \frac{\partial^2}{\partial \theta^2} + \frac{\cos \theta}{\sin\theta}\frac{\partial}{\partial \theta} \right) = \frac{1}{r^2} \left( \frac{\partial^2}{\partial \theta^2} + \frac{d}{d\theta} \left( \ln|\sin\theta| \right) \frac{\partial}{\partial \theta} \right)$$ 括弧内は、$$\frac{\partial^2}{\partial \theta^2} + \frac{d}{d\theta} \left( \ln|\sin\theta| \right) \frac{\partial}{\partial \theta} = \frac{1}{\sin\theta} \frac{\partial}{\partial \theta} \left( \sin\theta \frac{\partial}{\partial \theta} \right)$$となる。
よって、$$\frac{1}{r^2} \left( \frac{\partial^2}{\partial \theta^2} + \frac{\cos \theta}{\sin\theta}\frac{\partial}{\partial \theta} \right) = \frac{1}{r^2 \sin \theta}\frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)$$である。以上をまとめると式(13)となる。
※https://w3e.kanazawa-it.ac.jp/math/category/bibun/henbibun/henkan-tex.cgi?target=/math/category/bibun/henbibun/rapurashian-3.htmlは、導出法が異なるが参考になる。

波動方程式

式(6)の第２式、第３式は、\(y\)を時間\(t\)の定数倍と同定すると、時間発展を記述する微分方程式と解釈できる。式(6)の第２式で、\(f(x,y)=0,\;y=vt\)（\(v\)は定数）とすると、$$\left(\frac{\partial^2}{\partial x^2} - \frac{1}{v^2}\frac{\partial^2}{\partial t^2}\right)\Phi(x,t)=0 \;\;\; \cdots (15)$$である。この式より、$$\frac{\partial^2 \Phi}{\partial x^2} - \frac{1}{v^2}\frac{\partial^2 \Phi}{\partial t^2}$$ \(u=x-vt,\; w=x+vt\)で変数変換する。\(\frac{\partial}{\partial x} \) は\(u\)と\(w\)に関して次のように書ける。$$\frac{\partial}{\partial x} = \frac{\partial u}{\partial x} \frac{\partial}{\partial u} + \frac{\partial w}{\partial x} \frac{\partial}{\partial w} = \frac{\partial}{\partial u} + \frac{\partial}{\partial w}$$ \(\frac{\partial}{\partial t}\)も同様にできる。$$\frac{\partial}{\partial t} = \frac{\partial u}{\partial t} \frac{\partial}{\partial u} + \frac{\partial w}{\partial t} \frac{\partial}{\partial w} = -v \frac{\partial}{\partial u} + v \frac{\partial}{\partial w}$$ ​さらに、それぞれの2階微分は、$$\frac{\partial^2}{\partial x^2} = \left( \frac{\partial}{\partial u} + \frac{\partial}{\partial w} \right)^2 = \frac{\partial^2}{\partial u^2} + 2\frac{\partial^2}{\partial u \partial w} + \frac{\partial^2}{\partial w^2}$$ $$\frac{\partial^2}{\partial t^2} = \left( -v \frac{\partial}{\partial u} + v \frac{\partial}{\partial w} \right)^2 = v^2 \frac{\partial^2}{\partial u^2} - 2v^2 \frac{\partial^2}{\partial u \partial w} + v^2 \frac{\partial^2}{\partial w^2}$$​となる。これを波動方程式に適用する。$$\frac{\partial^2 \Phi}{\partial x^2} - \frac{1}{v^2} \frac{\partial^2 \Phi}{\partial t^2} = \left( \frac{\partial^2}{\partial u^2} + 2\frac{\partial^2}{\partial u \partial w} + \frac{\partial^2}{\partial w^2} \right) \Phi - \left( \frac{\partial^2}{\partial u^2} - 2\frac{\partial^2}{\partial u \partial w} + \frac{\partial^2}{\partial w^2} \right) \Phi = 4\frac{\partial^2 \Phi}{\partial u \partial w}$$従って、波動方程式は次の形になる。$$\frac{\partial^2 \Phi}{\partial u \partial w} = 0$$を解くと、\(\Phi\)は次のように表せる。$$\Phi(u, w) = f(u) + g(w)$$ここで、\(f(u)\)と\(g(w)\)は任意の2回微分可能な関数である。\(u = x - vt,\;w = x + vt\) を元に戻すと、式(15)の一般解は、$$\Phi(x,t) = f(x-vt)+g(x+vt)$$で与えられる。ここで、\(f(x - vt)\)は右向きに進む一次元の波、\(g(x + vt)\)は左向きに進む一次元の波を表す。なお、関数形は初期条件で決まる。
空間が３次元であると、波動方程式は式(16)となる。$$\left(\Delta - \frac{1}{v^2}\frac{\partial^2}{\partial t^2}\right)\Phi(x,y,z,t)=0 \;\;\; \cdots (16)$$これは、ダランベール方程式と呼ばれ、電磁波の伝播を記述する。3次元のダランベール方程式の解は、一次元の場合とは異なり、球対称な波動の伝播を含む。

熱方程式

式(6)の第３式$$\frac{\partial^2 \Phi}{\partial x^2} -\frac{\partial \Phi}{\partial y} +f(x,y)\Phi =0$$において、\(f=0\)のとき、熱方程式と呼ばれ、熱伝導を記述する。３次元では式(17)となる。$$\frac{\partial \Phi(x,y,z,t)}{\partial t} = \Delta \Phi(x,y,z,t) \;\;\; \cdots (17)$$ この一般解は、初期条件、境界条件によって大きく変化する。また、3次元熱方程式の解法は、方程式の複雑さと境界条件の性質によって大きく異なる。解析解が得られるケースは限られており、多くの場合は数値解法に頼ることになる。