2. \(H_\infty\)制御問題の定式化
\(H_\infty\)制御問題は、適当に定義された外乱\(w\)と制御量\(z\)の間の閉ループ伝達関数\(G_{zw}(s)\)に対して、$$\|G_{zw}\|_\infty \lt \gamma$$として、閉ループ系を安定にする制御器\(C(s)\)(\(H_\infty\)制御器)を求める問題である。この制御器の計算のために一般化プラントを求める。図1のように外乱\(w\)、制御量\(z\)、操作量\(u\)、観測量\(y\)を\(H_\infty\)ノルムを評価する伝達関数\(G(s)\)の両端に設定する。
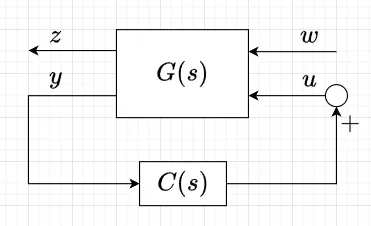
\(C=0\)としたときの入出力の関係、$$\begin{bmatrix} z\\ y\end{bmatrix} = G(s) \begin{bmatrix} w \\ u\end{bmatrix} , \quad G(s) = \begin{bmatrix} G_{11}(s) & G_{12}(s) \\ G_{21}(s) & G_{22}(s)\end{bmatrix}$$を求める。システム行列\(A\)は共通なので、\(G_{ij}\)は、$$G_{11}(s) = C_1(sI-A)^{-1}B_1 + D_{11} \\ G_{12}(s) = C_1(sI -A)^{-1} B_2 + D_{12} \\ G_{21}(s) = C_2 (sI -A)^{-1} B_1 + D_{21} \\ G_{22}(s) = C_2(sI -A)^{-1} B_2 + D_{22}$$とする。この関係を状態方程式と2つの出力方程式で表す。$$\dot{x} = Ax + B_1 w + B_2 u \\ z = C_1 x + D_{11} w + D_{12} u \\ y = C_2 x + D_{21} w + D_{22}u \\ \;\;\; \;\;\;\;\;\;\; \cdots(1)$$ 以上の\(G(s)\)、あるいは、式(1)を一般化プラントという。
この一般化プラントに対して、図1のように制御則を$$u=C(s)y$$ とすると、$$G_{zw}(s) = G_{11} + G_{12} C (I - G_{22} C)^{-1} G_{21}$$と表せる。これに対して、閉ループ系を内部安定にし、\(\|G_{zw}\|_{\infty} \lt \gamma\)を満たす\(H_\infty\)制御器\(C(s)\)を求める。
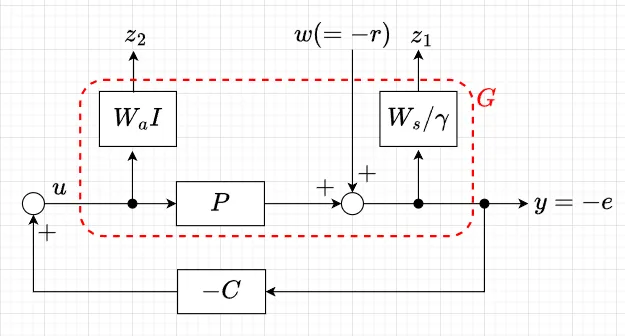
混合感度問題の一般化プラント
混合感度問題では、図2で\(C=0\)とした開ループ系から一般化プラント(赤点線の中)が求まる。$$\begin{bmatrix} z_1 \\ z_2 \\ \hline y \end{bmatrix} = \begin{bmatrix} W_s / \gamma & W_s P/\gamma \\ 0 & W_a I \\ \hline I & P \end{bmatrix} \begin{bmatrix} w \\ u \end{bmatrix}$$となる。
$$P(s) = C_0(sI-A_0)^{-1} B_0 \\ W_s(s)/\gamma = C_s (sI-A_s)^{-1}B_s \\ W_a(s) = C_a(sI-A_a)^{-1}B_a + D_a$$とおくと、図3の状態変数線図となる。状態変数を\(x=[x_s^T ,\; x_T^T ,\; x_a^T]^T\)とおくと、状態方程式で表す一般化プラントは、$$\dot{x} = \begin{bmatrix} A_s & 0 & B_s C_0 \\ 0 & A_a & 0 \\ 0 & 0 & A_0 \end{bmatrix} x + \begin{bmatrix} B_s \\ 0 \\ 0\end{bmatrix} w + \begin{bmatrix} 0 \\ B_a \\ B_0 \end{bmatrix} u \\ z = \begin{bmatrix} C_s & 0 & 0 \\ 0 & C_a & 0 \end{bmatrix} x + \begin{bmatrix} 0 \\ D_a \end{bmatrix} u \\ y = \begin{bmatrix} 0 & 0 & C_0 \end{bmatrix}x + w $$ となる。
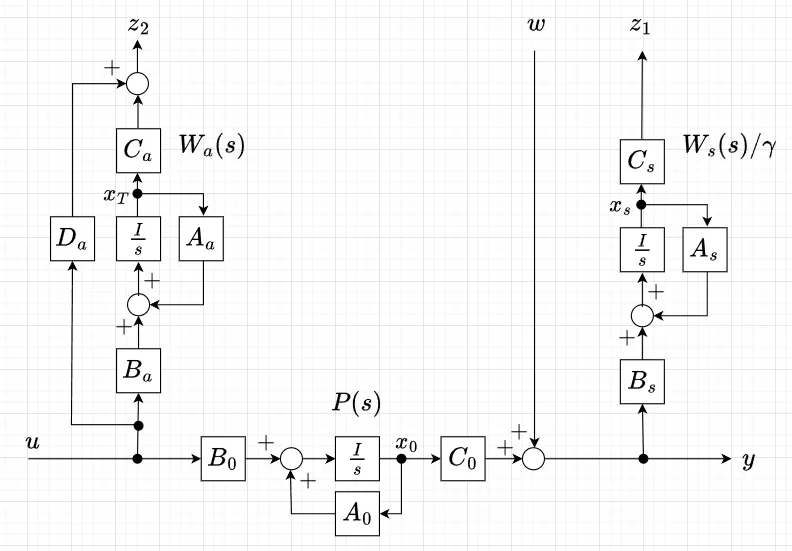
状態変数線図

