3. 制御数学基礎Ⅰ

伝達関数の表現と演算

状態方程式と出力方程式を式(1)とする。$$\dot{x} = Ax + Bu,\quad y=Cx + Du \;\;\; \cdots (1)$$このとき、システムの伝達関数は、式(2)の各種形式で表せる。$$G(s) = C(sI-A)^{-1} B + D , \quad G(s) = (A,B,C,D) , \quad G(s) = \left[\begin{array}{c|c} A & B \\ \hline C & D \end{array}\right] \;\;\; \cdots(2)$$式(2)の表現はドイルの記法と呼ばれる。

伝達関数の操作に関する公式

１．入出力行列の符号に関する不変性　$$\left[\begin{array}{c|c} A & B \\ \hline -C & D \end{array}\right] = \left[\begin{array}{c|c} A & -B \\ \hline C & D \end{array}\right] \;\;\; \cdots (3)$$
２．状態変数の相似変換に対する伝達関数の不変性（\(\text{det}|T| \neq 0\)とする）$$\left[\begin{array}{c|c} T^{-1}AT & T^{-1}B \\ \hline CT & D \end{array}\right] = \left[\begin{array}{c|c} A & B \\ \hline C & D \end{array}\right] \;\;\; \cdots (4)$$
３．伝達関数の転置\(G^T(s)\) $$\left[\begin{array}{c|c} A & B \\ \hline C & D \end{array}\right]^T=\left[\begin{array}{c|c} A^T & C^T \\ \hline B^T & D^T \end{array}\right] \;\;\; \cdots (5)$$
４．伝達関数の共役転置 \(G^{\sim} (s) = G^T(-s) \) $$\left[\begin{array}{c|c} A & B \\ \hline C & D \end{array}\right]^{\sim}=\left[\begin{array}{c|c} -A^T & C^T \\ \hline -B^T & D^T \end{array}\right] \;\;\; \cdots (6)$$
５．伝達関数の逆\(G^{-1}\)（\(D\)が正方で\(\text{\det}|D|\neq 0\)の場合）$$\left[\begin{array}{c|c} A & B \\ \hline C & D \end{array}\right]^{-1} = \left[\begin{array}{c|c} A-BD^{-1}C & BD^{-1} \\ \hline -D^{-1}C & D^{-1} \end{array}\right] \;\;\; \cdots(7)$$
６．伝達関数の並列結合\(G_1 + G_2\)（\(G_1\)と\(G_2\)は同サイズ）$$\left[\begin{array}{c|c} A_1 & B_1 \\ \hline C_1 & D_1 \end{array}\right] + \left[\begin{array}{c|c} A_2 & B_2 \\ \hline C_2 & D_2 \end{array}\right] = \left[\begin{array}{c|c} \begin{array}{c} A_1 & 0 \\ 0 & A_2 \end{array} & \begin{array}{c} B_1 \\ B_2 \end{array} \\ \hline \begin{array}{c} C_1 & C_2 \end{array} & D_1 + D_2 \end{array}\right] \;\;\; \cdots (8)$$
７．伝達関数の直列結合\(G_1 G_2\)（\(G_1\)と\(G_2\)が乗算可能）$$\left[\begin{array}{c|c} A_1 & B_1 \\ \hline C_1 & D_1 \end{array}\right] \times \left[\begin{array}{c|c} A_2 & B_2 \\ \hline C_2 & D_2 \end{array}\right] =\left[\begin{array}{c|c} \begin{array}{c} A_1 & B_1 C_2 \\ 0 & A_2 \end{array} & \begin{array}{c} B_1 D_2 \\ B_2 \end{array} \\ \hline \begin{array}{c} C_1 & D_1 C_2 \end{array} & D_1 D_2 \end{array}\right] = \left[\begin{array}{c|c} \begin{array}{c} A_2 & 0 \\ B_1 C_2 & A_1 \end{array} & \begin{array}{c} B_2 \\ B_1 D_2 \end{array} \\ \hline \begin{array}{c} D_1 C_2 & C_1 \end{array} & D_1 D_2 \end{array}\right] \;\;\; \cdots (9)$$

LFT変換とHM変換

伝達関数として、$$G = \begin{bmatrix} G_{11} & G_{12} \\ G_{21} & G_{22} \end{bmatrix}$$と、\(C\)があるとすると、この\(G\)と\(C\)に対して、式(10)の形式をLFT変換という。$$\text{LFT}(G ,\; C) = G_{11} + G_{12} C(I - G_{22} C)^{-1} G_{21} = G_{11} + G_{12}(I - C G_{22})^{-1} C G_{21} \;\;\; \cdots (10)$$ただし、\(C\)は\(\text{det} |I - G_{22} C | \neq 0\)を満たすと仮定する。

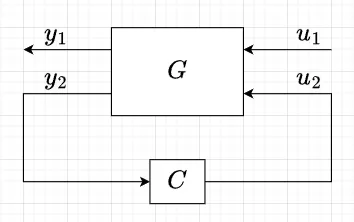
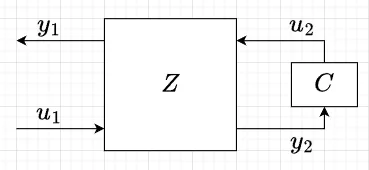
図１を図２のように書き直し、端子間の信号の関係を式(14)で定義する。$$\begin{bmatrix} y_1 \\ u_1 \end{bmatrix} = Z \begin{bmatrix} u_2 \\ y_2 \end{bmatrix} \;\;\; \cdots (14)$$ \(u_2 = C y_2\)なので、$$y_1 = \text{HM}(Z ,\; C)u_1$$を得る。
HM変換の\(Z\)が与えられた場合、$$y_1 = Z_{11} u_2 + Z_{12} y_2,\quad u_1 = Z_{21} u_2 + Z_{22} y_2$$より、$$y_1 = Z_{12} Z_{22}^{-1} u_1 + (Z_{11} - Z_{12} Z_{22}^{-1} Z_{21})u_2$$を得る。よって、
\(\text{det} | Z_{22}| \neq 0\)ならば、LFT変換の\(G\)は、$$G = \begin{bmatrix} Z_{12} Z_{22}^{-1} & Z_{11} - Z_{12}Z_{22}^{-1} Z_{21} \\ Z_{22}^{-1} & -Z_{22}^{-1}Z_{21} \end{bmatrix}$$となる。
また、LFT変換の\(G\)が与えられた場合、\(\text{det}|G_{21}| \neq 0\)ならば、HM変換の\(Z\)は、$$Z = \begin{bmatrix} G_{12} - G_{11} G_{21}^{-1} G_{22} & G_{11} G_{21}^{-1} \\ -G_{21}^{-1} G_{22} & G_{21}^{-1} \end{bmatrix}$$となる。

有理関数の既約分解

有理関数\(G(s)\)は、\(s\)の分母多項式と分子多項式の比で表される関数である。有理関数\(G(s)\)が\(G(\infty) = \text{定数}\)となるときプロパーという。さらに、\(G(\infty) = 0\)となる場合には、厳密にプロパーという。また、\(G(s)\)が安定とは、分母多項式の根（特性根）の実部が負であることである。プロパーで安定な有理関数\(G(s)\)全体を\(RH_{\infty}\)と書く。その単元は分子多項式、分母多項式とも安定でその次数が等しい有理関数となる。
有理行列関数\(W(s)\)は、各要素が安定かつプロパーで\(RH_\infty\)に属する場合、\(W(s) \in RH_\infty\)と記述され、安定行列\(A\)を使って\(W(s) = \{A,B,C,D\}\)で実現される。また、各要素が厳密にプロパーなら\(D=0\)となる。\(W(s) =\{A,B,C,D\} \in RH_\infty\)の場合、\((A,B)\)可安定かつ\((A,C)\)可検出である。また、\(W(s),\;W^{-1}(s) \in RH_\infty\)を満たす正方行列関数\(W(s)\)はユニモジュラと呼ばれる。
同じ列数を持つ行列関数\(R,\;S \in RH_\infty\)が\(R=R'Z,\; S=S'Z\)として右共通因子\(Z \in RH_\infty\)をもつとすると、\(Z\)がユニモジュラ以外にありえない場合、\(R,\;S\)を\(RH_\infty\)上で右既約という。右既約のための必要十分条件は、式(15)のベズー方程式を満たす\(\alpha,\;\beta \in RH_\infty\)が存在することである。$$\alpha R + \beta S = I \;\;\; \cdots (15)$$

既約分解

プロパーなすべての伝達関数\(G(s)\)は右既約な\(M,\;N \in RH_\infty\)を使って式(16)のように\(RH_\infty\)上の右既約分解できる。$$G(s) =NM^{-1} \;\;\; \cdots (16)$$ ここで、\(N,\;M\)は右既約なので、\(\tilde{X},\;\tilde{Y} \in RH_\infty\)が存在して、式(17)が成り立つ。$$\tilde{X} M - \tilde{Y} N = I \;\;\; \cdots(17)$$ また、左既約な\(\tilde{M},\;\tilde{N} \in RH_\infty\)を使って式(18)のように\(RH_\infty\)上の左既約分解できる。$$G(s) = \tilde{M}^{-1} \tilde{N} \;\;\; \cdots(18)$$
［既約分解の例］伝達関数 $$G(s) = \frac{s^3 + 2s^2 + s}{2s^3 + 4s^2 +2s}$$とする。
分子 \(N(s) = s^3 + 2s^2 + s\)、分母 \(M(s) = 2s^3 + 4s^2 +2s\)の最大公約因子は、$$\text{GCD}(N(s),\;M(s)) = s(s+1)$$なので、$$N'(s) = \frac{N(s)}{s(s+1)}=s+1 \\M'(s) = \frac{M(s)}{s(s+1)} = 2(s+1)$$よって、$$G(s) = \frac{N'(s)}{M'(s)}=\frac{s+1}{2(s+1)} =\frac{1}{2}$$となる。

二重既約分解

プロパーなすべての伝達関数\(G(s)\)は、右既約な\(M,\;N \in RH_\infty\)と左既約な\(\tilde{M},\;\tilde{N} \in RH_\infty\)を使って、式(19)のように\(RH_\infty\)上の右既約分解と左既約分解ができる。$$G(s) = N(s) M^{-1}(s) = \tilde{M}^{-1}(s) \tilde{N}(s) \;\;\; \cdots(19)$$このとき、補因子行列\(X,Y, \tilde{X}, \tilde{Y} \in RH_\infty\)が存在し、式(20)が成り立つ。$$\begin{bmatrix} \tilde{X}(s) & - \tilde{Y}(s) \\ -\tilde{N}(s) & \tilde{M}(s) \end{bmatrix} \begin{bmatrix} M(s) & Y(s) \\ N(s) & X(s) \end{bmatrix} = I \;\;\; \cdots (20)$$式(20)が成り立つとき、式(19)を\(G(s)\)の二重既約分解という。
二重既約分解は、制御器を設計する際に、次のような重要な役割を果たす。
１．内部安定性の確保：制御系が内部安定であるためには、システム全体の伝達関数が安定である必要がある。二重既約分解を使用すると、安定性を保ちながら分子・分母を分解できるため、システムの内部安定性を保証する設計が可能になる。
２．\(H_\infty\)制御への応用：\(H_\infty\)制御では、伝達関数を安定に分解して制御器設計を行う。この際、二重既約分解を利用して補因子行列を構築し、目標とする性能を達成する制御器を得ることができる。
３．逆システムの構築：二重既約分解では、伝達関数\(G(s)\)の逆関数や補因子を明示的に構築できる。これにより、逆システムをモデル化しやすくなり、逆制御問題の解決に役立つ。
４．デカップリングと独立制御：多入力多出力（MIMO）システムでは、各入力と出力を独立に制御するためのデカップリング（一入力一出力（SISO）システムへの分離）が求められる。二重既約分解は、MIMOシステムをデカップリングして独立制御するための有効な手法となる。