10. 電磁誘導
電磁誘導とは、磁場の変化によって導体内に電流(誘導電流)が発生する現象で、 ファラデーの法則 によって説明される。電磁誘導は、磁場の変化によって起こる ことが特徴で、以下のような状況で発生する。
・コイルの中を通る磁束の変化:磁石をコイルに近づけたり遠ざけたりすると、コイル内の磁場が変化し、電流が発生する。磁場が一定のままだと電流は発生しない。
・導体が磁場内を動く(フレミングの右手の法則):導体を磁場内で動かすと、電子が移動して電位差(起電力)が発生し、電流が流れる。
ファラデーの法則
図1のように、コイルを鎖交する(貫く)磁束の増減に時間変化を与えると、コイルに磁束の変化に応じた起電力\(e\)が発生する。このときコイルが閉じた回路であれば、コイルにはこの起電力により電流が流れる。この現象を電磁誘導現象という。電磁誘導により発生する起電力を誘導起電力、このときの電流を誘導電流という。
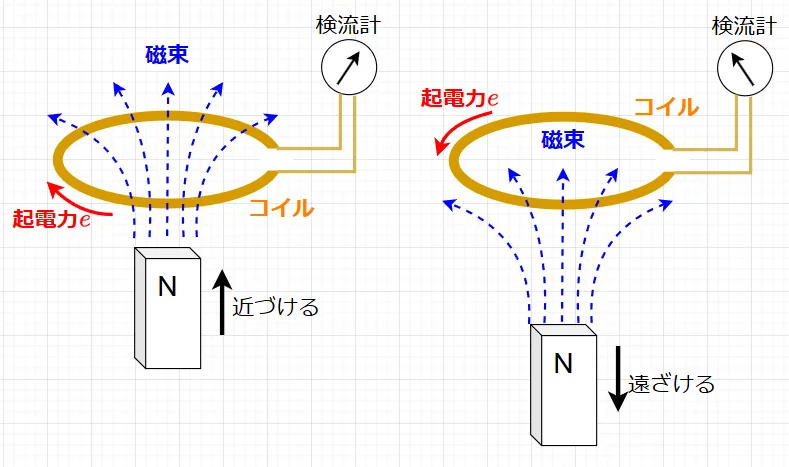
図1の左図は、磁石を近づけることで、コイルを貫く磁束が増加する。このとき、コイルには誘導起電力\(e\)が赤矢印の方向に発生する。この方向は、誘導電流により発生する磁束(右ネジの法則に従う方向)が、磁石による磁束の増加を妨げる方向(磁束を減少させる方向)である。一方、図1の右図は、磁石を遠ざけることで、コイルを貫く磁束が減少する。このとき、コイルには誘導起電力\(e\)が赤矢印の方向に発生する。この方向は、誘導電流により発生する磁束(右ネジの法則に従う方向)が、磁石による磁束の減少を妨げる方向(磁束を増加させる方向)である。
ファラデーの電磁誘導の法則は、「電磁誘導によって回路(コイル)に誘起される起電力は、その回路と鎖交する(貫く)磁束の時間変化の割合に比例する。」これを式で表すと、1巻のコイルと鎖交する磁束が\(\Delta t\)[s]間に\(\Delta \Phi\)[Wb]の割合で変化すると、誘導起電力\(e\)は、$$e= - \frac{\Delta \Phi}{\Delta t} \;[\text{V}]\\\text{微分形式では、} e= -\frac{d\phi}{dt}\;[\text{V}] \;\;\; \cdots (1)$$と書ける。式の(\(-\))符号は、誘導起電力の向きが磁束の変化を常に妨げようとする向きに発生すること(レンツの法則)を表している。
N巻コイルの誘導起電力
式(1)は、1巻のコイルに鎖交する磁束が、「1秒間に1 [Wb]の割合で変化すれば1 [V]の誘導起電力を発生する」ということを意味している。従って、コイルの巻き数が\(N\)回とすれば、1巻に生じる起電力の\(N\)倍の起電力が発生することになる。$$e = - N\frac{d \phi}{dt} \;[\text{V}]$$
磁界中で運動する導体の起電力
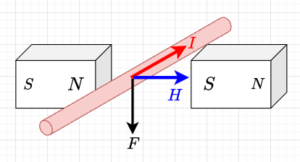
図2に示すように一様磁界(X印、画面の表から裏の方向)の中で導体が運動したときに回路に生ずる起電力を考える。図2(a)は、導体が速度\(v\)で下方に運動した場合で、導体と回路で構成される閉ループの面積が増加するので閉ループ内の磁束は増加することになる。従って、この磁束の増加を妨げる方向に、回路に流れる電流による磁束が発生するように起電力が生ずる。従って、起電力\(e\)は赤矢印の方向となる。
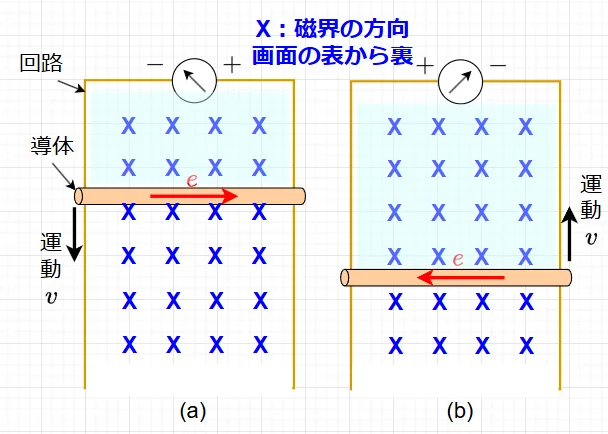
図2(b)は、導体が速度\(v\)で上方に運動した場合で、導体と回路で構成される閉ループの面積は減少するので閉ループ内の磁束は減少することになる。従って、この磁束の減少を妨げる方向に、回路に流れる電流による磁束が発生するように起電力が生ずる。従って、起電力\(e\)は赤矢印の方向(図2(a)と逆方向)となる。
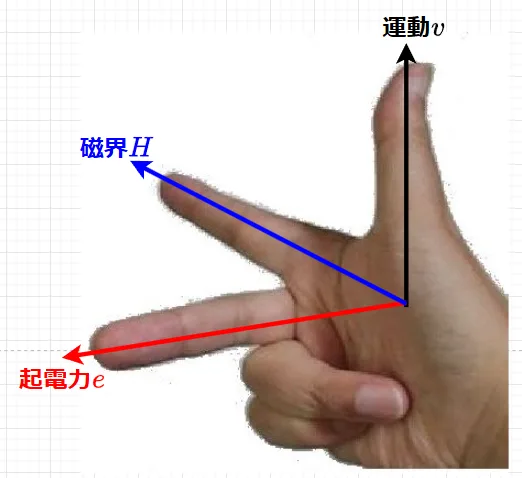
この磁界\(H\)、運動\(v\)、起電力\(e\)それぞれの方向の関係を右手の三指にあてはめて表したのが、図3に示すフレミングの右手の法則である。フレミングの右手の法則は、フレミングの左手の法則と対称の関係にあり、導体が磁界中で運動して磁束を切るときの、誘導起電力の方向を知るための法則である。
磁束密度が\(B\)[T]の平等磁界中で長さ\(l\)[m]の導体を、磁界と直角方向に\(v\)[m/s]の一定速度で直線運動するときの誘導起電力\(e\)の大きさを考える。
導体が\(\Delta t\)[s]間に進む距離は、\(v \Delta t\)[m]なので、\(\Delta t\)[s]間に導体によって切られる磁束数を\(\Delta \Phi\)[Wb]とすると、$$\Delta \Phi = vBl \Delta t \;[\text{Wb}]$$となる。誘導起電力\(e =\Delta\Phi / \Delta t\)なので、$$e = vBl \;[\text{V}]$$と表せる。
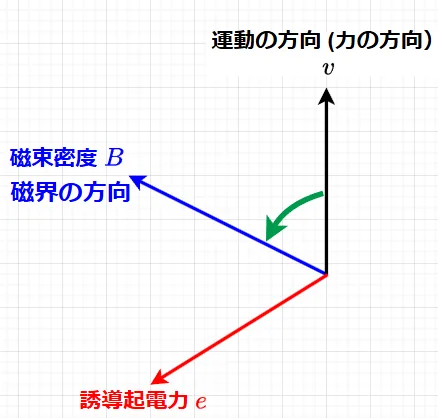
\(e,\;v,\;B\)は大きさと方向を持っているのでベクトルと考えると、起電力\(e\)はベクトル積(ベクトルの外積)で表せ、式(2)となる。$$e = (v \times B)l \;\;\;\cdots (2)$$
式(2)より、図4に示すように、磁界中の導体を動かしたときにに生じる誘導起電力\(e\)の方向は、導体の運動方向のベクトルを磁界の方向に回転させた(図4の緑の矢印の方向へ回転)時の右ネジの進む方向(右ネジの法則)となる。これを3本の指で表したのがフレミングの右手の法則なので、右ネジの法則が理解できていれば、3本の指の向きで手首が捻じれてしまうフレミングの右手の法則は無用である。また、力(運動の方向)から磁(磁界)の方向に右手の4本の指を折り曲げたときの親指の方向が電(誘導起電力の方向)となるので、力→磁→電(力磁電:電磁力の逆)で記憶すれば、右手のどの指が運動の方向なのか、磁界なのか悩む必要もない。