14. サーボ型一般化分散制御

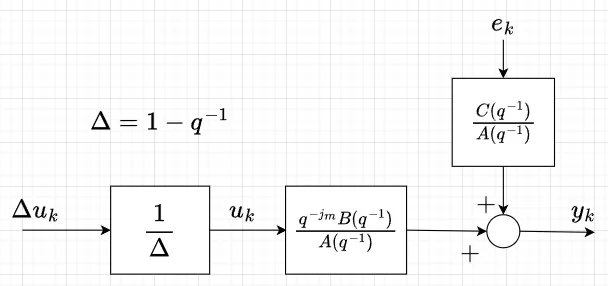
閉ループ制御系で外部入力として目標値、外乱があり、それらの変化によって定常偏差が生じるときは、内部モデル原理に基づいて制御系の構造を見直す必要がある。外部入力がステップ状に変化する場合には、そのモデルとして\(\frac{1}{1-q^{-1}}\)（積分器）を前置補償器として設ける。図１に制御対象の前に補償器\(\frac{1}{\Delta}\)を設置した構成を示す。\(\Delta = 1-q^{-1}\)である。

よって、$$\Delta A(q^{-1})y_k = q^{-j_m}B(q^{-1}) \Delta u_k + \Delta C(q^{-1})e_k \;\;\; \cdots (2) \\ A(q^{-1}) = 1 + a_1 q^{-1} + a_2 q^{-2} + \cdots +a_n q^{-n} \\ B(q^{-1}) = b_0 + b_1 q^{-1} + b_2 q^{-2} + \cdots + b_m q^{-m} \\ C(q^{-1}) = 1 + c_1 q^{-1} + c_2 q^{-2} + \cdots c_l q^{-l}$$である。
一般化出力は、$$\phi_{k + j_m} = P(q^{-1})y_{k+j_m} + S(q^{-1}) \Delta u_k - R(q^{-1}) w_{k+j_m} \;\;\; \cdots (3)$$で定義する。また、$$P(q^{-1}) C(q^{-1}) = \Delta A(q^{-1}) F(q^{-1}) + q^{-j_m} G(q^{-1}) \;\;\; \cdots (4)$$とする。ここで、$$F(q^{-1}) = 1 + f_1 q^{-1} + f_2 q^{-2} + \cdots + f_{j_m -1}q^{-(j_m-1)} \\ G(q^{-1}) = g_0 + g_1 q^{-1} + g_2 q^{-2} + \cdots + g_{n_3} q^{-n_3} , \quad n_3 = \text{max} \left\{n, n_p +1-j_m \right\}$$である。

14-1. 評価関数\(J_3 = E[\phi_{k+j_m} ^2]\)を最小にする制御則

式(2)の両辺に\(q^{j_m}F(q^{-1})\)を掛ける。$$\Delta A(q^{-1})F(q^{-1})y_{k+j_m} = B(q^{-1})F(q^{-1}) \Delta u_k + \Delta C(q^{-1})F(q^{-1})e_{k+j_m}$$この式の左辺\(Delta A(q^{-1})F(q^{-1})\)に式(4)を代入すると、$$P(q^{-1})C(q^{-1})y_{k+j_m} = G(q^{-1})y_k + B(q^{-1})F(q^{-1}) \Delta u_k + \Delta C(q^{-1})F(q^{-1})e_{k+j_m}$$となる。よって、$$P(q^{-1})y_{k+j_m} = \frac{1}{C(q^{-1})} \left\{G(q^{-1})y_k + B(q^{-1})F(q^{-1}) \Delta u_k \right\} + \Delta F(q^{-1})e_{k+j_m}$$である。これを式(3)に代入すると、$$\phi_{k+j_m} = \frac{1}{C(q^{-1}) }\left[G(q^{-1})y_k + \left\{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})\right\}\Delta u_k \\ - C(q^{-1})R(q^{-1})w_{k+j_m}\right] + \Delta F(q^{-1})e_{k+j_m} \;\;\; \cdots (5)$$ となる。この式を評価関数\(J_3\)に代入する。式(5)の第1項と第2項において、\(y_k\)と\(e_k\)には相関があるが、それ以外は無相関であるので、評価関数\(J_3\)をほぼ最小にするために、式(5)の\([\quad]\)内を0にすること考える。従って、操作量は、$$u_k = \frac{1}{\Delta} \frac{C(q^{-1})R(q^{-1})w_{k+j_m} - G(q^{-1})y_k}{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})} \;\;\; \cdots(6)$$となる。\(y_k\)と\(e_k\)の間には相関があるので、式(6)の操作量は準最適制御となる。
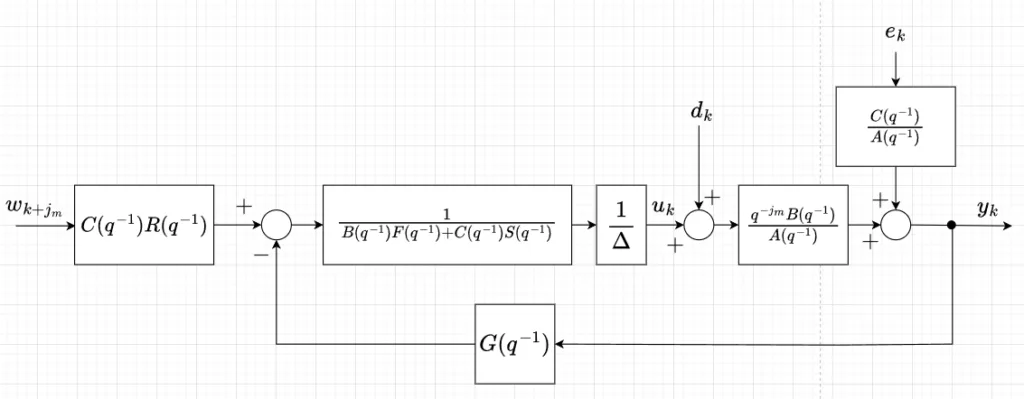
図２にサーボ型一般化最小分散制御系のブロック線図を示す。

14-2. サーボ型一般化最小分散制御系の特性(1)

サーボ型一般化最小分散制御系（図２）において、外部入力\(w_k,\;e_k\)から出力\(y_k\)までの特性を求めよ。

解答例：式(6)の操作量\(u_k\)を制御対象\(A(q^{-1})y_k = q^{-j_m}B(q^{-1})u_k + C(q^{-1})e_k\)に代入すると、$$\Delta A(q^{-1})\left\{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})\right\}y_k \\ =q^{-j_m} B(q^{-1})\left\{C(q^{-1})R(q^{-1})w_{k+j_m} - G(q^{-1})y_k\right\} + \Delta C(q^{-1})\left\{B(q^{-1})F(q^{-1}) \\ + C(q^{-1})S(q^{-1})\right\}e_k$$となる。この式を整理すると、$$\left\{B(q^{-1})\left(\Delta A(q^{-1})F(q^{-1}) + q^{-j_m}G(q^{-1})\right) + \Delta A(q^{-1})C(q^{-1})S(q^{-1})\right\}y_k \\= B(q^{-1})C(q^{-1})R(q^{-1})w_k + \Delta C(q^{-1})\left\{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})\right\}e_k$$となる。左辺に式(4)を代入すると、$$\left\{B(q^{-1})P(q^{-1})C(q^{-1}) + \Delta A(q^{-1})C(q^{-1})S(q^{-1})\right\}y_k \\= B(q^{-1})C(q^{-1})R(q^{-1})w_k + \Delta C(q^{-1})\left\{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})\right\}e_k$$なので、両辺を\(C(q^{-1})\)で割り、$$\left\{B(q^{-1})P(q^{-1})+ \Delta A(q^{-1})S(q^{-1})\right\}y_k \\= B(q^{-1})R(q^{-1})w_k + \Delta \left\{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})\right\}e_k$$となる。$$T^{'}(q^{-1}) = B(q^{-1})P(q^{-1})+ \Delta A(q^{-1})S(q^{-1})$$とおく。これは、閉ループ制御系の特性多項式である。この\(T^{'}(q^{-1})\)を使うと、$$y_k = \frac{B(q^{-1})R(q^{-1})}{T^{'}(q^{-1})}w_k + \frac{\Delta \left\{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})\right\}}{T^{'}(q^{-1})}e_k \;\;\; \cdots (7)$$となる。

14-3. サーボ型一般化最小分散制御系の特性(2)

サーボ型一般化最小分散制御系（図２）において、外部入力\(w_k,\;e_k\)から操作量\(u_k\)までの特性を求めよ。

解答例：式(6)の\(u_k\)に制御対象\(A(q^{-1})y_k = q^{-j_m} B(q^{-1})u_k + C(q^{-1})e_k\)の\(y_k\)を代入し、\(y_k\)を消去すると、$$\Delta A(q^{-1})\left\{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})\right\}u_k \\ = A(q^{-1})C(q^{-1})R(q^{-1})w_{k+j_m} - G(q^{-1})\left\{q^{-j_m} B(q^{-1})u_k +C(q^{-1})e_k\right\} \\ \quad \\ \left\{\Delta A(q^{-1})B(q^{-1})F(q^{-1}) + q^{-j_m} G(q^{-1})B(q^{-1}) + \Delta A(q^{-1})C(q^{-1})S(q^{-1}) \right\}u_k \\=A(q^{-1})C(q^{-1})R(q^{-1})w_{k+j_m} - G(q^{-1})C(q^{-1})e_k$$となる。この左辺に式(4)の\(P(q^{-1}) C(q^{-1}) = \Delta A(q^{-1}) F(q^{-1}) + q^{-j_m} G(q^{-1})\)を代入すると、$$C(q^{-1})\left\{B(q^{-1})P(q^{-1}) + \Delta A(q^{-1})S(q^{-1})\right\}u_k \\= C(q^{-1})\left\{A(q^{-1})R(q^{-1})w_{k+j_m} - G(q^{-1})\right\}e_k$$となる。両辺を\(C(q^{-1})\)で割って、\(T^{'}(q^{-1}) = B(q^{-1})P(q^{-1})+ \Delta A(q^{-1})S(q^{-1})\)を使うと、$$u_k = \frac{A(q^{-1})R(q^{-1})}{T^{'}(q^{-1})}w_{k+j_m} - \frac{G(q^{-1})}{T^{'}(q^{-1})}e_k \;\;\; \cdots (8)$$となる。

14-4. 水位制御モデルのサーボ型一般化最小分散制御

12. 最小分散制御(2)で示した数位制御モデルにサーボ型一般化最小分散制御を適用せよ。

解答例：式(9)で示すむだ時間を有する水位制御モデルをサンプリング周期\(T=3 \text{[s]}\)で離散化する。$$G(s) = \frac{30}{25.04 s^3 + 78.84 s^2 + 41.1 s +1}e^{-9s} \;\;\; \cdots (9)$$
離散化結果は、以下となる。$$A(q^{-1})y_k = q^{-3}B(q^{-1})u_k \\ A(q^{-1})=1−1.080q^{-1}+0.1426q^{-2}−7.855×10^{-5} q^{-3} \\ B(q^{-1})=0.9925+0.8683q^{-1}+0.01413q^{-2}$$重み多項式を$$P(q^{-1}) = 1,\quad S(q^{-1})=500, \quad R(q^{-1})=1$$とする。$$(P(q^{-1}) C(q^{-1}) = \Delta A(q^{-1}) F(q^{-1}) + q^{-j_m} G(q^{-1})$$より、$$1 = (1-q^{-1})(1−1.080q^{-1}+0.1426q^{-2}−7.855×10^{-5} q^{-3}) \\ \times (1+f_1 q^{-1} +f_2 q^{-2}) + q^{-3}(g_0 + g_1 q^{-1} + g_2 q^{-2} + g_3 q^{-3})$$となり、この式の右辺を展開し、係数を比較することで、$$F(q^{-1}) = 1 + 2.080q^{-1} + 3.104q^{-2} \\ G(q^{-1}) = 4.056 - 3.498q^{-1} + 0.4428q^{-2} + 2.438 \times 10^{-4} q^{-3}$$が求まる。

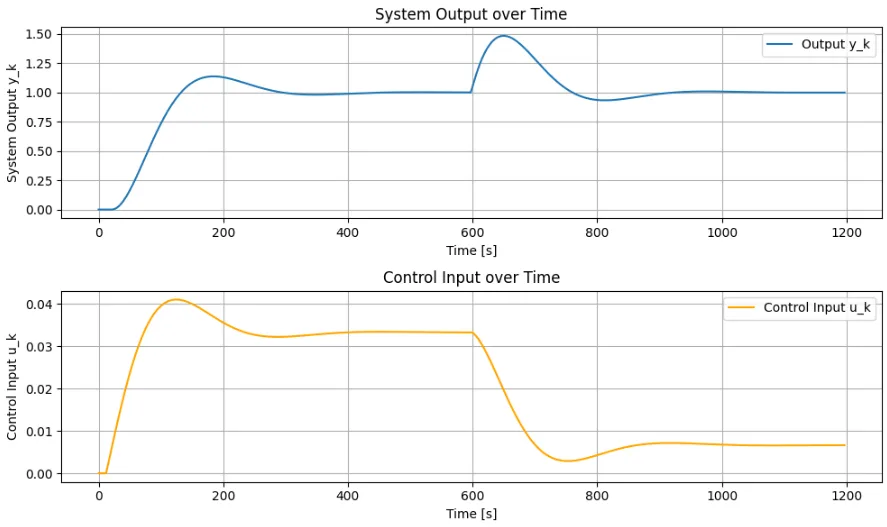
※Pythonによる時間応答シミュレーションのスクリプト例を示す。この例では、目標値\(w_k\)を単位ステップとして、さらに600[s]後に制御対象の入力側にステップ状の外乱\(d_k\)（大きさ0.05)を加えている。このサーボ型一般化最小分散制御系では、目標値への応答では定常偏差が無く、制御対象の入力側にステップ状の外乱が入っても抑制できることが分かる。図３にシミュレーション結果を示す。

import numpy as np
import matplotlib.pyplot as plt
# Simulation parameters
T = 3                   # Sampling period [s]
N = 400                 # Number of steps (total time = 1200s)
j_m = 3                 # Prediction step
t = np.arange(N) * T    # Time vector
# Initialize signals
y = np.zeros(N)         # System output
u = np.zeros(N)         # Control input
w = np.ones(N)          # Reference input (step)
d = np.zeros(N)         # Disturbance
# Add step disturbance to u_k at t = 600s (k = 200)
d[200:] = 0.05          # Disturbance of magnitude 0.05
# Define polynomials
B = np.array([0.9925, 0.8683, 0.01413])
F = np.array([1.0, 2.080, 3.104])
G = np.array([4.056, -3.498, 0.4428, 0.0002438])
A = np.array([1.0, -1.080, 0.1426, -7.855e-5])
S = 500.0
Delta = np.array([1.0, -1.0])  # 1 - q^-1
# Precompute B*F + S
BF = np.convolve(B, F)
BF_S = BF.copy()
BF_S[0] += S
# Simulation loop
for k in range(5, N):
    # y vector for G(q^-1)
    y_vec = y[k-1:k-5:-1] if k >= 4 else np.zeros(4)
    Gy = np.dot(G[:len(y_vec)], y_vec)
    # Future reference
    if k + j_m < N:
        wk_jm = w[k + j_m]
    else:
        wk_jm = w[-1]
    # Numerator and approximate denominator
    num = wk_jm - Gy
    denom_approx = BF_S[0]  # use only first coefficient
    u_pre = num / denom_approx
    # Apply Delta inverse
    u[k] = u[k-1] + u_pre
    # Compute Bu (q^-3 B(q^-1) u_k)
    Bu = 0.0
    if k >= 5:
        Bu = B[0]*u[k-3] + B[1]*u[k-4] + B[2]*u[k-5] + d[k] #外乱の印可
    # Compute y[k] using A(q^-1)
    y[k] = (-A[1]*y[k-1] - A[2]*y[k-2] - A[3]*y[k-3]) + Bu
# Plot results
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(t, y, label="Output y_k")
plt.xlabel("Time [s]")
plt.ylabel("System Output y_k")
plt.title("System Output over Time")
plt.grid(True)
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(t, u, label="Control Input u_k", color='orange')
plt.xlabel("Time [s]")
plt.ylabel("Control Input u_k")
plt.title("Control Input over Time")
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

14-5. 目標値に対する定常偏差

サーボ型一般化最小分散制御系において、目標値を単位ステップ状に変化させたときに生じる定常偏差を求めよ。

解答例：時刻\(k\)における制御偏差\(err_k\)を目標値\(w_k\)と出力\(y_k\)との差で定義する。\(err_k = w_k - y_k\)である。ここで、出力\(y_k\)は式(7)より、$$y_k = \frac{B(q^{-1})R(q^{-1})}{T^{'}(q^{-1})}w_k + \frac{\Delta \left\{B(q^{-1})F(q^{-1}) + C(q^{-1})S(q^{-1})\right\}}{T^{'}(q^{-1})}e_k $$ここで、$$T^{'}(q^{-1}) = B(q^{-1})P(q^{-1}) + \Delta A(q^{-1})S(q^{-1})$$である。（\(\Delta = 1 - q^{-1}\)）
\(e_k\)は平均値ゼロの白色雑音であるので、制御偏差\(err_k\)の期待値は、$$E[err_k] = \frac{T^{'}(q^{-1}) - B(q^{-1})R(q^{-1})}{T^{'}(q^{-1})} w_k$$となる。目標値\(w_k\)が単位ステップのときの定常偏差の期待値\(E[err_\infty]\)は、最終値定理を使って以下となる。$$E[err_\infty] = \lim_{k \to \infty} E[err_k] = \lim_{q \to 1} (1-q^{-1})\frac{T^{'}(q^{-1}) - B(q^{-1})R(q^{-1})}{T^{'}(q^{-1})} \cdot \frac{q}{q-1} \\ = \lim_{q \to 1} \frac{B(q^{-1})P(q^{-1}) + \Delta A(q^{-1})S(q^{-1}) - B(q^{-1})R(q^{-1})}{T^{'}(q^{-1})} \\ = \frac{B(1)\left\{P(1) - R(1) \right\}}{T^{'}(1)}$$　これより、重み多項式を\(P(1) = R(1)\)に定めれば、目標値のステップ状変化に対して定常偏差なく追従することが保証される。