39. モータのモデル化(1)
電気ー機械系の典型である電気モータの数学モデルに関して説明する。
(モータのモデル化に関連した)電気―機械系のまとめ
モータのモデル化に関連した電気、機械系の動的システムについて、まとめて紹介する。
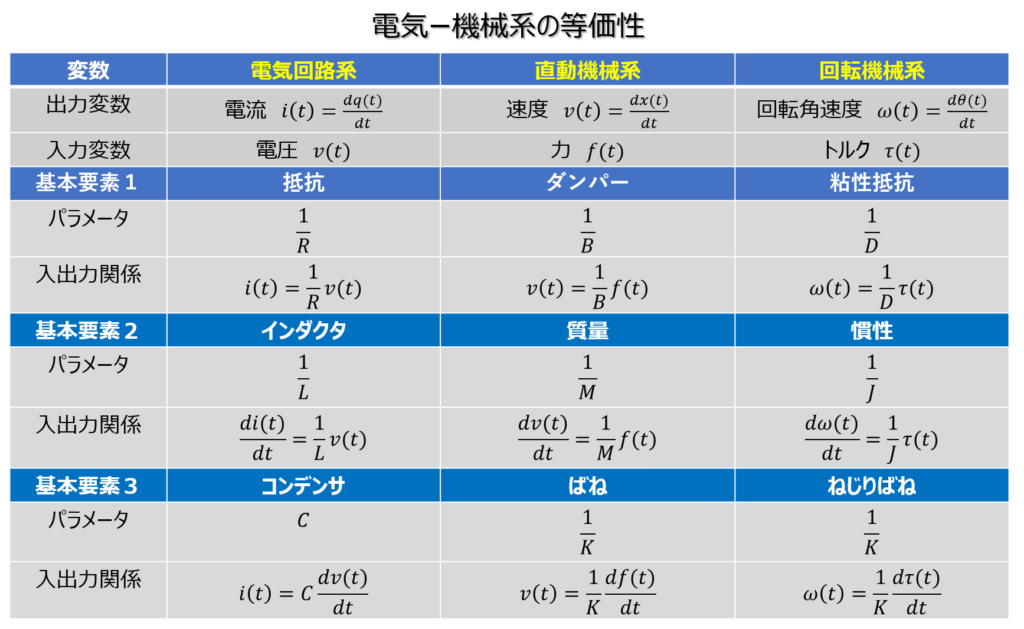
電気系の動的システム

直動系の動的システム

回転機械系の動的システム
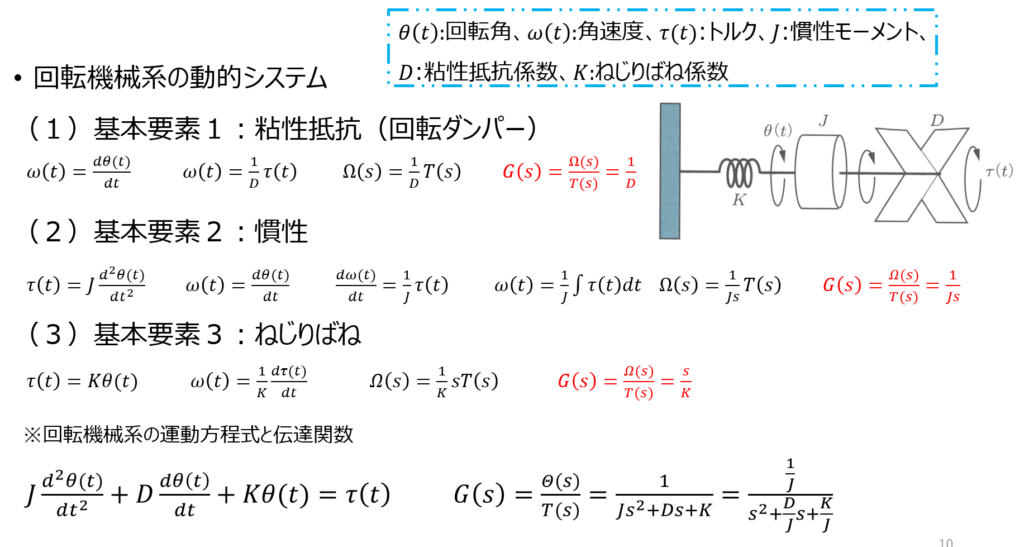
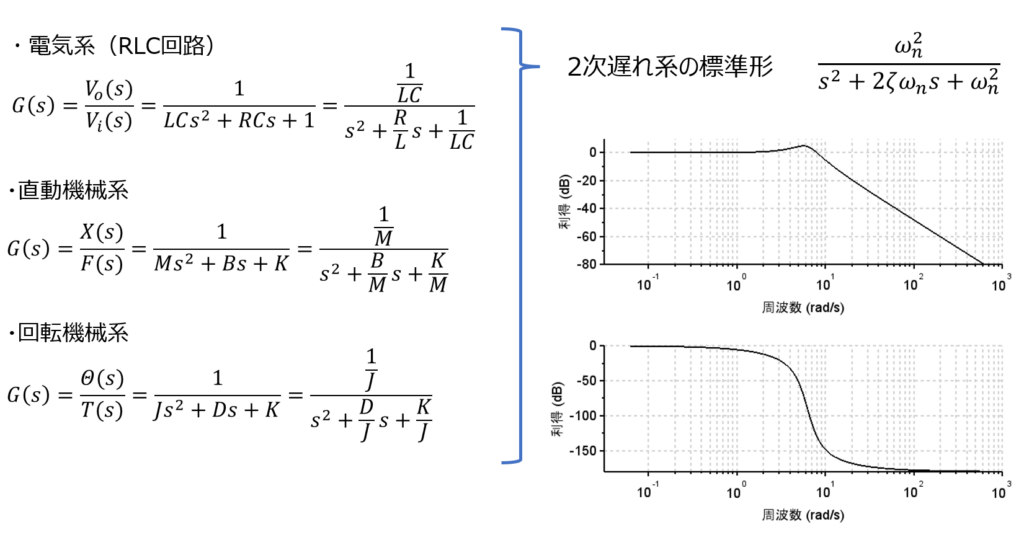
数式モデル等価性
\(V_i(s), V_o(s)\)は、RLC回路への入力電圧と出力電圧。\(F(s),X(s)\)は、直動機械系への力と変位。\(T(s),\theta(s)\)は、回転機械系へのトルクと角度。
各動的システムを数式モデルと表すと似たような形式となる。従って、1次遅れ系や2次遅れ系の標準形とその応答特性(ステップ応答やボード線図など)をイメージとして修得しておくと、様々な場面で役に立つ。
(余談)数式モデルの等価性は、基本的な物理現象を微分や積分で表現することに依っている(人間の物理現象の捉え方の問題?)。
慣性モーメント(イナーシャ)、トルク
・慣性回転体のモーメント \(J \left[kg\cdot m^2\right]\)
慣性モーメント\(J\)の基本は、回転体の中心を回る「回転体の質量\(M \left[kg\right]\)と回転体の半径\(R\left[m\right]\)の2乗との積」である。$$J=M\times R^2$$
・回転トルク \(\tau \left[N\cdot m\right]\)
イナーシャ\(J\) の回転体に角加速度\(\alpha=\frac{d^2\theta(t)}{dt^2} \left[rad/s^2\right]\) を生じさせるにはトルク\(\tau \left[N\cdot m\right]\)が必要となる。$$\tau = J \times \alpha$$
※力 \(F=m\times a\) \(m\):質量\(\left[kg\right]\) \(a\):加速度\(\left[ m/s^2\right]\)

