41. VCMの制御

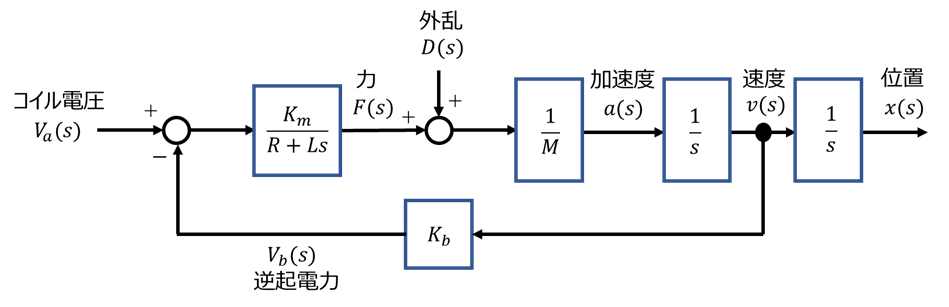
\(R\)：コイル抵抗［Ω］
\(L\)：コイルインダクタンス［H］
\(M\)：コイル質量［kg］
\(K_m\)：力定数［N/A］
\(K_b\)：逆起電力定数［V/(m/s)］
\(K_m = K_b\)

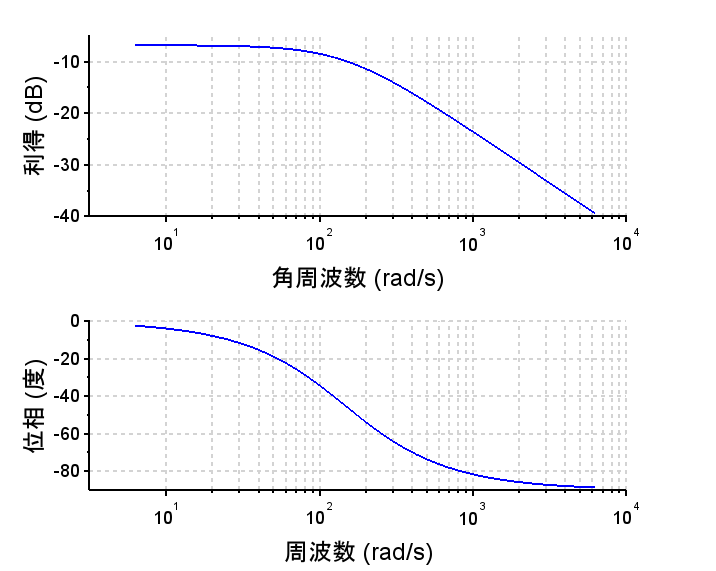
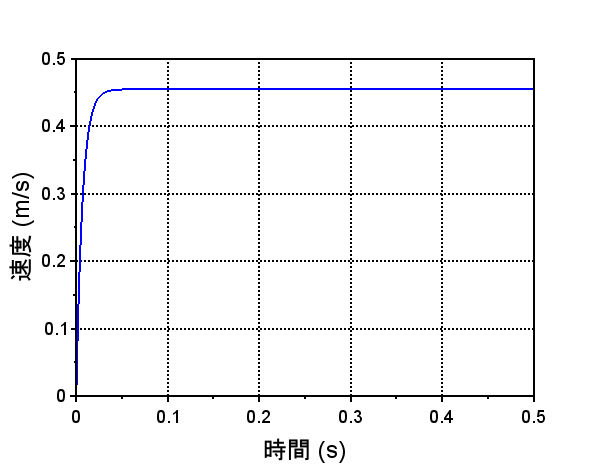
コイル電圧ー速度　伝達関数 \(P1(s)\)より、周波数応答特性、時間応答特性を求める。
•伝達関数、周波数特性より、一次遅れ系となっている。　［時定数：\(\tau=\frac{RM}{K_b K_m } \)］
•ステップ応答より一定電圧を印可することで一定速度になる。
•立ち上がり時間（時定数）は逆起電力によって影響を受ける。
•周波数特性より角周波数200[rad/s]以上で\(\frac{1}{s}\)（-20db/dec)特性になる。
•回転系ではないためタコメータ等による速度検出は難しいため、速度フィードバックは困難。（ポジションセンサー等を利用して信号処理をすることにより実装できるがコストがかかる。）

注：ステップ応答で一定速度になっているが、実際のVCMでは機械的なストッパなどで移動範囲が制限されているので、当然のことながら、一定速度が続くわけではない。

VCMの速度制御系の設計　(注：速度が検出できたと仮定して設計している）

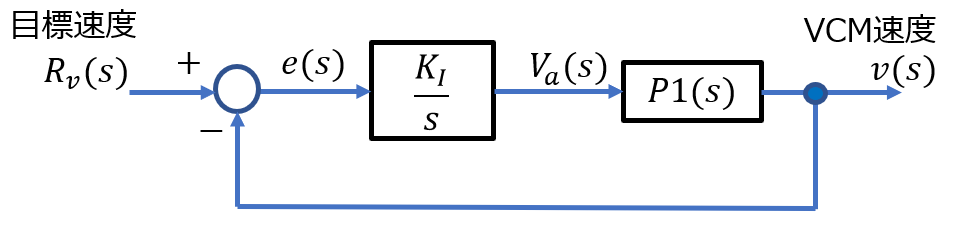
＊積分補償（積分制御器）の場合
ここでは、VCM速度が目標速度と一致するように、すなわち定常偏差\(e(s)=R_v(s) - v(s)\)が\(0\)になるように積分補償を使う場合を考える。勿論、ゲイン補償だけの制御器でゲインを大きくすることで、制御帯域を高くとることで定常偏差を低減することができるが、制御帯域を高くすると耐雑音性などの条件は厳しくなる。$$C(s)=\frac{K_I}{s} \enspace \enspace K_I=700$$ ゲイン交差周波数を200 [rad/s]となるように、\(K_I\)を調整した。

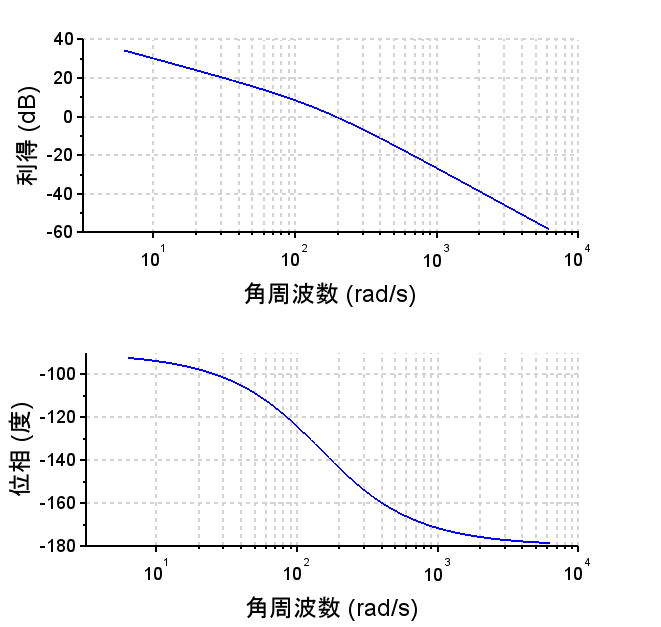
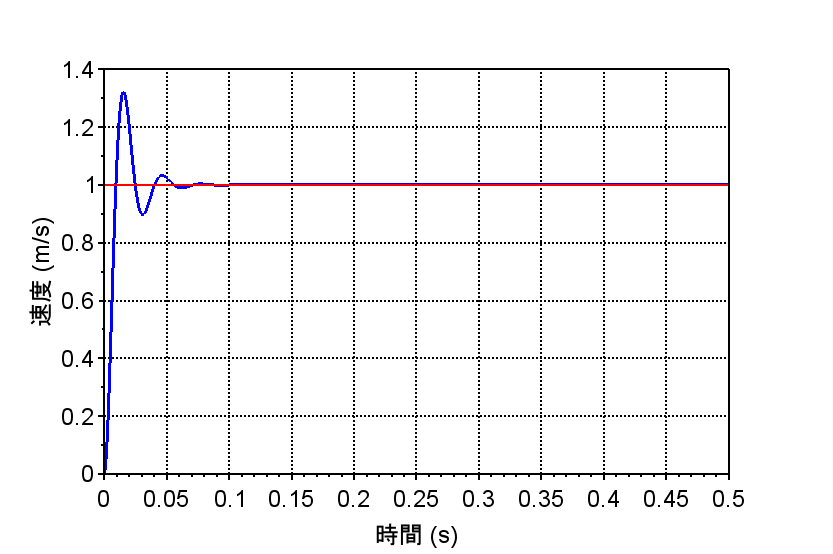
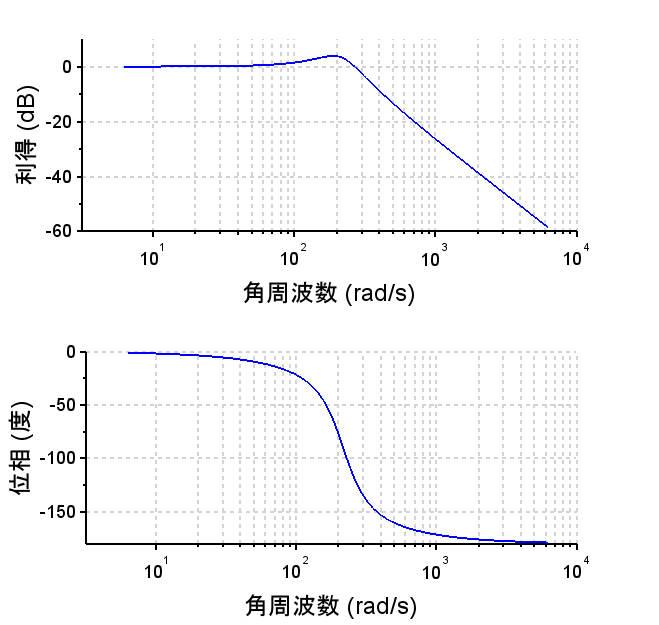
開ループ周波数応答特性から、ゲイン交差周波数200 [rad/s]で、位相余裕\(35\text{°}\)程度となっている。閉ループ周波数応答特性から、やや\(M_p\)値が大きく、行き過ぎ量が大きい傾向にある。また、ステップ応答特性より目標速度（赤線）との偏差が０にできている。オーバーシュートを低減するには帯域（ゲイン交差周波数）を下げる、積分補償の範囲を狭くする、位相進み補償器を追加する、などの方法が考えられる。これらの施策は、必要な制御仕様に応じて選択すれば良い。

VCMの特性（コイル電圧ー位置特性）

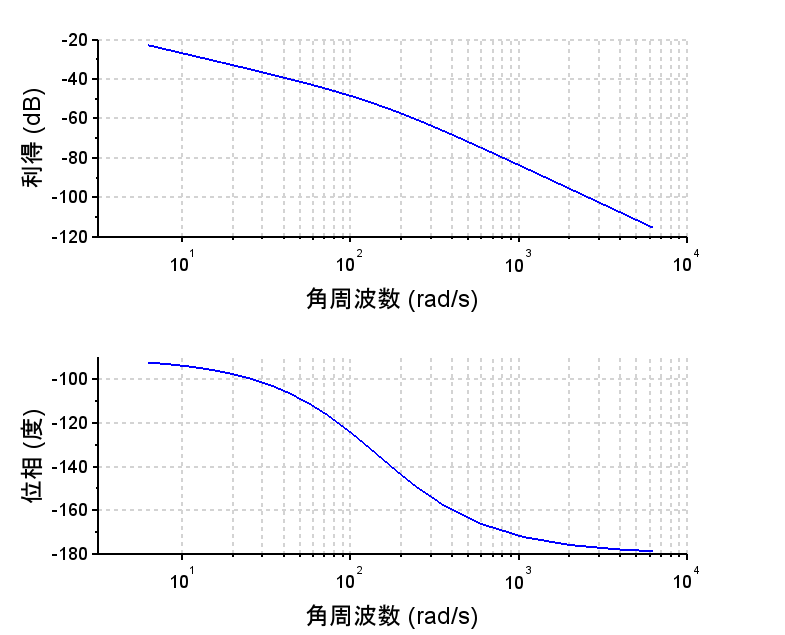
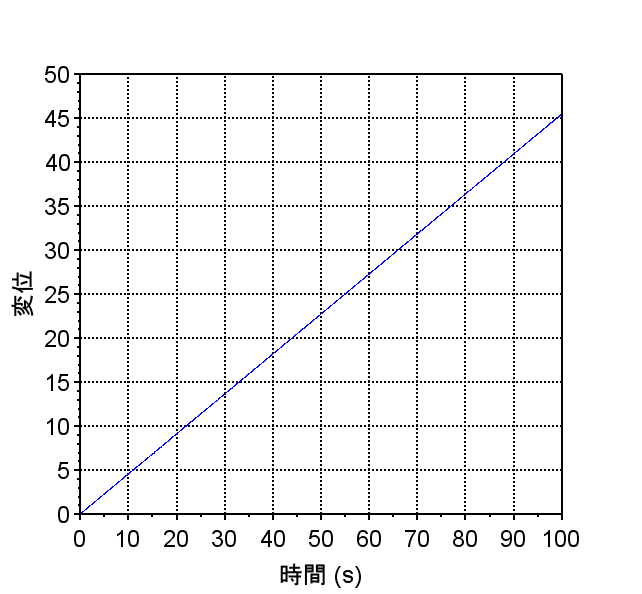
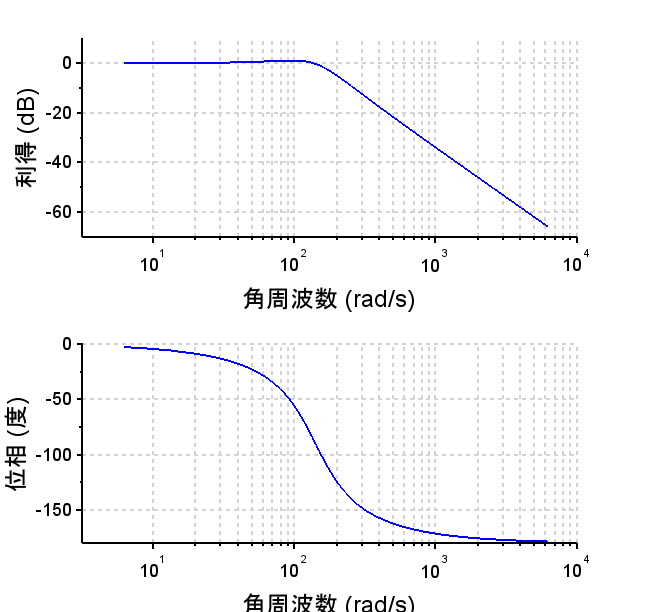
コイル電圧ー位置　伝達関数 \(P2(s)\)より、周波数応答特性、時間応答特性を求める。
•伝達関数、周波数特性より、二次系となっている。
•周波数特性より角周波数200[rad/s]以上で\(\frac{1}{s^2}\)（-40db/dec)特性になる。
•ステップ応答より一定電圧を印可することで位置が発散する。（不安定：安定限界）
•VCMだけでは不安定な系であるため、フィードバックによるゲイン補償や微分補償（位相進み補償）が必要である。
•\(P2(s)\)  は１型であるため、本質的にはゲイン補償で位置偏差を０にできる。

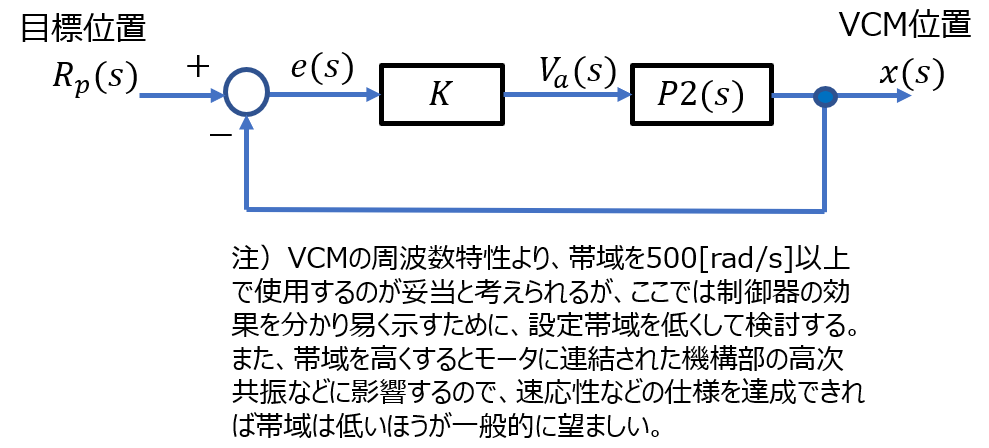
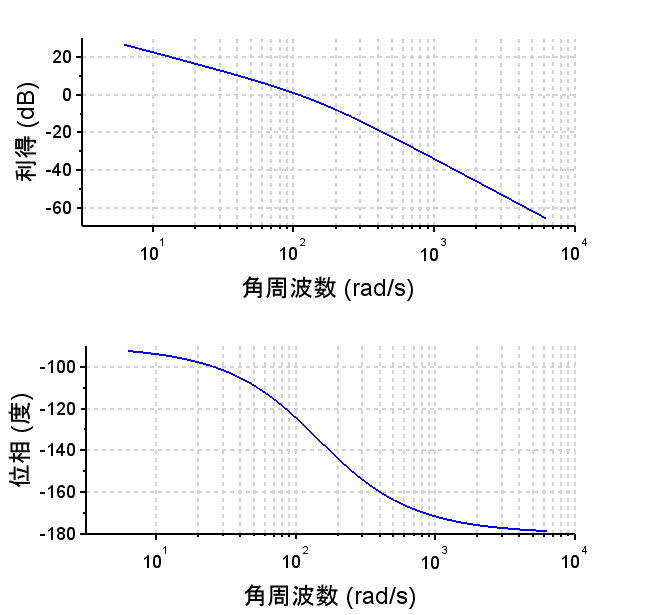
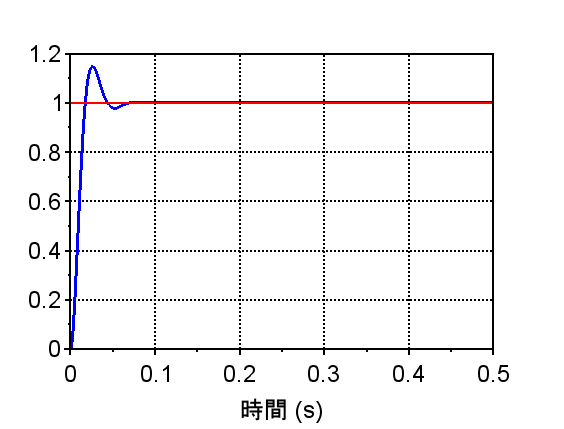
ゲイン補償の場合

\(C(s)=K\)（ゲイン補償）

ゲイン交差周波数を100[rad/s]にすることを考える。
VCMの周波数特性より、ゲインK=300（約 +50dB）とする。

・開ループ特性より、ゲイン交差周波数100[rad/s]で位相余裕は約55°、低域は\(\frac{1}{s}\)特性であるため、ステップ応答での定常位置偏差は０になると推測できる。
・閉ループ特性より、\(M_p\)値は小さくステップ応答での行き過ぎ量は小さい と推測できる。
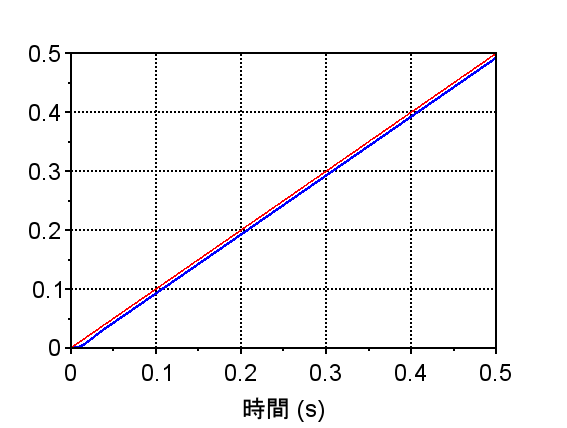
・ステップ応答より、定常位置偏差が０である。また、過渡特性は若干振動的となっている。（赤線：目標位置「ステップ信号」）
・ランプ応答より、定常速度偏差が生じる。（赤線：目標位置「ランプ信号」）
・この位置制御系では、目標位置に偏差０で静止させることができるが、目標位置が変化する場合、偏差が生じ十分に追従させることができない。

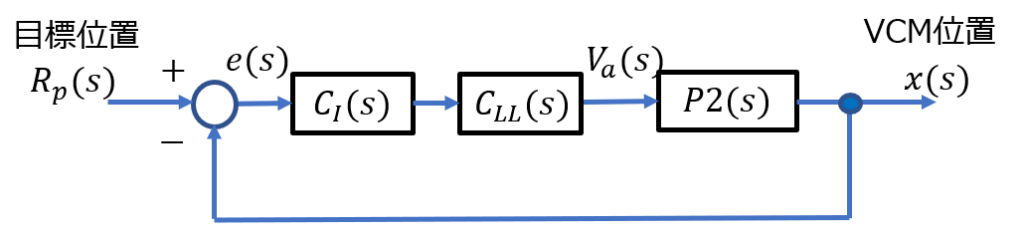
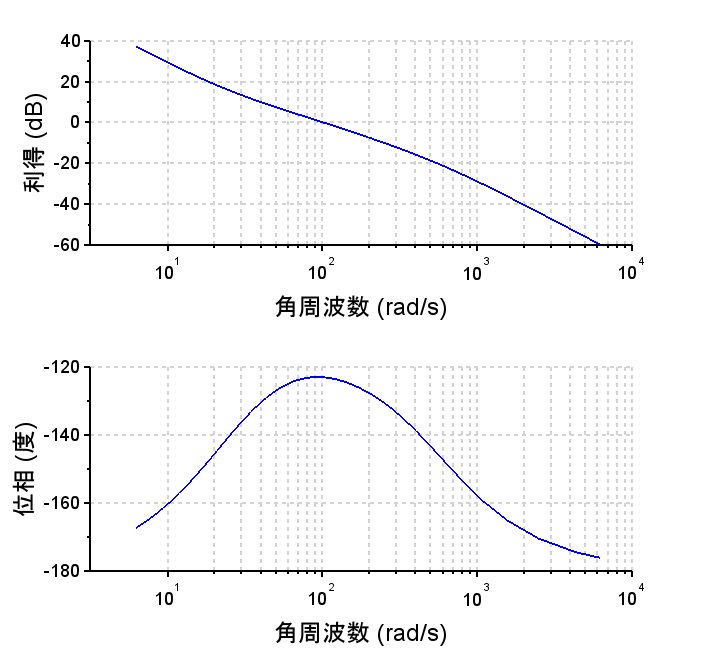
積分補償＋位相進み補償の場合

位相進み補償器：$$C_{LL} (s)=K \frac{1+saT}{1+sT}$$　積分補償器：$$C_I (s) = \frac{s+\frac{1}{T_I }}{s}$$ \(K=30\)、\( T=0.002\)、\( a=20\)、\(T_I=0.005\)
ゲイン交差周波数は100[rad/s]とする。

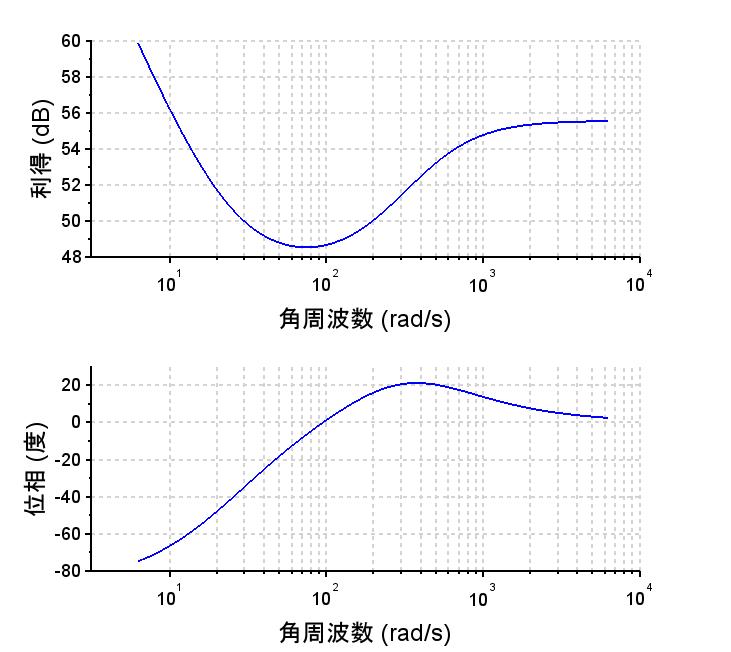
・位相進み＋積分補償器の周波数特性より、低域でのゲインは\(\frac{1}{s}\)特性（-20dB/dec）で上がっていることが分かる。これにより位相特性が劣化するが、位相進み補償器により、100から1000[rad/s]近傍における位相を改善している。これは、過渡応答での減衰特性の改善に寄与する。
・この構成では、局所フィードバック（速度検出）を必要としていない。位相進み補償器の微分特性により、速度を推定してフィードバックしていると考えることができる。（状態観測器の機能の一部を実現）

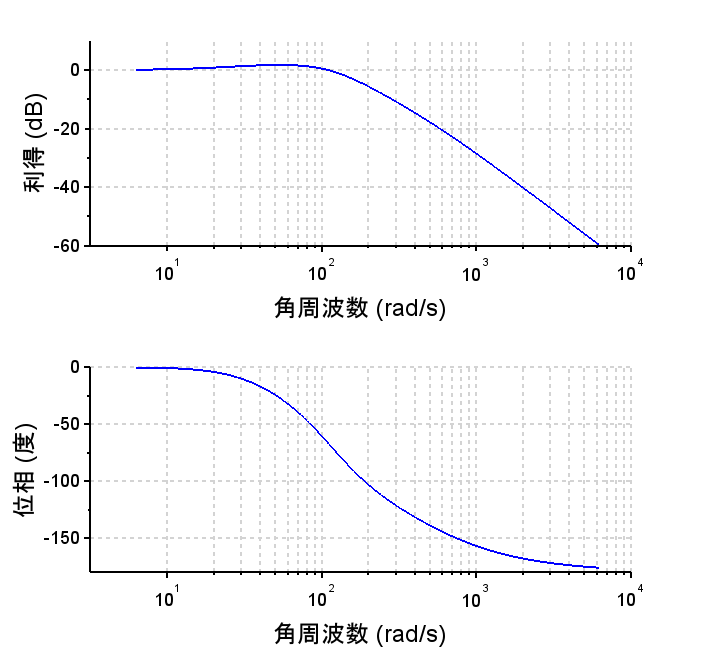
・開ループ特性より、ゲイン交差周波数100[rad/s]で位相余裕は約57°となっている。30[rad/s]以下の低域では\(\frac{1}{s^2}\)（-40dB/dec）特性となっているため、ステップ応答での定常位置偏差は０であり、ランプ応答での定常速度偏差も０になると推測できる。
・閉ループ特性より、M_p値は小さくステップ応答での行き過ぎ量は小さいと推測できる。また、位相特性もなだらかであるため、ステップ応答は非振動的と推測できる。

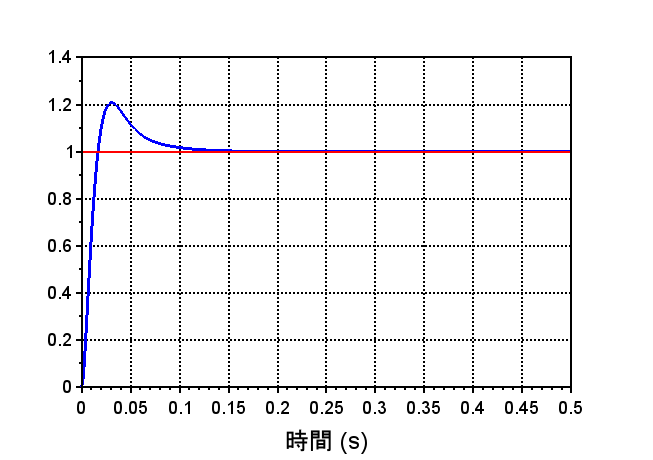
・ステップ応答より、定常位置偏差が０である。また、過渡特性は滑らかで非振動的となっている。
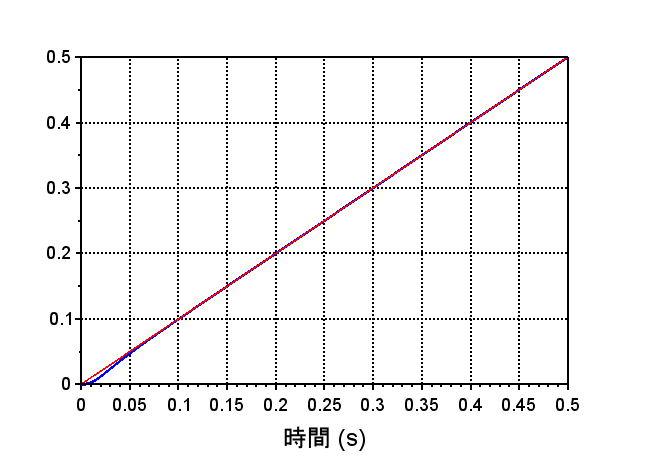
・ランプ応答より、定常速度偏差も０である。
・以上より、この位置制御系では、目標位置に偏差０で静止させることができる。また、目標位置が定速度で変化する場合でも追従できることがわかる。

※ステップ応答のオーバーシュートを低減するには、帯域を下げるなどの方法があるが、より良い制御を実現するには二自由度制御系にするのが望ましい。ただし、コストを勘案する必要がある。

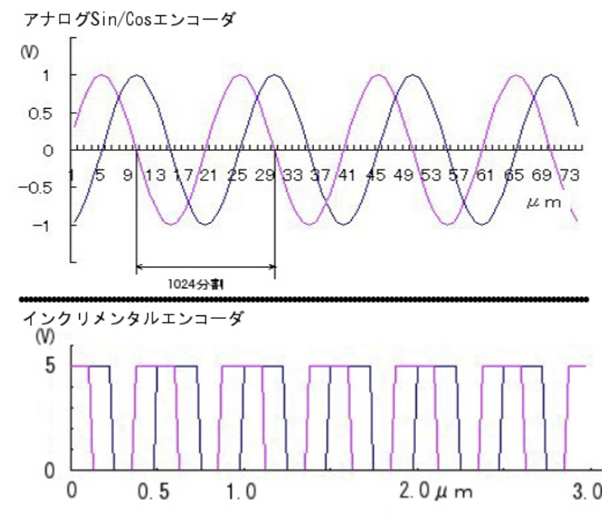
VCMの位置制御を行うために、VCMのキャリッジの位置を検出してフィードバックループを構成するために位置センサを取り付ける必要がある。

＊位置検出センサの例
・1Vpp 正弦波タイプリニアエンコーダ：光学式エンコーダ
・パルスタイプリニアエンコーダ：光学式エンコーダ
・干渉レーザ変位計：参照面と対象物からの反射光との干渉により、高精度な変位計測を行う

リニアエンコーダの詳細は、こちら（ミツトヨ　リニアエンコーダ）などを参照願いたい。