43. DCモータの制御(2)
サーボモータのタコメータフィードバック制御系の設計例
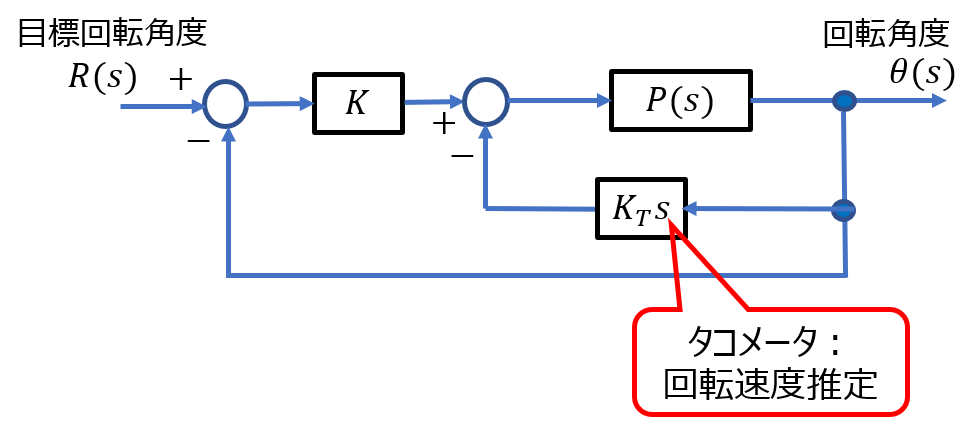
このような局所フィードバックによる制御手法は、古典制御理論の枠組みで多く使われてきたが、現代制御理論の状態フィードバックによって、MIMO(多入力多出力)系にも統一的に適用できるようになり、理論的に完成されたと言える。近年では、多様なセンサが開発され、局所フィードバックが比較的容易に実装できるようになった。
タコメータは最近では使用されることが少なくなったが、光学式エンコーダなどでも同様な設計法が使える。
【例】制御対象、制御仕様を以下として設計する。
制御対象: $$P(s)=\frac{10}{s(s+1)}$$
制御仕様:減衰率 \(\zeta=0.5\)
定常速度偏差 \(e_v=0.05\)
ブロック図より開ループ伝達関数\(L(s)\)は、$$L(s) = K\frac{P(s)}{1+K_T sP(s) }=K\frac{\frac{10}{s(s+1)}}{1+K_T s \frac{10}{s(s+1) }}$$ $$=\frac{10K}{s(s+1)+10K_T s} = \frac{10K}{s(s+10K_T+1)}$$となる。\(L(s)\)が1型のため定常位置偏差は0である。
閉ループ伝達関数\(T(s)\)は、$$T(s)=\frac{L(s)}{1+L(s)} =\frac{\frac{10K}{s(s+10K_T+1)}}{1+\frac{10K}{s(s+10K_T+1)}}$$ $$=\frac{10K}{s(s+10K_T+1)+10K} = \frac{10K}{s^2+(10K_T+1)s+10K}$$である。
標準2次系が、$$\frac{\omega_n^2}{s^2 + 2\zeta \omega_n s + \omega_n^2}$$なので、\(\omega_n = \sqrt{10K}\) 、\(2\zeta \omega_n =10K_T + 1\) 、制御仕様より\(\zeta=0.5\)とするので、 \(\sqrt{10K} = 10K_T + 1\)となる。
\(L(s)= \frac{10K}{s(s+10K_T+1)}\)で、制御仕様より、目標値は\(R(s)=\frac{1}{s^2}\)である。 速度偏差定数\(k_v\)は、$$k_v=\lim_{s \rightarrow 0}sL(s)=\frac{10K}{10K_T + 1}$$ 制御仕様より定常速度偏差 \(e_v=0.05\)なので、$$e_v = \frac{1}{k_v}=\frac{10K_T +1}{10K}\le 0.05$$ $$e_v=\frac{\sqrt{10K}}{10K}\le 0.05$$よって、\(K \ge 40\)となる。また、\(10K_T +1 \ge \sqrt{400} =20\) なので、\(K_T \ge 1.9\)である。
従って、設計値は\(K \ge 40\) 、 \(K_T \ge 1.9\)となる。
制御対象: \(P(s)=\frac{10}{s(s+1)}\)
制御仕様:減衰率 \(\zeta=0.5\)
定常速度偏差 \(e_v=0.05\)
\(K = 40\)、\(K_T =1.9\)の場合で計算する。
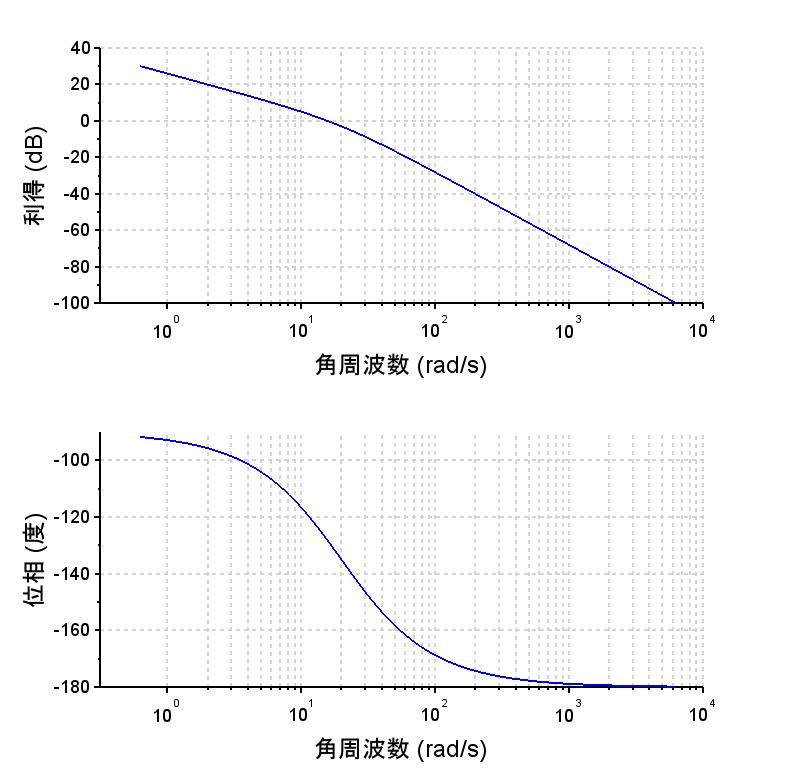
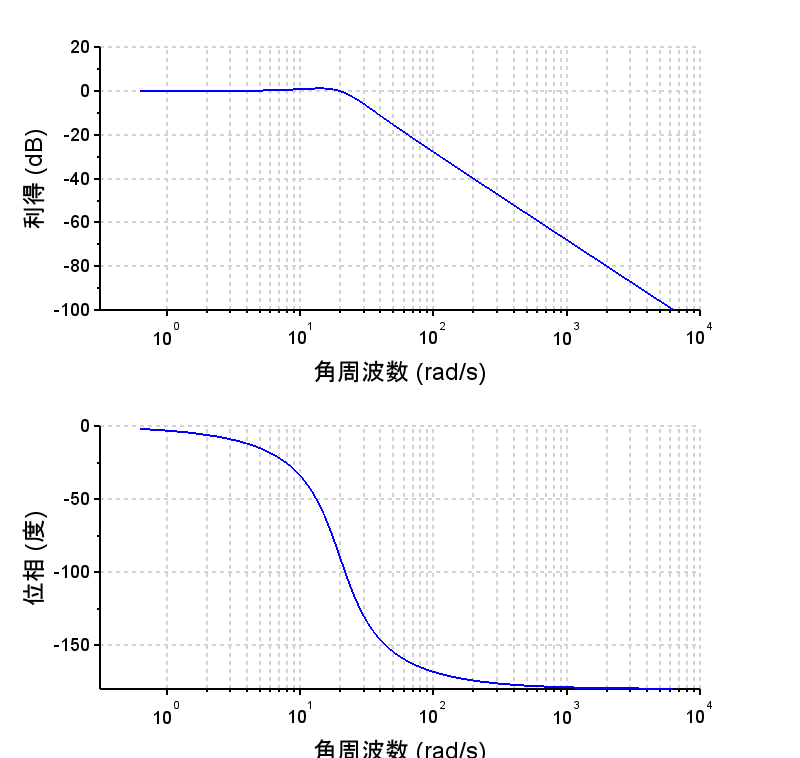
・開ループ周波数特性から位相余裕 約\(50\text{°}\)で、安定余裕は十分である。
・開ループ周波数特性から\(M_p\)値が大きくなく、制御帯域は凡そ250[rad/s]である。
・ステップ応答は、行き過ぎ量が大きくなく、定常位置偏差は0となっている。(1型系のため)
・ランプ応答から、定常速度偏差は0.05程度と制御仕様を満たしている。
・この設計値\(K = 40\)、\(K_T =1.9\)は、制御仕様を満たす条件の下限であるので、\(K , K_T\)を大きくすると、定常速度偏差は小さくできる。
・\(K , K_T\)の上限は、モデル化できていない機構部の共振や電気系の周波数特性などで決まる。
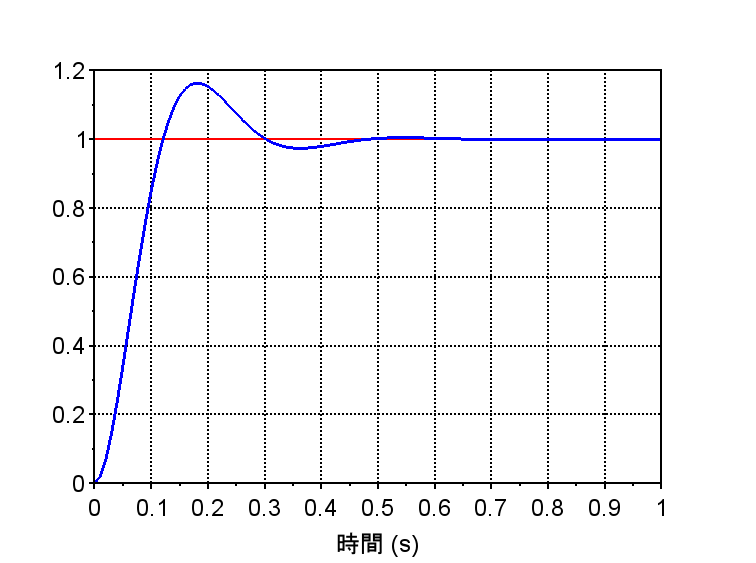
(定常位置偏差 評価)
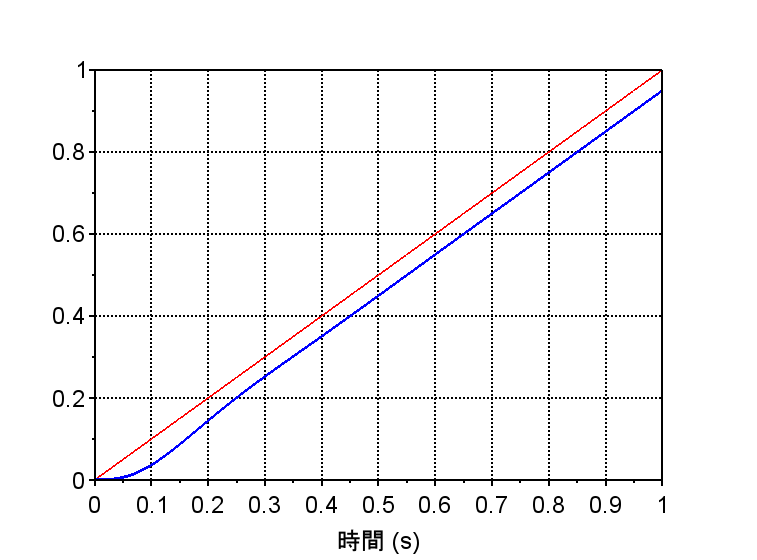
(定常速度偏差 評価)

