44. 周波数応答による補償器の設計事例
制御系を構成する場合、システム全体が望ましい特性をもつ(制御仕様を満足する)ように制御器(補償器)を設計することが必要である。ここでは、制御系設計用ソフトウェアScilabを用いて、種々の仕様に対する制御器の設計を周波数領域で行い、その制御性能を確認する方法を解説する。古典制御理論に基づいた設計例に関しては、「33. 制御系の設計例」で一通り解説しているが、設計手順などを含め少し詳しく解説する。
フィードバック制御系の制御特性(安定性、速応性)は、その概観を開ループ伝達関数\(L(s)\) の周波数応答(ボード線図)で判定できる。
開ループ伝達関数 \(L(s) = C(s)G_p(s)\) のボード線図(ゲイン曲線、位相曲線)は、\(C(s)\)のボード線図と\(G_p(s)\)のボード線図を合成したものになる。ここでは、フィードバック制御系が望ましい制御特性のボード線図になるように補償器\(C(s)\)を設計する方法を説明する。
補償器\(C(s)\)として、比例ゲイン\(K\) と位相進み要素、もしくは位相遅れ要素を用いる。比例ゲイン要素、位相進み要素、位相遅れ要素の3要素を全て組み合わせて使用することが望ましい場合も多いが、ここでは、比例ゲインのみ、比例ゲインと位相進み要素、比例ゲインと位相遅れ要素の3通りでの制御系設計を考える。
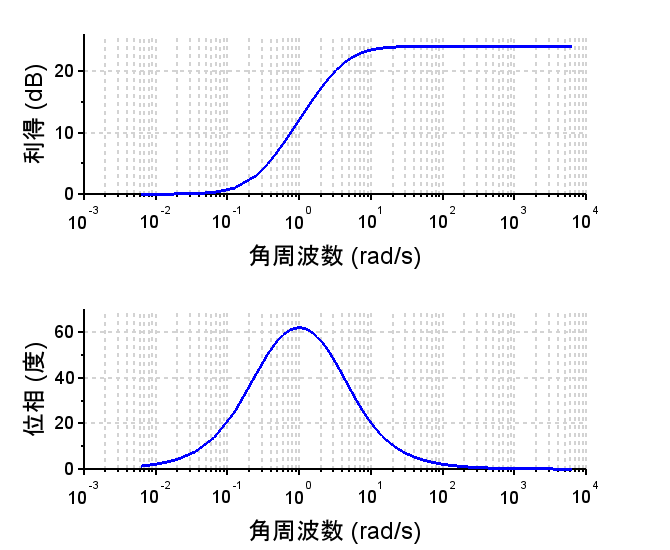
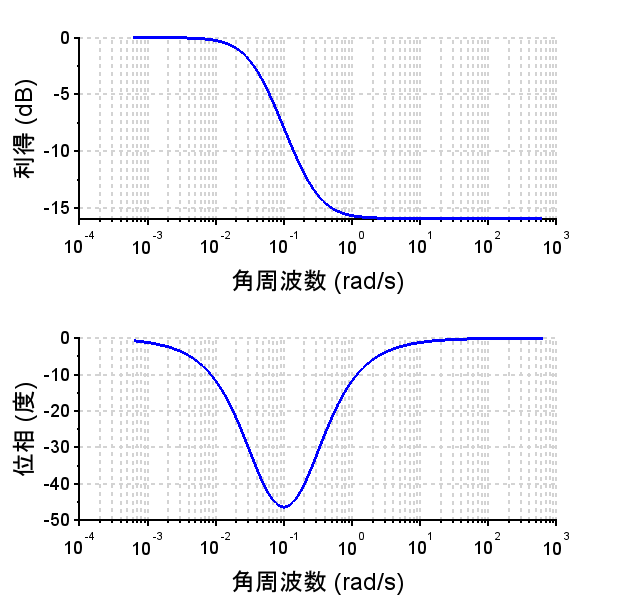
位相進み要素、及び位相遅れ要素の伝達関数は $$G_c(s) = \frac{1 + \alpha Ts}{1 + Ts}$$と表される。ただし、\(\alpha \gt 1\) のとき位相進み要素となり、\(0 \lt \alpha \lt 1\) のとき位相遅れ要素となる。
それぞれの要素の周波数特性は図のようになる。
位相進み要素の最大の位相進み角、位相遅れ要素の最大位相遅れ角をそれぞれ\(\phi_m\)とし、その時の角周波数を\(\omega_m\) [rad/s]とすると、$$\omega_m = \frac{1}{T\sqrt{\alpha}}$$ $$\sin{\phi_m }= \frac{\alpha - 1}{\alpha + 1}$$と表される。
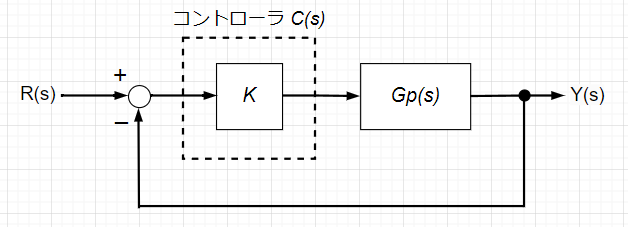
制御対象は、$$G_p(s)=\frac{4}{s(s+1)(s+2)}$$とする。
設計仕様:位相余裕 \(p_m=60\text{°}\)を満たすこと。
コントローラ:\(C(s)=K\)のみ使用。
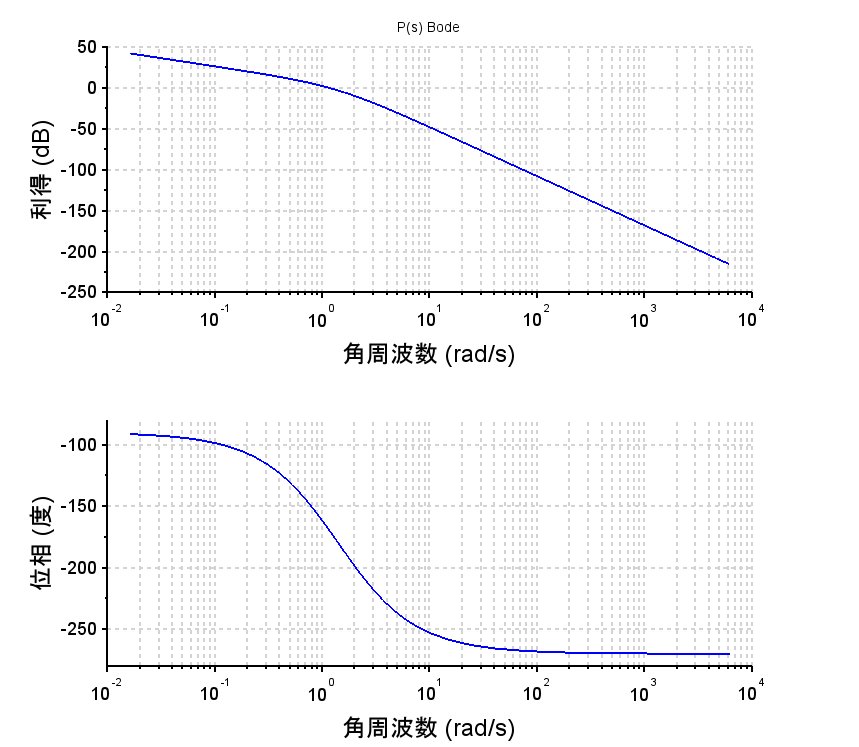
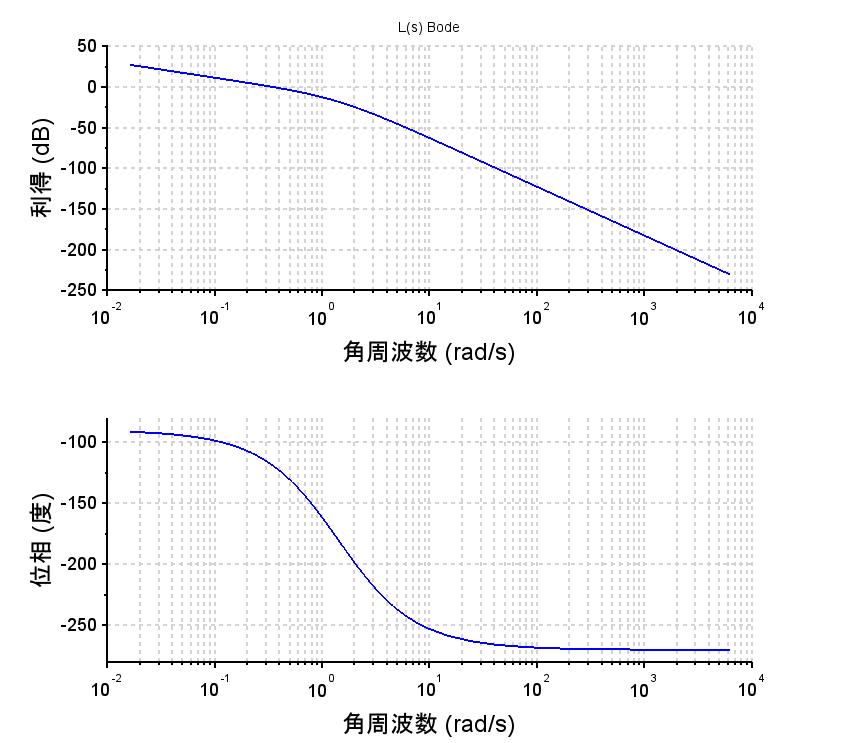
ゲイン\(K=0.19\)
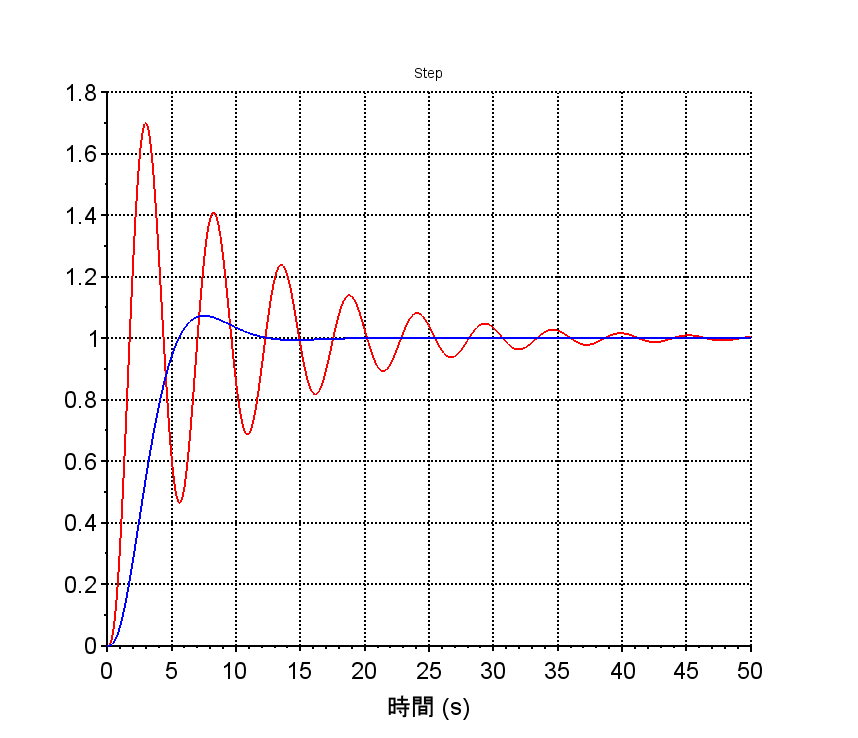
補償前(赤線)、補償後(青線)
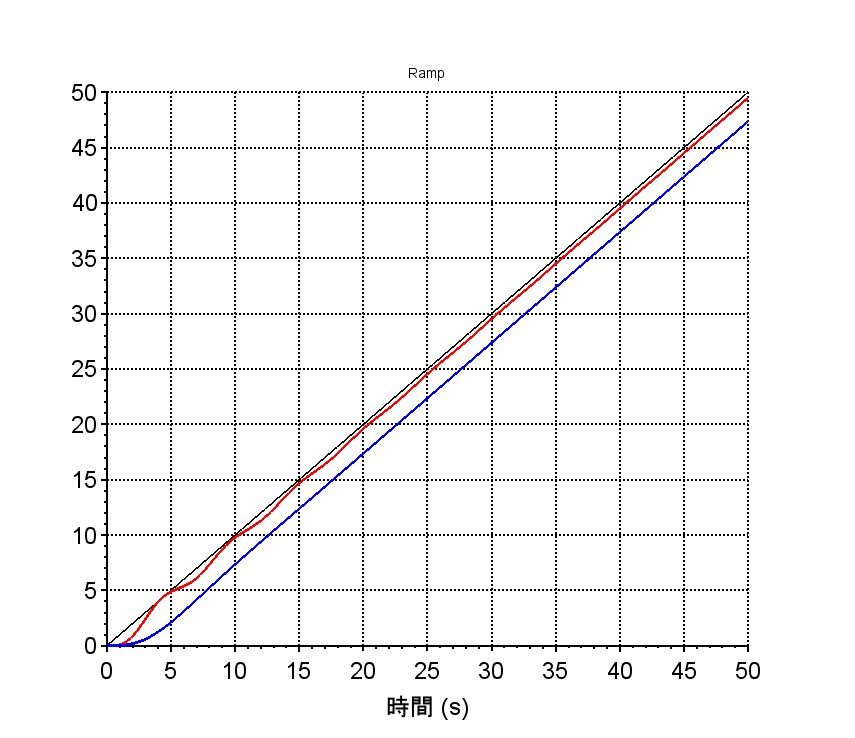
補償前(赤線)、補償後(青線)
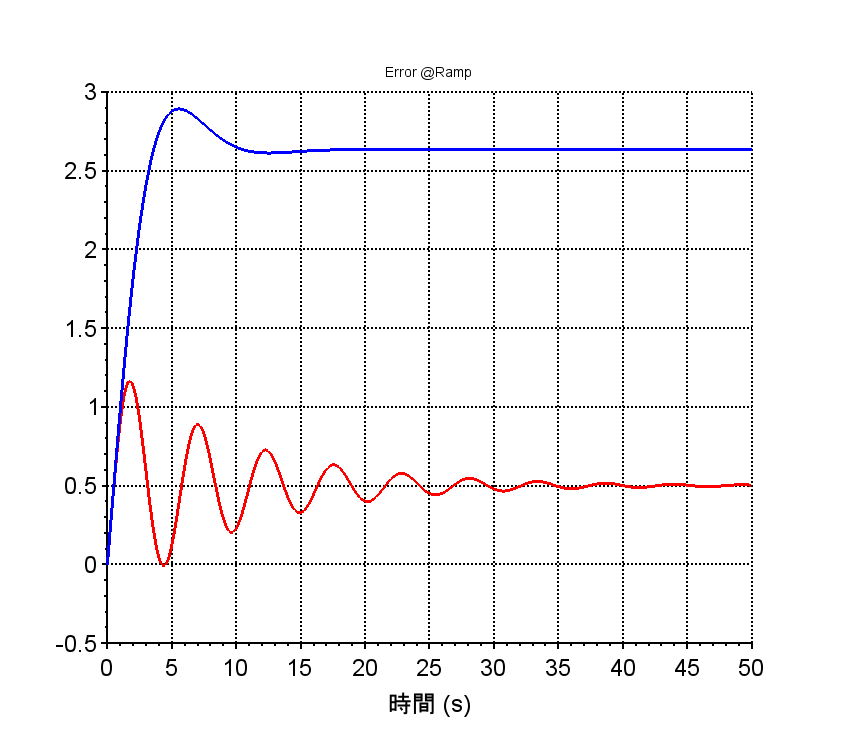
補償前(赤線)、補償後(青線)
ゲイン補償による制御
制御器\(C(s)\) に比例ゲインを用いてフィードバック制御系の特性改善を行う。
設計手順
(1)Scilabを使用して\(G_p(s)\)のボード線図を描く。
(2)ボード線図をもとに、仕様を満たすためのゲイン\(K\)を決定す
(3)Scilabを使用して、補償後の開ループ伝達関数\(L(s)\)のボード線図を描き、フィードバック制御系の位相余裕\(p_m\),ゲイン余裕\(g_m\)を求め、仕様を満たしているか確認する。
(4)Scilabを使用し、制御器を入れない場合(補償前)のフィードバック制御系を構成して時間応答波形を描く。
(5)Scilabを使用し、制御器を入れた場合(補償後)のフィードバック制御系を構成して時間応答波形を描く。
・\(G_p(s)\)のボード線図より、ゲイン補償器のゲインを\(K=0.2\)以下(\(-14dB\)以下)とする。(\(K=0.19\)に設定した。)
・開ループ\(L(s)\)のボード線図から位相余裕\(p_m=60.6\text{°}\)、ゲイン余裕\(g_m = 17.9dB\)とわかり、設計仕様を満たす。
・補償前(制御器を入れない場合)のフィードバック制御系のステップ応答(赤線)、補償後(制御器を入れた場合)のフィードバック制御系のステップ応答(青線)を見ると、補償前のステップ応答は大きく振動しており、安定性に欠け実用的でないことが分かる。補償前、補償後に関わらず、開ループ伝達関数が1型なので、定常位置偏差は0である。
・ランプ応答から定常速度偏差を見ると、補償前(赤線)、補償後(青線)を比較し、補償前の方が定常速度偏差は小さいが、目標信号との差(ランプ応答の偏差)を見ると補償前は振動的であり安定性に欠けることが分かる。補償後では、ゲインを下げて安定性を確保しているため、低域でのゲインが低下し、定常速度偏差が大きくなっている。
ゲイン補償 Scilabスクリプト
//ゲイン補償による制御性能の改善
//制御仕様 位相余裕:60度
clear;clf;
// Plant 制御対象
s=%s;
//制御対象の伝達関数
P = 4/(s*(s+1)*(s+2)); Ps=syslin('c',P); scf(0);
//制御対象のボード線図
bode(Ps, 10^-3, 10^3, "rad");xtitle('P(s) Bode');
//制御対象だけでの閉ループ伝達関数 T0
T0=P/(1+P); T0s=syslin('c',T0);
//Gain Compensator Pm=60° (設計仕様)
K=0.19;
//開ループ伝達関数 L
L=K*P; Ls=syslin('c',L);
//閉ループ伝達関数 T
T=L/(1+L); Ts=syslin('c',T); scf(1);
//開ループ伝達関数のボード線図
bode(Ls, 10^-3, 10^3, "rad");xtitle('L(s) Bode');
//位相余裕
pm=p_margin(Ls);
//利得余裕
gm=g_margin(Ls); scf(2);
//閉ループ伝達関数のボード線図
bode(Ts, 10^-3, 10^3, "rad");xtitle('T(s) Bode');
//Step response
t=0:0.1:50;
//T0の単位ステップ応答
y0=csim('step',t,T0s); scf(3);
plot2d(t,y0,5);xgrid;xtitle('Step');
//Tの単位ステップ応答
y=csim('step',t,Ts); plot2d(t,y,2);
//Ramp response
t=0:0.1:50; r=t;
//T0のランプ信号への応答
y0r=csim(r,t,T0s); scf(4); plot2d(t,r);plot2d(t,y0r,5);xgrid;xtitle('Ramp')
//Tのランプ信号への応答
yr=csim(r,t,Ts); plot2d(t,yr,2);
//T0のランプ信号応答の偏差
e0=r-y0r; scf(5); plot2d(t,e0,5);xgrid;xtitle('Error @Ramp');
//Tのランプ信号応答の偏差
e=r-yr; plot2d(t,e,2);
位相進み補償による制御
設計仕様:ゲイン交差周波数 \(f_g=0.4\)[Hz]
\(\omega_g=2.5\)[rad/s]
位相余裕 \(p_m=40\text{°}\)を満たすこと。
コントローラ:位相進み要素を使用。\(C(s)=KG_c(s)=K\frac{1 + \alpha Ts}{1 + Ts}\)
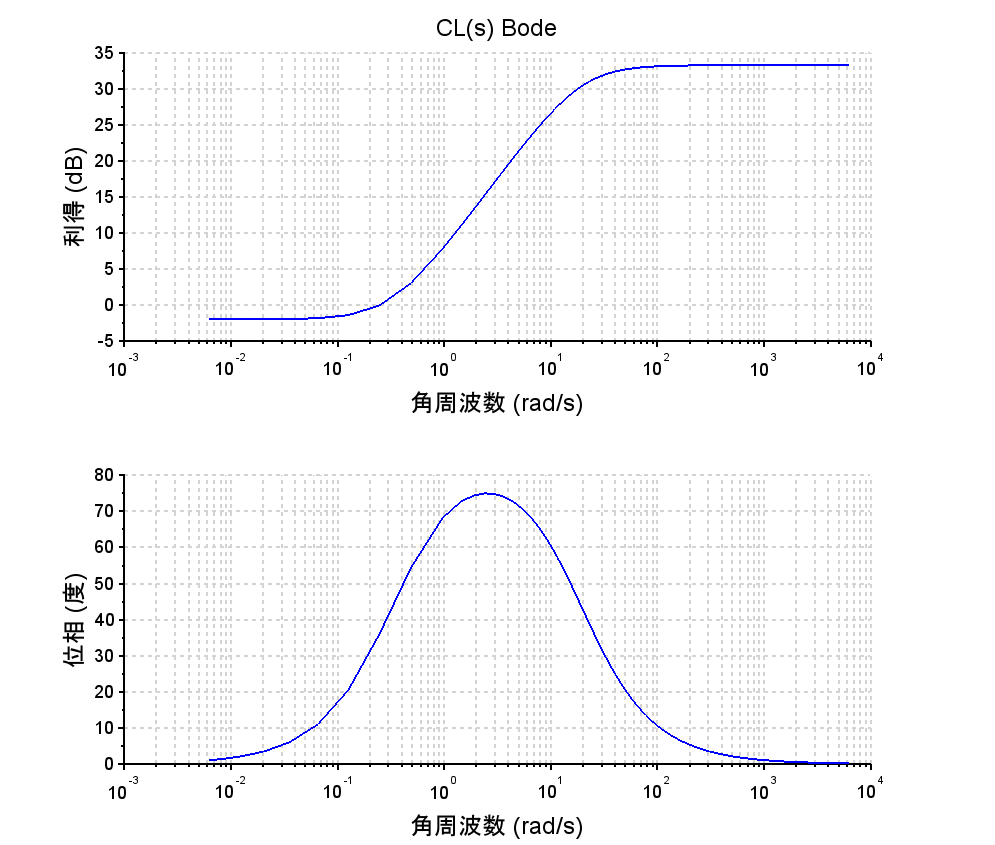
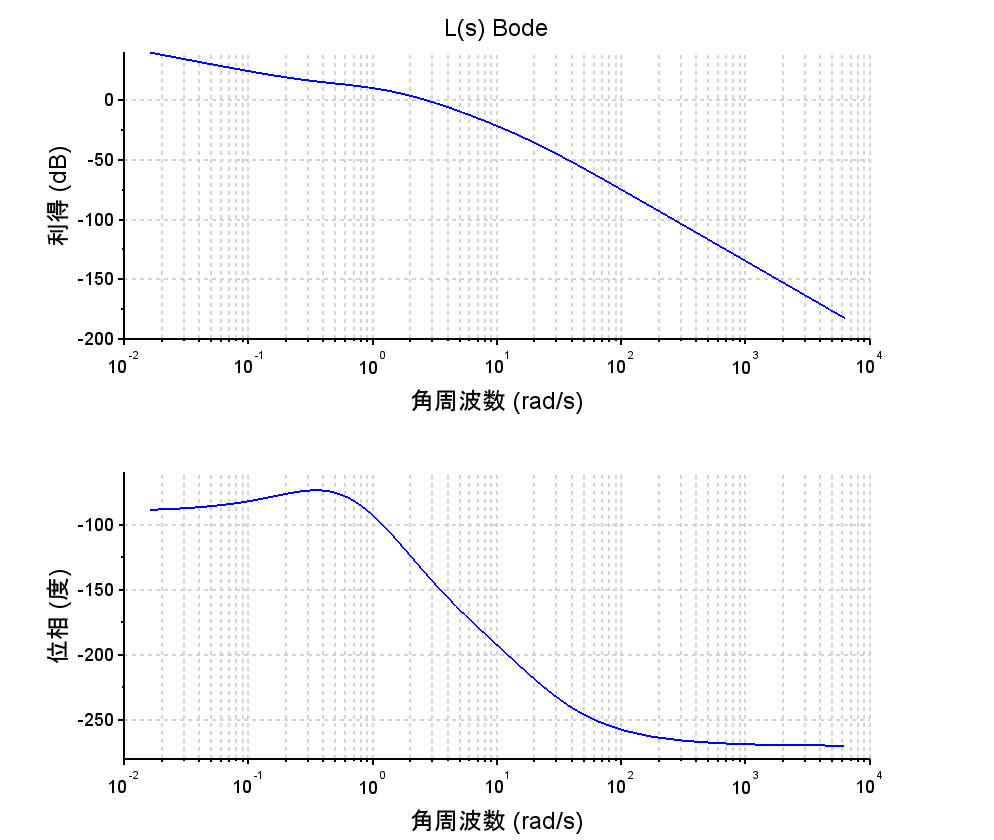
コントローラ\(C(s)\)に比例ゲイン\(K\)と位相進み要素 を用いて制御系の補償(特性改善)を行う。
設計手順
(1) \(G_p(s)\)のボード線図を描く。
(2) 望みの位相余裕\(p_m\)を与えるための最大位相進み角\(\phi_m\)を決める。
(最終的に\(\omega_g\) がゲイン交差周波数になるため、\(\omega = \omega_g\)でゲインが0[dB]になると仮定)
(3) (2)の\(\phi_m\)になるよう位相進み要素のパラメータ\(\alpha\) と\(T\)を求め、位相進み要素の伝達関数\(G_c(s)\)を決定する。このときは、\(\omega_g\) の位相を\(\phi_m\)進めるので、\(\omega_m = \omega_g\) とする。
(4) \(L(s)=G_c(s)G_p(s)\)のボード線図を描く。
(5)\(\omega_g\)がゲイン交点周波数になるように(\(\omega = \omega_g\)で 0[dB] になるよう)\(K\) を決定。
(6)開ループ伝達関数\(L(s)=C(s)G_p(s)=KG_c(s)G_p(s)\)のボード線図を描き、仕様を満たしているか確認する。仕様を満足していない時は、\(\phi_m\)を変更(位相進み要素のパラメータ、\(\alpha\) と\(T\)を調整) して(2)以下を繰り返す。
(7)補償後の位相余裕、ゲイン余裕を求める。
(8)コントローラを入れた時(補償後)のフィードバック制御系を構成し、時間応答波形を描く。
・位相進み要素は、ゲイン交差周波数(\(2.5\)[rad/s])近傍において、最大位相進み角\(\phi_m\)を\(75\text{°}\)となるように設計した。
・設計値として、位相進み補償のパラメータを\(K=0.8\)、\(a= 57.7\)、\(T=0.05\)とした。
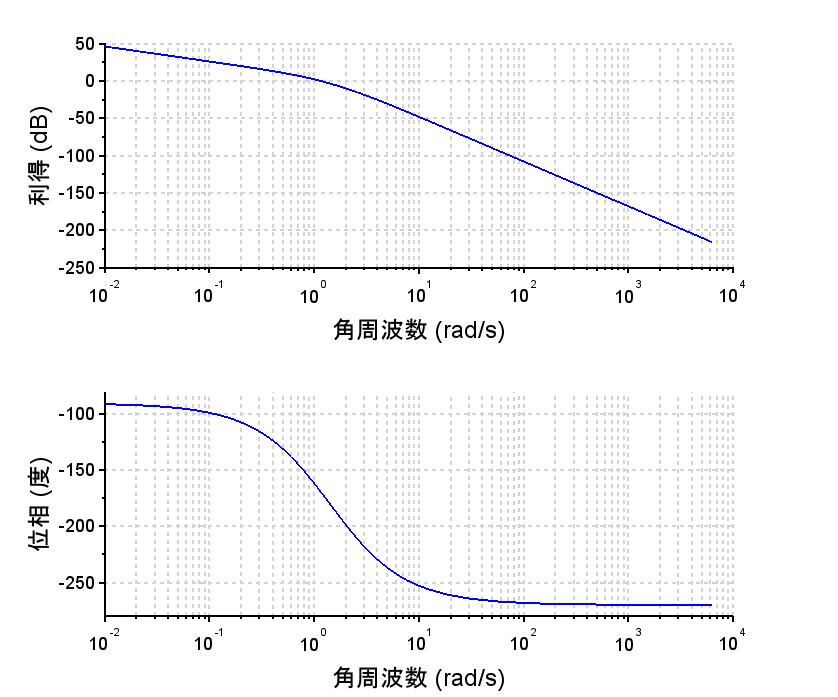
・開ループ周波数応答より、ゲイン交差周波数\(2.5\)[rad/s]で位相余裕\(p_m=41.9\text{°}\)、ゲイン余裕\(g_m = 15.6dB\)で、制御仕様を満たす。
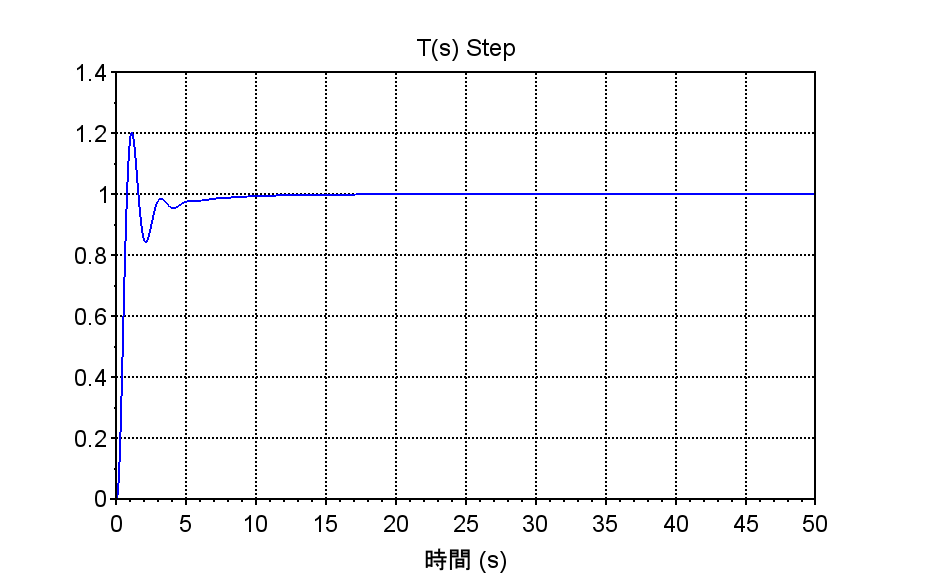
・ステップ応答をみると制御帯域が高くなったことにより、立ち上がり時間が短くなり、速く整定している。行き過ぎ量は1.2程度なので、一般的には許容できる。
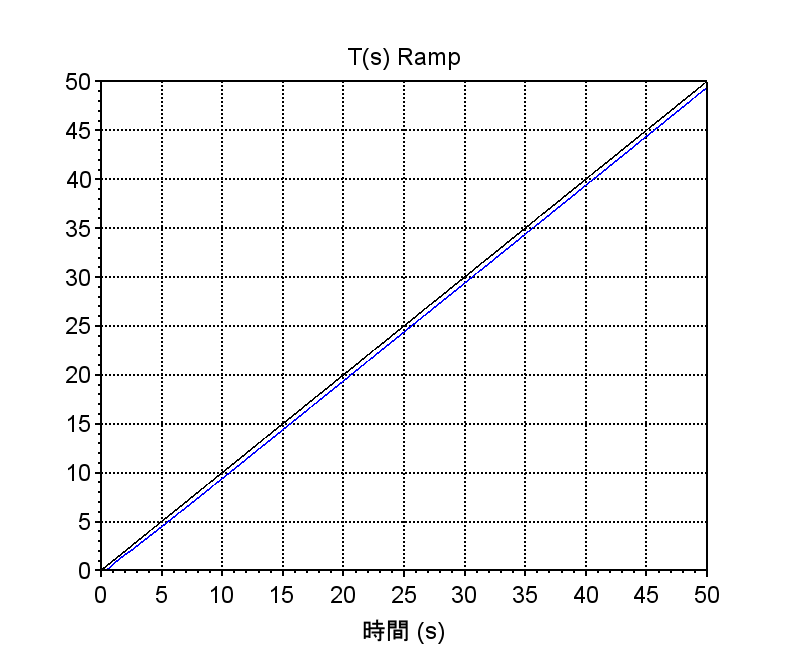
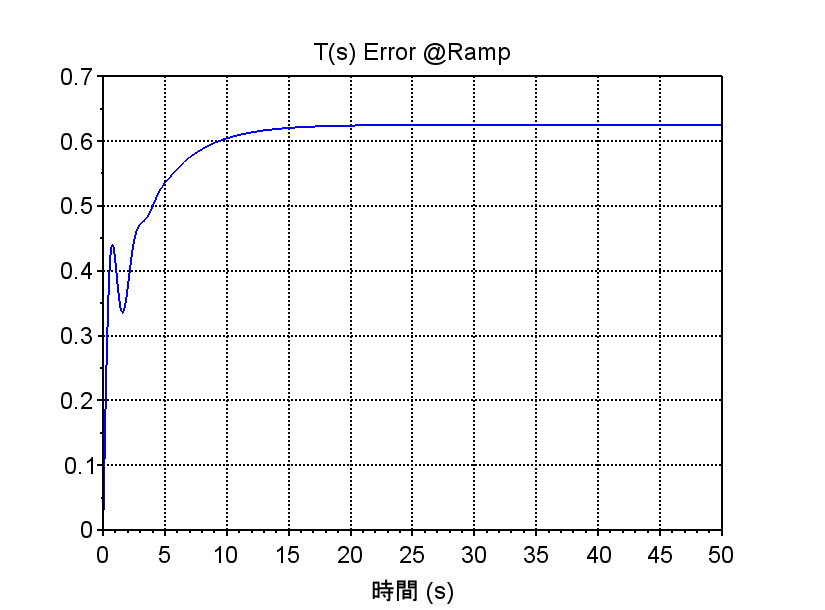
・ランプ応答の偏差をみると応答特性は安定しているが、定常速度偏差が\(0.6\)以上ある。ゲイン補償の場合に比較して、制御帯域が高くなり、低域のゲインが上がったため定常速度偏差は小さくはなっている。さらに定常速度偏差を抑圧するためには、低域のゲインを高くする積分補償や位相遅れ補償が必要である。
位相進み補償 Scilabスクリプト
//位相進み補償による制御性能の改善
//制御仕様
//ゲイン交差周波数:0.4Hz(2.5rad/s) 位相余裕:40度
clf;clear;
// Plant
s=%s;
P = 4/(s*(s+1)*(s+2));
//Plant Transfer Function
Ps=syslin('c', P);
//設計仕様 fg=0.4[Hz]、位相余裕40度、
//Lead Compensator
K=0.8; //Gain
fg=0.4; //ゲイン交差周波数 0.4[Hz]
Lead=(75*%pi)/180; //最大位相進み角75°
wg=2*%pi*fg;
a=(1+sin(Lead))/(1-sin(Lead));
Tc=1/(sqrt(a)*wg);
CL=K*(1+a*Tc*s)/(1+Tc*s);
CLs=syslin('c',CL);
scf(0); bode(CLs, 10^-3, 10^3, "rad"); xtitle('CL(s) Bode');
L=CL*P; //Loop Transfer Function
T=L/(1+L); //Feedback Transfer Function
Ls=syslin('c',L);
Ts=syslin('c',T);
scf(1); bode(Ls, 10^-3, 10^3, "rad"); xtitle('L(s) Bode')
phm=p_margin(Ls);
gm=g_margin(Ls);
scf(2); bode(Ts, 10^-3, 10^3, "rad"); xtitle('T(s) Bode');
//Step response
scf(3);
t=0:0.1:50;
y=csim('step',t,Ts);
plot(t,y);xgrid; xtitle('T(s) Step');
//Ramp response
scf(4);
t=0:0.1:50;
r=t;
y=csim(r,t,Ts);
plot(t,r);plot(t,y);xgrid; xtitle('T(s) Ramp');
e=r-y;
scf(5); plot(t,e);xgrid; xtitle('T(s) Error @Ramp');
位相遅れ補償による制御
設計仕様:定常速度偏差 \(e_v (\infty)=1/10 \) 位相余裕 \(p_m=40\text{°}\)を満たすこと。
コントローラ:位相遅れ要素を使用。\(C(s)=KG_c(s)=K\frac{1 + \alpha Ts}{1 + Ts}\)
コントローラ\(C(s)\)に比例ゲイン\(K\)と位相遅れ要素\(G_c(s)\)を用いて制御系の補償(特性改善)を行う。
設計手順
(1)定常特性を満たすようにゲイン\(K\) を決定する。
(2) \(L(s)=KG_p(s)\)のボード線図を描く。
(3)仕様の位相余裕を与える点の角周波数\(\omega_g\) を読みとる。
(4) \(\omega = \omega_g\)の点がゲイン交差周波数になるように、位相遅れ要素を用いてゲイン曲線を下げる。そのための位相遅れ要素の係数\(\alpha\)と\(T\)を決定する。
(5)開ループ伝達関数 のボード線図を描く。
(6)仕様が満たされているかを調べる。満たされていないときは、\(\omega_g\)の値を少し変更して(3)以下を繰り返す。
(7)補償後の位相余裕、ゲイン余裕を求める。
(8)コントローラを入れた時(補償後)のフィードバック制御系を構成し、時間応答波形 を描く。
(9)速度偏差の応答をグラフに描き、定常速度偏差の値を確認する。
※位相遅れ要素は、\( \omega \gt \frac{1}{\alpha T}\)の領域のゲインを \(20\log\alpha\)[dB] 下げる働きがある。
角周波数\(\omega_g\) のゲインを \(20\log\alpha\) [dB] 下げるためには、\(\omega_g\)を\(G_c(s)\) の折点角周波数\(\frac{1}{\alpha T}\)よりも十分大きく( \(\omega_g \gg \frac{1}{\alpha T} \) )にとる必要がある。そうしない場合、位相遅れ要素による位相遅れの影響を受け、\(\omega_g\) での位相が変化してしまい調整が難しくなる。通常\(\omega_g\)を\(\frac{1}{\alpha T}\) から1~2デカード (10倍~ 100倍) 離すとよい。
・定常速度偏差\(e_v\)は、「27.定常特性と内部モデル原理」より、$$e_v=\lim_{s \rightarrow 0} \frac{1}{sL(s)}=\lim_{s \rightarrow 0} \frac{1}{K\frac{4}{(s+1)(s+2)}}=0.1$$を満たす必要があるので、\(K \ge 5\)が条件となる。また、位相遅れ補償のパラメータは\(\alpha \lt 0.2\)である。
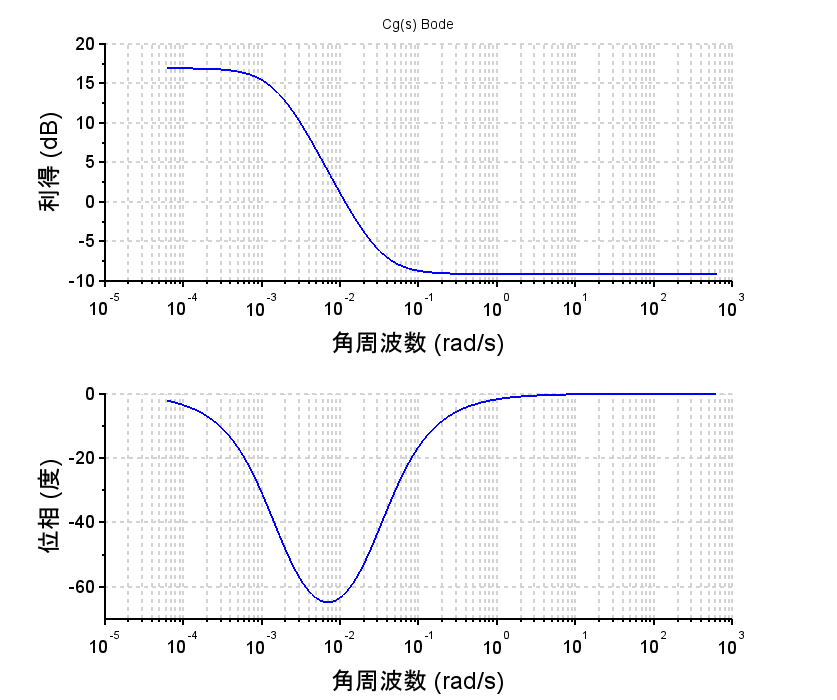
・設計値として、位相遅れ補償のパラメータを\(K=7.0\)、\(a=0.05\)、\(T=636.6\)とした。
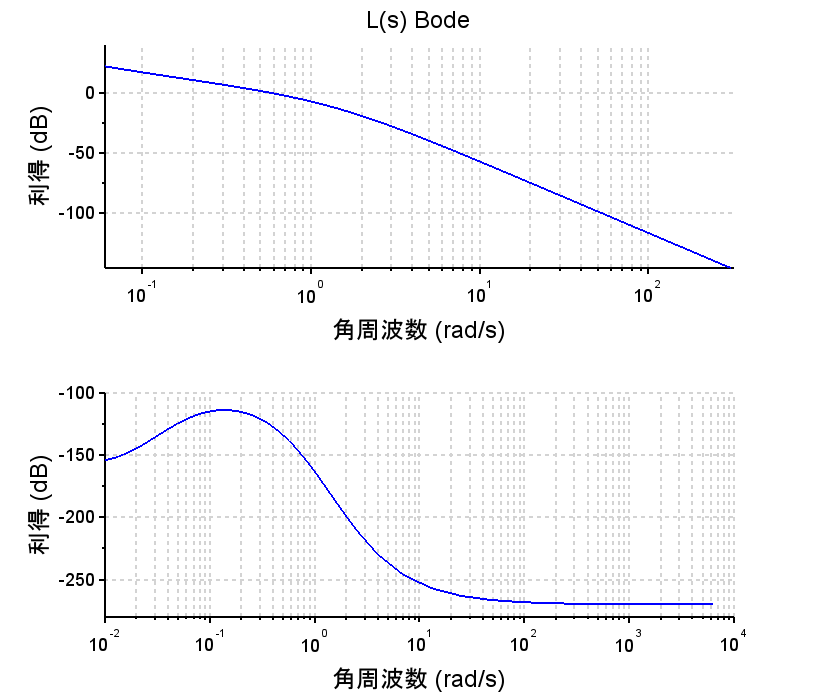
・開ループ周波数応答より、ゲイン交差周波数\(0.57\)[rad/s]で位相余裕\(p_m=40.7\text{°}\)、ゲイン余裕\(g_m = 12.2dB\)で、制御仕様を満たす。
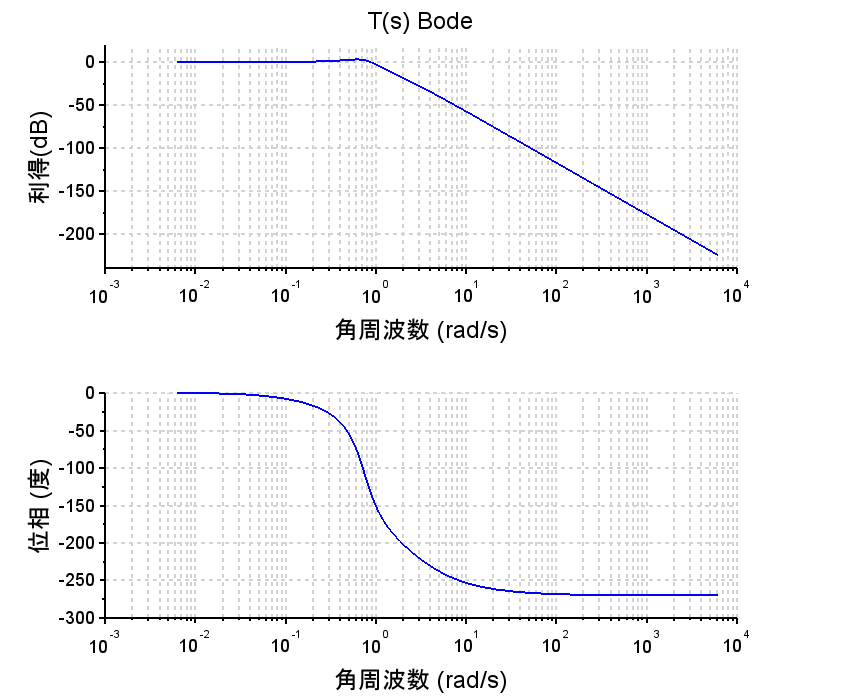
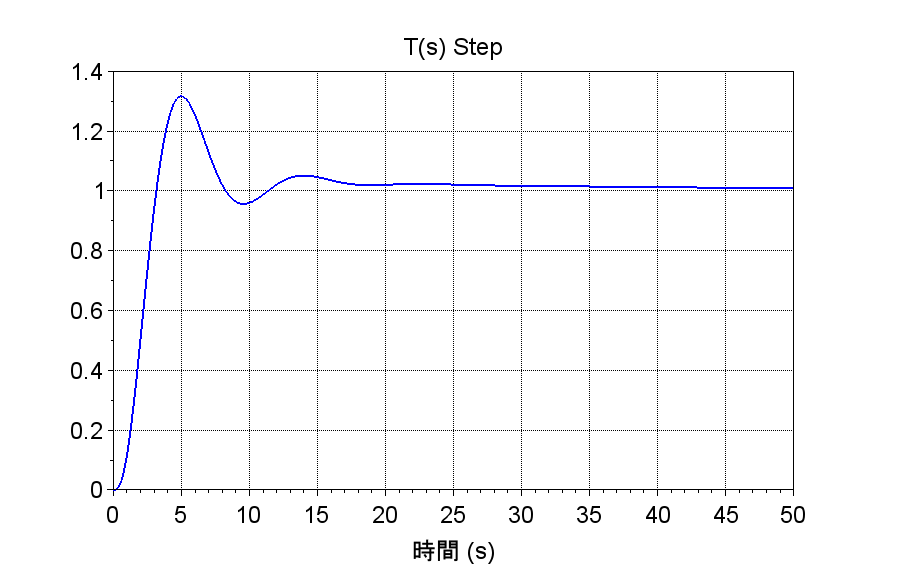
・ステップ応答は、位相進み要素を使用した場合に比較して立ち上がり特性が悪い。これは、位相余裕を確保するために制御帯域を低くしていることによる。\(L(s)\)が1型であるため定常位置偏差は0である。立ち上がり特性を改善するには、位相進み要素が必要であるが、これは制御で求める性能による。制御帯域を上げることは一般に耐雑音性が劣化することになるので注意が必要である。
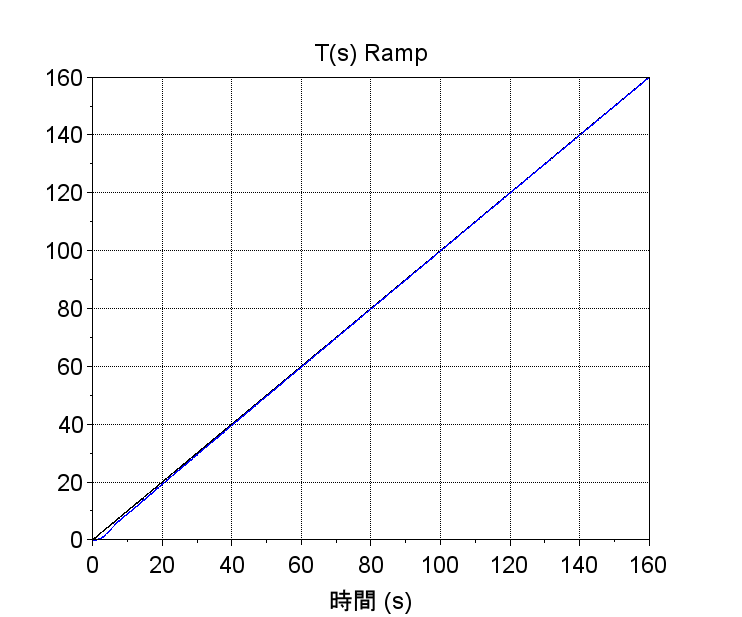
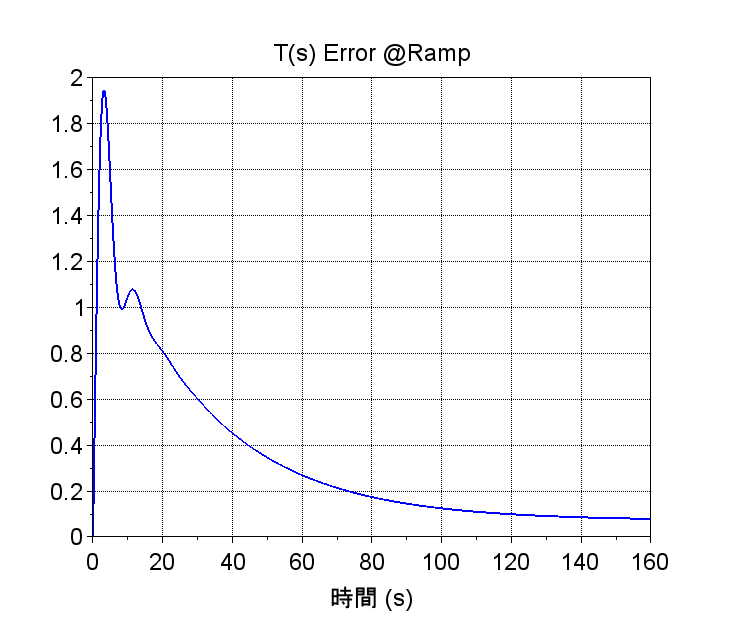
・ランプ応答、ランプ応答の偏差をみると定常速度偏差\(e_v(\infty)\)が1/10以下になっており、制御仕様を満たしている。ただし、ステップ応答と同様に偏差が十分に小さくなるのに時間がかかっており、速応性は検討が必要である。
位相遅れ補償 Scilabスクリプト
//位相遅れ補償による制御性能の改善
//P=4/(s(s+1)(s+2))
//制御仕様
//定常速度偏差:1/10,位相余裕:40度
clf; clear;
// Plant
s=%s;
P=4/(s*(s+1)*(s+2)); //Plant Transfer Function
Ps=syslin('c', P);
scf(0); bode(Ps, 10^-5, 10^3, "rad");
//Lag Compensator ev=0.1, Pm=40°
K=7.0;
fg=0.1;
wg=2*%pi*fg;
Tga=20/wg; //wgでの位相遅れが影響しないようにwgから十分離す
a=0.05;
Tg=Tga/a;
Cg=K*(1+a*Tg*s)/(1+Tg*s);
sCg=syslin('c',Cg);
scf(1); bode(sCg, 10^-5, 10^2, "rad"); xtitle('Cg(s) Bode');
L=Cg*P; //Loop Transfer Function
Ls=syslin('c',L);
T=L/(1+L); //Feedback Transfer Function
Ts=syslin('c',T);
scf(2); bode(Ls, 10^-5, 10^3, "rad"); xtitle('L(s) Bode');
phm=p_margin(Ls);
gm=g_margin(Ls);
scf(3); bode(Ts, 10^-3, 10^3, "rad"); xtitle('T(s) Bode');
//Step response
scf(4);
t=0:0.1:50;
y=csim('step',t,Ts);
plot(t,y);xgrid; xtitle('T(s) Step');
//Ramp response
scf(5);
t=0:0.1:160;
r=t;
y=csim(r,t,Ts);
plot(t,r);plot(t,y);xgrid; xtitle('T(s) Ramp');
e=r-y;
scf(6);
plot(t,e);xgrid; xtitle('T(s) Error @Ramp');

