10. ブロック線図

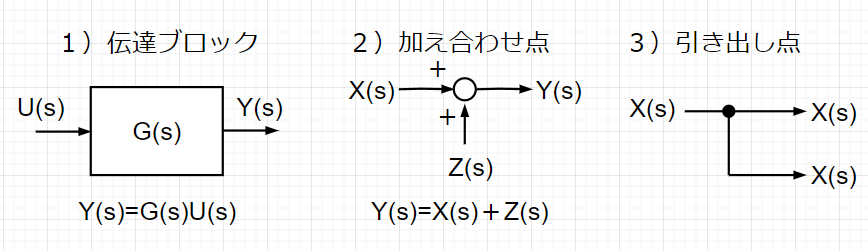
伝達ブロックの結合法

3種類の伝達ブロックの結合法を使うことで、様々な制御システムを表現することができる。ここでは、結合を主体に説明しているが、制御システムの内部構造を細かく見る場合には、逆の分解を使用した方が良いこともある。また、実践的には結合する場合は、制御要素ごとの特性に応じた結合条件を考慮しなければならないことに注意されたい。

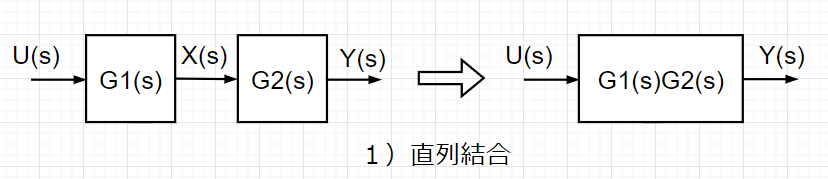
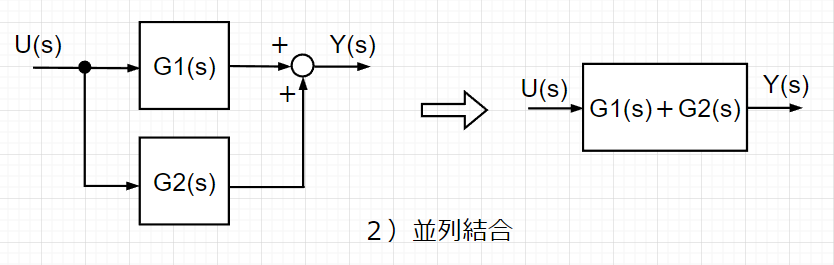
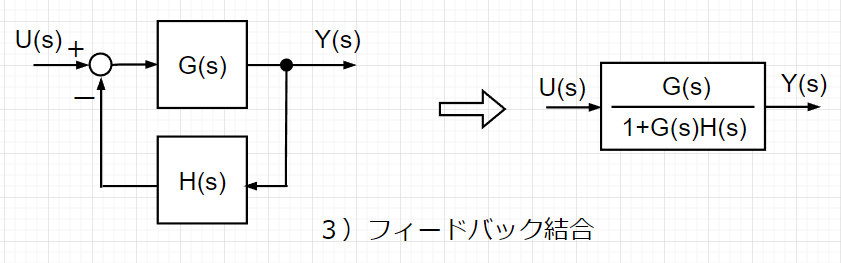
ブロック線図から伝達関数を求める手順

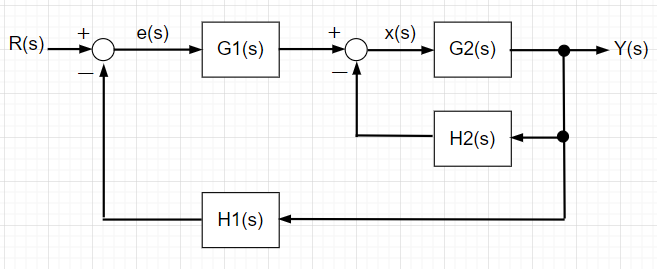
\(e(s)=R(s)-H1(s)Y(s)\)　,　\(x(s)=G1(s)e(s)-H2(s)Y(s)\)
\(Y(s)=G2(s)x(s)\) なので、\(x(s),e(s)\) を代入して整理すると、$$Y(s)=G2(s)[G1(s)\{R(s)-H1(s)Y(s)\}$$ $$-H2(s)Y(s)]$$ $$\{1+G2(s)G1(s)H1(s)+G2(s)H2(s)\}Y(s)$$ $$=G2(s)G1(s)R(s)$$ よって、入力\(R(s)\)から出力\(Y(s)\)までの伝達関数\(T(s)\)は、$$T(s)=\frac{Y(s)}{R(s)}$$ $$=\frac{G2(s)G1(s)}{1+G2(s)G1(s)H1(s)+G2(s)H2(s)}$$となる。
このように、ブロック線図において中間変数\(e(s) , x(s)\)を設定することで見通しを良くして信号間の演算を記述することで、ブロック線図から代数演算によって任意の信号間の伝達関数を求めることができる。（この図の場合、\(e(s)\)は偏差、\(x(s)\)は操作量と考えることもできる。）