4. 状態変数線図
制御システムは、ラプラス変換で表示したブロック線図を使って表記することが多い。このブロック線図を状態方程式に合わせて、状態変数を中心に描いたものが状態変数線図である。
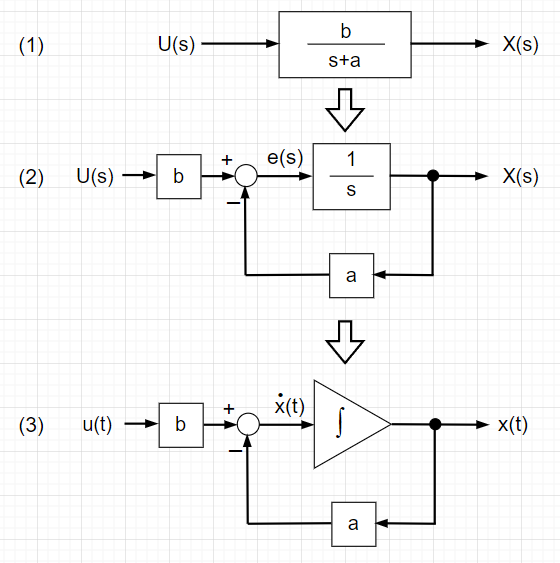
ブロック線図の(1)は、入力信号\(U(s)\)がシステム\(\frac{b}{s+a}\)に入力され、出力信号\(X(s)\)が得られることを表しており、\(G(s)=\frac{X(s)}{U(s)}\)を伝達関数と呼ぶ。この図(1)は図(2)のように書き換えることが可能である。図(2)で、$$e(s)=bU(s)-aX(s) \;\;\;\; X(s)=e(s)\frac{1}{s}$$よって、$$sX(s)=bU(s)-aX(s) \;\;\;\; (s+a)X(s)=bU(s)$$よって、$$\frac{X(s)}{U(s)}=\frac{b}{s+a}$$となり、図(1)と図(2)が等価であることが分かる。さらに、\(\frac{1}{s}\)は積分作用のラプラス変換を表しているので、時間領域では、時間積分\(\int dt \)と表せる。よって、\(s\)領域の図(2)を時間領域に書き換えると図(3)となる。この線図を状態変数線図と呼ぶ。このとき、積分器の入力は\(\dot{x}(t)\)と表せる。従って、この図から状態方程式、$$\dot{x}(t)=-ax(t) + bu(t)$$が得られる。多くのブロックがある場合は、各ブロックを時間領域に変換して、状態方程式にまとめればよい。この場合、状態変数の数は積分器の数となる。
状態変数線図の例
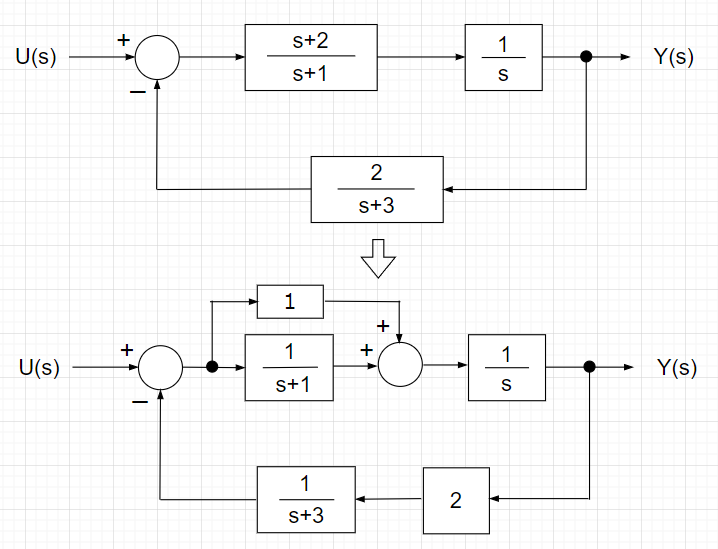
次の伝達関数$$G(s)=\frac{s+2}{s+1} \cdot \frac{1}{s}$$と$$H(s)=\frac{2}{s+3}$$によるフィードバック制御系の状態変数線図を考える。
「伝達関数によるブロック線図」に示すように\(\frac{s+2}{s+1}\)は、\(1 + \frac{1}{s+1}\)に変形できる。また、\(\frac{2}{s+3}\)は\(2\)と\(\frac{1}{s+3}\)と分解できる。
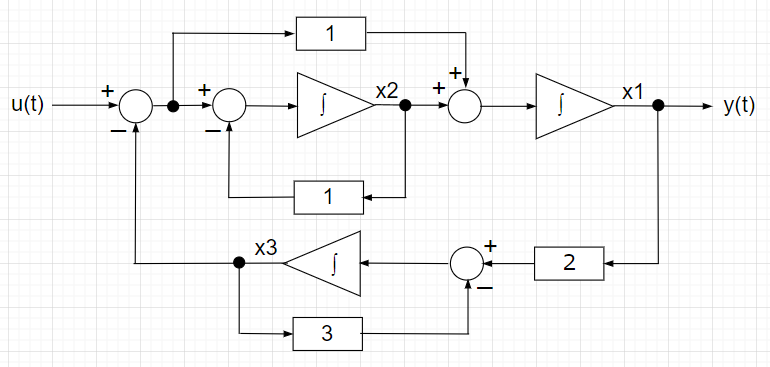
\(\frac{1}{s+1}\)や\(\frac{1}{s+3}\)は積分器とフィードバックで記述できるので、「状態変数線図の例」のように時間領域での状態変数線図で表現できる。この状態線図より、
状態方程式:$$\begin{bmatrix} \dot{x_1}(t) \\ \dot{x_2}(t) \\ \dot{x_3}(t) \end{bmatrix} = \begin{bmatrix} 0 & 1 & -1 \\ 0 & -1 & -1 \\ 2 & 0 & -3 \end{bmatrix} \begin{bmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \end{bmatrix} + \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} u(t)$$ 出力方程式:$$y(t) = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \end{bmatrix} $$となることがよくわかる。

