6. システムの安定性
線形時不変の自由システム$$\boldsymbol{\dot{x}}(t) = \boldsymbol{Ax}(t) \;\;\;\; \cdots (1)$$において、全ての初期ベクトル\(\boldsymbol{X}(0)\)に対して$$\lim_{t \rightarrow \infty} \boldsymbol{x}(t) = 0$$となるとき、漸近安定という。(\(\boldsymbol{x}(t)\):状態変数ベクトル、\(\boldsymbol{A}\):システム行列)
漸近安定のための必要十分条件は、\(\boldsymbol{A}\)のすべての固有値の実部が負、\( Re\{\lambda_i(\boldsymbol{A})\} \lt 0 \;\;\;\; (\forall i)\) である。
漸近安定の条件について
状態方程式\((1)\)式において、\(\boldsymbol{A}\)の固有値\(\lambda_i\)を求める。固有値 \(\lambda_i\) は、固有ベクトル\(\boldsymbol{v}_i\) が存在する場合に、\(\boldsymbol{Av}_i = \lambda_i \boldsymbol{v}_i \)となる。従って、$$det(\boldsymbol{A} - \lambda_i \boldsymbol{I}) = 0$$となる(\(\boldsymbol{I}\)は単位行列)。固有値\(\lambda_i\) の実部が負である場合、指数関数の形で表される解は\(x(t) = e^{\lambda_i t} v_i\)となる。任意の初期値\( x(0)\) が与えられた場合、状態変数\(x(t)\) は、$$x(t) = \sum_{i=1}^n c_i e^{\lambda_i t} v_i$$で表される。\(c_i\)は初期値\(x(0)\)と固有ベクトル\(v_i\)の内積を表す。固有値\(\lambda_i\) の実部が負であるため、指数関数 \(e^{\lambda_i t}\)は時間が経過するにつれて\(0\)に近づく。したがって、時間が十分に経過すれば、各項の寄与は非常に小さくなり、状態変数 \(x(t)\) は収束する。これにより、初期値 \(x(0)\) が任意の値でも、時間が経過するにつれて系の状態が収束する。
\((1)\)式の自由システムにおいて、\(Re\{\lambda_i\} \gt 0\)の固有値があると、ある\(\boldsymbol{x}(0)\)に対して\(||\boldsymbol{x}(t)|| \rightarrow \infty \;\; (t \rightarrow \infty )\)となる。また、\(Re\{\lambda_i\} = 0\)の固有値があると、持続振動となったり、\(\boldsymbol{x}(t) \rightarrow\)一定\((t \rightarrow \infty)\)となったりする。
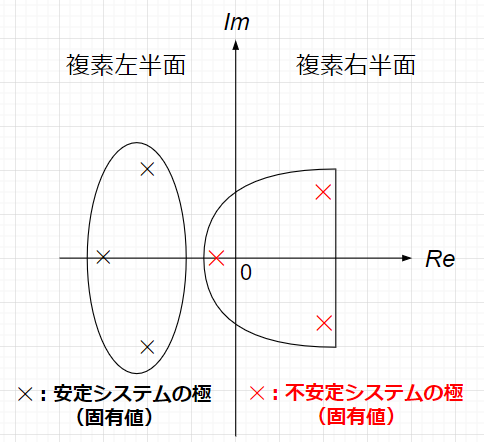
極とシステムの応答【例】
$$\boldsymbol{\dot{x}}(t) =\begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \boldsymbol{x}(t)$$ のインパルス応答を求める。システム行列(\(A\)行列)の固有値は、\([\lambda_1 , \lambda_2] = [j, -j]\)である。
*Scilab スクリプト
//極が虚軸上の[\(j,-j\)]の場合のインパルス応答
clear; clf;
A=[0 1 ;-1 0]; b=[1 ; 1]; c=[1 0;0 1];
G=syslin('c',A,b,c);
poles=spec(A); /* 固有値(極)の計算*/
//インパルス応答
t=0:0.1:20;
y = csim('impulse',t,G); scf(0); plot(t',y');
固有値(極)が虚軸上の \([j, -j]\)であるため、システムは不安定であり、インパルスを入力したときの状態変数\(\boldsymbol{x}(t)\)は持続振動となる。
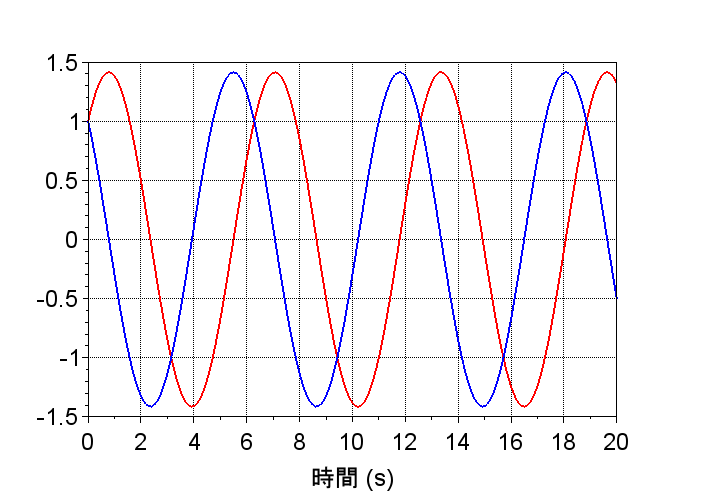
状態変数\(x_1,x_2\)のインパルス応答
$$\boldsymbol{\dot{x}}(t) =\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \boldsymbol{x}(t)$$ のインパルス応答を求める。システム行列(\(A\)行列)の固有値は、\([\lambda_1 , \lambda_2] = [j, j]\)である。
*Scilab スクリプト
//極が虚軸上の[\(j,j\)]の場合のインパルス応答
clear; clf;
A=[0 1 ;0 0]; b=[1 ; 1]; c=[1 0;0 1];
G=syslin('c',A,b,c);
poles=spec(A); /* 固有値(極)の計算*/
//インパルス応答
t=0:0.1:20;
y = csim('impulse',t,G); scf(0); plot(t',y');
固有値(極)が虚軸上の \([j, j]\)であるため、システムは不安定であり、インパルスを入力したときの状態変数\(\boldsymbol{x}(t)\)は定常値と発散値となる。
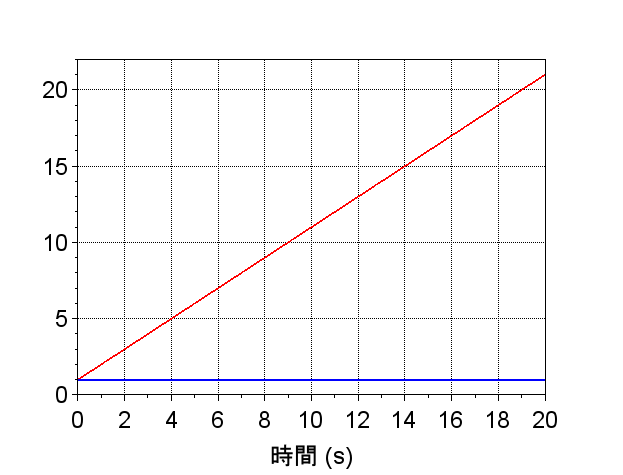
状態変数\(x_1,x_2\)のインパルス応答


“6. システムの安定性” に対して1件のコメントがあります。
コメントは受け付けていません。